Représenter les points caractéristiques :

1.  Schématiser une lentille convergente et son axe optique.

Placer le centre optique O de cette lentille.

2.  Placer sur le schéma les foyers objet F et image F’ sachant que la distance focale f’ = 5 cm.

Représenter les points caractéristiques :

1.  Schéma d’une lentille convergente avec le centre optique O et l’axe optique Δ.

2.  Schéma avec les foyers objet F et image F’ sachant que la distance focale f’ = 5 cm.

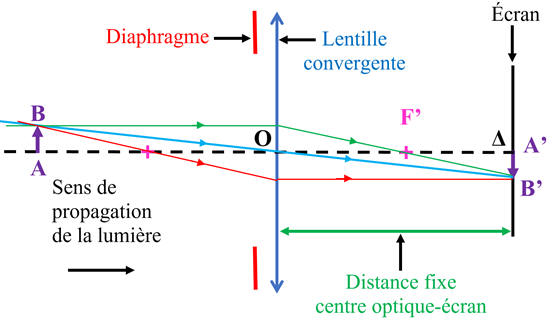
Comprendre la construction d’une image :

Sur le schéma ci-dessous, A’B’ est l’image d’un objet AB obtenue à travers une lentille mince convergente.

1.  Donner les propriétés des trois rayons ayant permis de construire l’image A’B’.

2.  Décrire l’image A’B’.

Comprendre la construction d’une image :

Schéma :

1.  Propriétés des trois rayons ayant permis de construire l’image A’B’.

-  Rayon 1 : issu du point B et passant par le centre optique : il n’est pas dévié.

-  Rayon 2 : issu du point B et parallèle à l’axe optique.

- Il émerge de la lentille en passant par le point F’ foyer - image.

-  Rayon 3 : issu du point B et passant par F (foyer - objet).

- Il émerge de la lentille parallèlement à l’axe optique.

2.  Décrire l’image A’B’.

-  L’image est réelle, renversée et plus petite que l’objet.

Construire une image :

Reproduire le schéma suivant, puis construire l’image A’B’ de l’objet AB.

Le grandissement :

Le schéma ci-dessous donne la représentation d’un objet AB et de son image A’B’ par une lentille convergente.

Schéma :

1.  Exprimer la valeur absolue du grandissement à l’aide des notations du schéma.

2.  Déterminer par deux calculs différents la valeur absolue du grandissement dans cette situation.

Le projecteur de diapositives :

Avant l’invention du vidéoprojecteur, on utilisait un projecteur de diapositives pour observer des images de grandes dimensions sur un écran.

Cet appareil comprend une source de lumière puissante qui éclaire une diapositive (photographie pouvant être traversée par la lumière) et une lentille convergente.

Une diapositive de dimension 24 mm × 36 mm est placée à 8,0 cm du centre de la lentille mince convergente servant d’objectif au projecteur.

L’image est visible sur un écran placé à 5,0 m de la lentille.

Schéma :

1.  Sans souci d’échelle, construire graphiquement l’image A’B’ d’un objet AB à travers une lentille convergente.

2.  Calculer la valeur absolue du grandissement pour la situation étudiée.

3.  Calculer la taille de l’image A’B’ dans cette situation.

Le projecteur de diapositives :

1.  Construction graphique de  l’image A’B’ d’un objet AB à travers une lentille convergente.

-  Schéma :

-  Rayon 1 : issu du point B et passant par le centre optique : il n’est pas dévié.

-  Rayon 2 : issu du point B et parallèle à l’axe optique. Il émerge de la lentille en passant par le point F’ foyer - image.

-  Rayon 3 : issu du point B et passant par F (foyer - objet). Il émerge de la lentille parallèlement à l’axe optique.

2.  Valeur absolue du grandissement pour la situation étudiée.

-  La valeur absolue du grandissement  γ  permet de comparer la taille de l’image formée par une lentille à celle de l’objet.

-   

-  En utilisant le théorème de Thalès appliqué aux triangles OAB et OA’B’ :

-  On peut écrire la relation suivante :

-   

-  Les données :

-  Distance centre optique objet : OA = 8,0 cm

-  Distance centre optique image : OA’ = 5,0 m

-   

3.  Taille de l’image A’B’ dans cette situation.

-   

-  Dimensions de la diapositive 24 mm × 36 mm :

-  Environ : 1,5 m × 2,25 m ; 1,5 m × 2,3 m

Défaut de l’œil :

L’hypermétropie est un défaut de l’œil. L’hypermétrope voit net de loin, mais les objets proches lui paraissent flous, car les images se forment en arrière de la rétine.

Pour corriger l’hypermétropie, la personne peut porter des lentilles de contact.

L’ensemble {œil + lentille} se comporte alors comme une lentille mince convergente unique ayant une distance focale plus petite que celle de l’œil.

Les images se forment alors sur la rétine.

A.  Modèle de l’œil réduit hypermétrope non corrigé.

B.  Modèle de l’œil réduit hypermétrope corrigé.

1.  Reproduire le schéma A. puis trouver la position de l’image A’B’ de l’objet AB.

2.  Montrer que le schéma A. correspond bien à un œil hypermétrope.

3.  Reproduire le schéma B. et retrouver la position des foyers image F’ et objet F.

4.  Les résultats précédents sont-ils en accord avec la phrase écrite en italique ?

Défaut de l’œil :

1.  Reproduction du schéma A avec la position de l’image A’B’ de l’objet AB.

2.  Le schéma A. : un œil hypermétrope.

-  L’image A’B’ se fait en arrière de la rétine.

3.  Reproduction du schéma B. et position des foyers image F’ et objet F.

4.  Analyse des résultats :

-  On est bien en présence d’un œil hypermétrope.

-  L’image d’un objet proche se forme en arrière de la rétine.

Exercice à caractère expérimental :

On dispose d’une source lumineuse capable de projeter trois rayons lumineux parallèles entre eux.

1.  Proposer un protocole expérimental utilisant cette source lumineuse pour mesurer la distance d’une lentille mince convergente.

2.  Identifier les sources d’erreurs.

Exercice à caractère expérimental :

1.  Protocole expérimental utilisant cette source lumineuse pour mesurer la distance d’une lentille mince convergente.

-  On dispose d’une source lumineuse qui projette 3 rayons lumineux parallèles entre eux.

-  On utilise pour ce faire la propriété suivante : :

-  Tout rayon incident parallèle à l’axe principal d’une lentille convergente en émerge en passant par le point F’ appelé foyer - image de la lentille.

-  Le point F’ est situé après la lentille.

-  Ceci permet de connaître la position du point F’.

-  Pour connaître la distance focale, on mesure la distance OF’.

2.  Identifier les sources d’erreurs.

-  La lentille doit être perpendiculaire  aux rayons lumineux.

-  Les rayons lumineux doivent être proche de l’axe optique.

-  Le point délicat est de bien repérer le point d’intersection des 3 rayons lumineux.

-  ­Le plus souvent, on observe une tache lumineuse.

-  Il faut déplacer l’écran afin d’observer une tache lumineuse la plus petite possible.

-  Remarque :

-  Lorsque l’on veut connaître rapidement la distance focale d’une loupe, on dirige l’axe optique de la lentille vers le Soleil.

-  On place un écran afin d’obtenir une image quasi ponctuelle très lumineuse

(Attention, on peut mettre le feu à l'écran en papier si l'expérience dure trop longtemps).

Attention :

On peut mettre le feu à la feuille de papier

-  La tache lumineuse obtenue sur l’écran est l’image du Soleil donnée par la lentille convergente.

-  On peut considérer que le Soleil est une source lumineuse située à l’infini.

-  Les rayons provenant du Soleil sont parallèles à l’axe optique de la lentille.

-  L’image du Soleil se forme au foyer image F’ de la lentille convergente.

-  On en déduit ainsi la valeur approchée de la distance focale de la lentille convergente.

Côté Maths :

1.  Reproduire et compléter le schéma  ci-dessous avec une lentille mince convergente et les légendes suivante :

- Objet, image, centre optique

2.  Sachant que OB = 5,0 cm ; OC = 10,0 cm ;

AB = 3,0 cm, calculer la longueur CD.

Accommodation de l’œil :

Pour que les images soient situées sur la rétine, le cristallin change de forme : c’est l’accommodation.

Le schéma, les distances et les proportions ne correspondent pas à celles de l’œil réel.

Schéma :

1.  Reproduire et compléter le schéma pour trouver la position de l’objet AB donnant l’image A’B’ sur l’écran.

2.  Rapprocher l’objet AB de 3 ,0 cm de la lentille et trouver les nouvelles positions des foyers objet F et image F’ pour que l’image A’B’ se forme à nouveau sur l’écran.

3.  Quelle caractéristique de l’œil est modifiée lors de l’accommodation ?

Formation d’une image sur la rétine :

Le schéma suivant est celui de l’œil réduit.

Sur ce schéma, l’image A’B’ se forme sur l’écran.

-  Schéma :

1.  Recopier le schéma et compléter ses légendes.

2.  Déterminer la position de l’objet AB donnant l’image réelle A’B’ sur l’écran et la valeur absolue du grandissement.

3.  Accommodation :

a.  Refaire le schéma en éloignant l’objet de la lentille.

b.  Cette image se forme-t-elle sur l’écran ?

4.  Quelle caractéristique de l’œil doit-il modifier pour que l’image se forme systématiquement sur la rétine ?

DS : Les lentilles liquides :

A.   Principe de fonctionnement.

Les lentilles liquides sont constituées de deux fluides non miscibles (eau-huile) placés dans une capsule.

L’adhérence des fluides sur les parois de cette capsule varie lorsqu’une tension électrique est appliquée sur ces parois,

ce qui entraîne une déformation se la surface de contact eau / huile dont la courbure varie.

La lentille liquide se comporte alors comme une lentille mince convergente dont la distance focale change en fonction de la tension électrique appliquée.

L’image réelle de l’objet photographié se forme sur un capteur situé à une distance fixe de la lentille.

B.   Vue en coupe d’une capsule.

1.  Distance focale :

a.  Expliquer comment on fait varier la distance focale d’une lentille liquide.

b.  Comment nomme-t-on le point d’intersection des rayons lumineux ayant traversé la lentille liquide (schéma B.) ?

c.  Citer un point commun entre le fonctionnement d’une lentille liquide et celui de l’œil.

2.  On repère sur le capteur la position de l’image A’B’ d’un objet AB placé à 60 mm de la lentille.

La taille de l’image est 1,5 mm et celle de l’objet est 15 mm.

Par application du théorème de Thalès, calculer la distance OA’.

3.  Schéma :

a.  Faire un schéma de la lentille, de l’objet et de son image, puis repérer

la position du foyer image F’.

Choisir l’échelle suivante :

1 cm sur le schéma représente 3 mm dans

la réalité.

b.  Mesurer la distance focale.

4.  Caractéristiques de l’image :

a.  L’image se formant toujours sur le capteur, calculer sa nouvelle sa nouvelle taille lorsque l’objet se rapproche de 30 mm de la lentille.

b.  Pour que l’image se forme toujours sur le capteur, la distance focale est maintenant 5,0 mm.

Retrouver par construction graphique la taille de l’image calculée précédemment, en utilisant la même échelle.

DS : Les lentilles liquides  :

1.  Distance focale :

a.  Variation la distance focale d’une lentille liquide :

-  La lentille liquide se comporte alors comme une lentille mince convergente dont la distance focale change en fonction de la tension électrique appliquée.

-  L’adhérence des fluides sur les parois de cette capsule varie lorsqu’une tension électrique est appliquée sur ces parois,

ce qui entraîne une déformation se la surface de contact eau/huile dont la courbure varie

b.  Nom du point d’intersection des rayons lumineux ayant traversé la lentille liquide (schéma B.) :

-  Tout rayon incident parallèle à l’axe principal d’une lentille convergente en émerge en passant par le point F’ appelé foyer - image de la lentille.

-  Le point F’ est situé après la lentille.

-  Le point d’intersection des rayons lumineux ayant traversé la lentille liquide est le foyer – image de la lentille F’.

c.  Point commun entre le fonctionnement d’une lentille liquide et celui de l’œil.

-  Lorsque l’œil accommode, il modifie sa distance focale.

De même, les lentilles liquides modifient leur distance focale afin que l’image d’un objet se forme sur le capteur situé à une distance fixe.

2.  Valeur de la distance OA’.

-  On peut faire la représentation graphique de la situation :

-  On trace l’axe optique Δ.

-  On position l’objet AB et on trace le rayon lumineux qui passe par l’axe optique et qui n’est pas dévié.

-  Puis on position l’image A’B’

-  On obtient la figure suivante (sans soucis d’échelle) :

-  Les différentes mesures :

-  L’objet se trouve à 60 mm de la lentille : OA ≈ 60 mm

-  L’objet mesure environ 15 mm : AB ≈ 15 mm

-  La distance focale mesure (inconnue) : OF’ = f’ ≈ ?

-  L’image se trouve à (à déterminer) de la lentille : OA’ ≈ ?

-  L’image mesure 1,5 mm : A’B’ ≈ 1,5 mm

-  Par application du théorème de Thalès, aux triangles suivants :

- OAB et OA’B, on peut écrire la relation suivante :

-   

-  On en déduit la valeur de la distance OA’ :

-   

-  Schéma réalisé avec l’échelle de la question 3.:

3.  Schéma :

a.  Schéma de la lentille, de l’objet et de son image, puis repérer

la position du foyer image F’.

-  Échelle suivante :

1 cm sur le schéma représente 3 mm dans la réalité.

b.  Mesure de la distance focale.

-  Mesure sur le schéma : ℓ (f’) ≈ 1,8 cm

-  En conséquence :

-  f’ ≈ 3 × 1,8 mm

-  f’ ≈ 5,4 mm

4.  Caractéristiques de l’image :

a.  Valeur de sa nouvelle sa nouvelle taille lorsque l’objet se rapproche de 30 mm de la lentille.

-  Les différentes mesures :

-  L’objet se trouve à 30 mm de la lentille : OA ≈ 30 mm

-  L’objet mesure 15 mm : AB ≈ 15 mm

-  La distance focale mesure : OF’ = f’ = 5,0 mm

-  L’image se trouve à 6,0 mm de la lentille : OA’ ≈ 6,0 mm

-  L’image mesure ( à déterminer) : A’B’ ≈ ?

-  Schéma de la nouvelle situation :

-  Maintenant, on trace le rayon qui passe par le centre optique O et qui n’est pas dévié.

-  Taille de l’image :

-  Par application du théorème de Thalès, aux triangles suivants :

- OAB et OA’B, on peut écrire la relation suivante :

-   

-  On en déduit la valeur de la distance A’B’ :

-   

b.  Construction graphique, distance focale f’ et taille de l’image A’B’ :

-  L’objet se trouve à 30 mm de la lentille : OA ≈ 30 mm

-  L’objet mesure 15 mm : AB ≈ 15 mm

-  La distance focale mesure : OF’ = f’ = 5,0 mm

-  L’image se trouve à 6,0 mm de la lentille : OA’ ≈ 6,0 mm

-  L’image mesure ( à déterminer) : A’B’ ≈ 3,0 mm