|
|
Lumière : Ondes et particules Exercices |
|
|
|
|
1)- Exercice 03 page 348 : Connaître la longueur d’onde et la fréquence :
|
Connaître la longueur d’onde et la fréquence : 1. Rappeler la relation entre la fréquence ν d’une onde et la longueur d’onde λ. En déduire que 1 Hz = 1 s–1. 2. La longueur d’onde d’une onde électromagnétique de fréquence très élevée est-elle plus grande ou
plus petite que celle d’une onde de petite fréquence ? |
|
Connaître la longueur d’onde et la fréquence : 1.
Relation entre la fréquence ν d’une
onde et la longueur d’onde λ :
►
Relation fondamentale :
-
Remarque : pour les
radiations lumineuses, on préfère utiliser la lettre grecque ‘’nu’’.
-
Grandeur physique et unité : -
Terminologie :
- 2.
Longueur d’onde et la fréquence :
-
D’après la relation suivante :
-
-
La fréquence est inversement
proportionnelle à la longueur d’onde.
- Si la fréquence augmente
ν ↑ , alors
- Au plus la fréquence
ν
est grande et au
plus la longueur d’onde λ est
petite. Ou |
2)- Exercice 07 page 348 : Convertir des unités :
|
Convertir des unités : 1.
Convertir les longueurs d’onde des ondes
électromagnétiques suivantes en mètre :
-
500 nm ; 3,5 μm ; 15 pm ; 2,5 mm. 2.
Indiquer
l’(les) onde(s) appartenant au domaine du visible. |
|
Convertir des unités : 1. Longueurs
d’onde des ondes électromagnétiques en mètre :
-
500 nm ; 3,5 μm ; 15 pm ; 2,5 mm.
-
Multiples et sous multiples d’une
unité.
- Exemples : le kilomètre : km ; le kilowatt : kW ; - le millimètre :
mm.
-
500 nm = 500 × 10–9 m =
5,00 × 10–7 m
-
3,5 μm = 3,5 × 10–6 m
-
15 pm = 15 × 10–12 m = 1,5
× 10–11 m
-
2,5 mm = 2,5 × 10–3 m 2.
Domaine
du visible.
-
400 nm ≤
λ ≤ 780 nm
-
Radiation concernée :
λ = 500 nm
- Spectre du domaine visible :
|
3)- Exercice 08 page 348 : Donner un ordre de grandeur :
|
Donner un ordre de grandeur : 1.
Donner un ordre de grandeur, en hertz, des
fréquences suivantes :
-
Tableau :
2.
Attribuer chacune des fréquences à un
domaine d’application d’ondes électromagnétiques :
-
Scanner, téléphonie mobile,
fibroscopie, Wifi. |
Donner un ordre de grandeur : 1.
Ordre de grandeur, en hertz, des fréquences
suivantes :
-
Tableau : Fréquence
Ordre
de grandeur
en Hz
Domaine
d’application
107
THz
107
× 1012 = 1019
700
MHz
700 ×
106 ≈ 109
6 ×
1015 Hz
6 ×
1015 ≈ 1016
5 GHz
5 ×
109 ≈ 1010 2.
Domaine d’application d’ondes
électromagnétiques :
-
Scanner, téléphonie mobile,
fibroscopie, Wifi. Fréquence
Ordre
de grandeur
en Hz
Domaine
d’application
107
THz
107
× 1012 = 1019
Radiographie X
Scanner
700
MHz
700 ×
106 ≈ 109
Téléphonie mobile
6 ×
1015 Hz
6 ×
1015 ≈ 1016
Fibroscopie
5 GHz
5 ×
109 ≈ 1010
Wifi
![]()
4)- Exercice 09 page 349 : Calculer une énergie à partir d’une fréquence :
|
Une lampe à vapeur de sodium émet des radiations de fréquence
ν égale à 5,1 × 1014 Hz. 1.
Calculer l’énergie associée à cette
radiation, en joule et en électronvolt. 2.
Quelle particule transporte cette énergie ?
-
Données :
-
h = 6,63 × 10 – 34
J . s
-
1 eV = 1,60 × 10–19
J |
Calculer une énergie à partir d’une fréquence : Une lampe à vapeur de sodium émet des radiations de fréquence
ν égale à 5,1 × 1014 Hz.
-
Données :
-
h = 6,63 × 10 – 34
J . s
-
1 eV = 1,60 × 10–19
J 1.
Énergie associée à cette radiation, en joule
et en électronvolt.
-
Relation :
-
-
-
2.
Particule qui
transporte cette énergie :
-
Cette énergie est transportée par un
photon.
-
Additif :
-
Exemple spectre d’émission
et d’absorption de l’atome de sodium :
-
Profil spectral :
-
En réalité, il s’agit d’un
doublet : 589,0 nm et 589,6 nm :
-
On peut retrouver la valeur de la
longueur d’onde de l’onde de la radiation émise à partir de la
valeur de la fréquence :
-
-
Ce résultat est en accord avec le
spectre de l’atome de sodium.
![]()
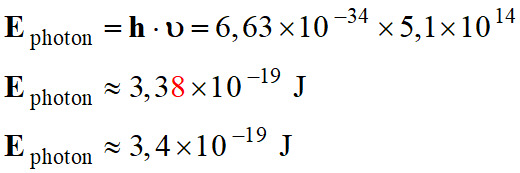
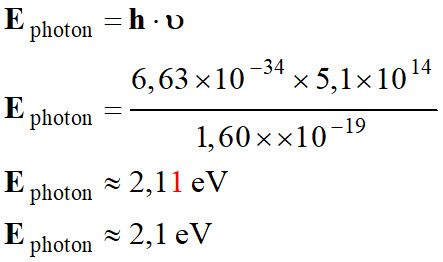
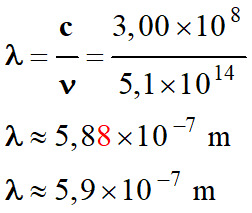
![]()
5)- Exercice 11 page 349 : Identifier une transition énergétique :
|
Identifier une transition énergétique : 1.
Sur le diagramme énergétique simplifié d’un
atome ci-dessous, quelle flèche représente une absorption ? 2.
Dans le cas où la fréquence associée
appartient au domaine du visible, à quoi correspond-elle dans un
spectre lumineux ?
|
|
Identifier une transition énergétique : 1.
Flèche qui représente une absorption :
-
Schéma :
- La flèche qui correspond à l'absorption d'un photon est la flèche verte (b). - Dans ce cas,
Einitial <
Efinal
-
L’atome gagne de l’énergie
en absorbant un photon.
-
Sur un diagramme d’énergie,
on représente cette transition par une
flèche
verticale
orienté vers le haut.
-
L’énergie absorbée est égale
à la différence d’énergie entre les deux niveaux :
-
ΔE
= | Efinal –
Einitial |
-
Cette énergie est
transportée par un photon :
-
Ephoton =
ΔE = |
Efinal –
Einitial | =
h .
ν
-
La fréquence
ν
découle de la différence d’énergie
ΔE
= | Efinal –
Einitial | - L’absorption d’énergie lumineuse par un atome ne peut se faire que si l’énergie du photon permet
une transition d’un niveau
Einitial à un niveau supérieur
Efinal tel que :
-
Efinal –
Einitial =
h
. ν 2.
Absorption d’un photon dans le spectre
visible :
-
Si cette fréquence
ν
appartient au domaine du visible, elle correspond alors à une raie
noire dans le spectre de la lumière blanche.
-
Exemple :
|
6)- Exercice 13 page 349 : Calculer une énergie à partir d’un spectre :
|
Calculer une énergie à partir d’un spectre : Le spectre d’absorption d’une entité chimique comporte trois
raies de longueurs d’onde 450 nm, 530 nm et 750 nm.
-
Calculer en joule et en électron
volt, l’énergie de la transition correspondante dans le rouge.
-
Données :
-
h = 6,63 × 10 – 34
J . s
-
1 eV = 1,60 × 10–19 J |
|
Calculer une énergie à partir d’un spectre :
-
Énergie de la transition
correspondante à la radiation rouge.
-
Valeur de la longueur d’onde :
-
λR = 730 nm
-
Relation :
-
-
-
-
Tableau récapitulatif :
|
7)- Exercice 14 page 349 : Déterminer la couleur d’une raie :
|
Déterminer la couleur d’une raie : Une transition entre deux états provoque l’émission d’un photon
d’énergie E = 2,76 eV. À l’aide du spectre ci-dessous, déterminer la couleur de la raie
observée.
-
Données :
-
h = 6,63 × 10 – 34
J . s
-
1 eV = 1,60 × 10–19
J |
|
Déterminer la couleur d’une raie :
-
Données :
-
h = 6,63 × 10 – 34
J . s
-
1 eV = 1,60 × 10–19
J
-
Énergie du photon :
E = 2,76 eV
-
Couleur de la raie observée :
-
Il s’agit de l’émission d’un photon.
-
Dans ce cas,
Einitial >
Efinal
-
L’atome perd de l’énergie en
émettant un photon. - Sur un diagramme d’énergie, on représente cette transition par une
flèche
verticale
orienté vers le bas.
-
L’énergie libérée est égale
à la différence d’énergie entre les deux niveaux :
-
ΔE
= | Efinal –
Einitial |
-
Cette énergie est
transportée par un photon :
-
Ephoton =
ΔE = |
Efinal –
Einitial | =
h .
ν
-
La fréquence
ν
découle de la différence d’énergie
ΔE
= | Efinal –
Einitial |
-
Dans le cas présent :
-
Ephoton =
ΔE
= E = 2,76 eV
-
Valeur de la longueur d’onde de la
radiation émise :
-
Attention : la
valeur de l’énergie est exprimée en électronvolt (eV)
-
-
Il s’agit d’une radiation de couleur
bleue :
|
8)- Exercice 15 page 349 : Exploiter une transition énergétique :
|
Exploiter une transition énergétique : 1.
Transition énergétique : a.
Quelle énergie doit posséder un photon pour
permettre à l’atome de passer du niveau d’énergie E1
au niveau d’énergie E∞ ? b.
Représenter cette transition. 2.
Calculer la longueur d’onde correspondante.
-
1 eV = 1,60 × 10–19 J |
Exploiter une transition énergétique : 1.
Transition énergétique : a.
Énergie du photon pour permettre à l’atome
de passer du niveau d’énergie E1 au niveau
d’énergie E∞ :
-
Il s’agit d’une absorption.
-
L’énergie absorbée est égale
à la différence d’énergie entre les deux niveaux :
-
Ephoton =
ΔE = |
Efinal –
Einitial | = |
E∞ –
E1 |
-
Ephoton = | 0 – (– 13,6) |
-
Ephoton = 13,6 eV b.
Représenter cette transition.
-
Dans ce cas,
Einitial <
Efinal
-
L’atome gagne de l’énergie
en absorbant un photon.
-
Sur un diagramme d’énergie,
on représente cette transition par une
flèche
verticale
orienté vers le haut.
-
Schéma de la transition : 2.
Calculer la longueur d’onde correspondante.
-
Cette énergie est
transportée par un photon :
-
Ephoton =
ΔE = |
E∞ –
E1 | =
h
. ν
-
La fréquence
ν
découle de la différence d’énergie
ΔE
= | E∞ –
E1 |
-
L’absorption d’énergie
lumineuse par un atome ne peut se faire que si l’énergie du photon
permet une transition d’un niveau
Einitial à un niveau supérieur
Efinal tel que :
-
Ephoton =
|
Efinal –
Einitial |
= |
E∞ – E1 | = h . ν
-
Ephoton ≈ 13,6
eV
-
Valeur de la longueur d’onde
λ de la radiation émise :
-
Attention :
la valeur de l’énergie est
exprimée en électronvolt (eV)
-
-
La radiation appartient au domaine
des U.V.
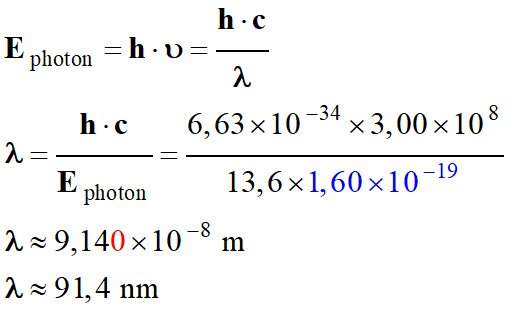
![]()
9)- Exercice 16 page 349 : Utiliser un diagramme d’énergie :
|
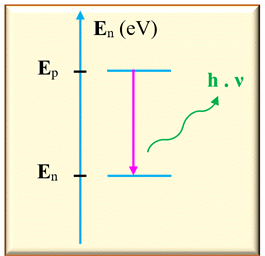
Utiliser un diagramme d’énergie : Le schéma ci-dessous représente une transition entre deux états
d’énergie d’un atome. 1.
Cette transition s’accompagne-t-elle d’une
absorption ou d’une émission de photon ? 2.
Que représentent Ep et
En ? Que représente h × ν ? 3.
Quelle relation existe-t-il entre h ×
ν , Ep et En ?
|
Utiliser un diagramme d’énergie : 1.
Type de transition :
-
La transition est
représentée par une
flèche verticale orienté vers le
bas.
-
L’atome perd de l’énergie en
émettant un photon.
-
Il s’agit de l’émission d’un photon 2.
Signification de Ep et
En. Signification de h × ν :
-
Ep et
En
représentent deux des niveaux
d’énergie de l’atome.
-
L’atome ne peut exister que
dans certains états d’énergie ou niveaux d’énergie bien définis.
-
Les énergies d’un atome sont
quantifiées.
-
Au cours d’une transition entre les
deux états d’énergie Ep et En,
avec Ep > En, le photon émis par
l’atome possède une énergie telle que :
-
Ephoton =
h ×
ν 3.
Relation entre h × ν , Ep
et En :
-
Ep - En
= h . ν
-
L’énergie libérée est égale
à la différence d’énergie entre les deux niveaux.
-
La fréquence
ν
découle de la différence d’énergie :
ΔE = Ep - En
![]()
10)- Exercice 20 page 350 : Thermographie :
|
Thermographie : La thermographie est devenue un outil très efficace pour les diagnostics énergétiques des bâtiments. Cette technique repose sur l’émission, par tout corps, d’un
rayonnement électromagnétique dépendant de la température de surface.
1. Une radiation de fréquence ν = 32,2 THz est détectée par un appareil de thermographie. Déterminer sa longueur d’onde. 2.
Cette radiation est-elle située dans le
domaine du visible, de l’infrarouge ou de l’ultraviolet ? 3. Dans ce domaine, les radiations sont souvent caractérisées par leur nombre d’onde σ. À l’aide de la formule Ephoton
= h . c . σ, indiquer l’unité de σ. |
|
Thermographie :
1.
Longueur d’onde de la radiation de fréquence
ν = 32,2 THz
-
2.
Domaine de la radiation :
-
La radiation de longueur d’onde
λ ≈ 9,32 × 10–6
m appartient au domaine de l’infrarouge (IR). 3.
Unité de σ.
-
Formule :
-
Ephoton = h
. c . σ
-
Autre formulation :
-
-
On en déduit la relation
suivante entre le nombre d’onde et la longueur d’onde :
-
-
Le nombre d’onde
σ est l’inverse de la longueur d’onde
λ.
-
L’unité de longueur d’onde est le
mètre : m
-
L’unité du nombre d’onde est m–1.
-
Additif :
-
Spectres IR.
-
La spectroscopie
IR est une spectroscopie d’absorption.
-
Les composés organiques absorbent
aussi dans le domaine de l’infrarouge.
-
Pour ces spectres, on fait figurer :
-
La transmittance
T ou intensité lumineuse transmise par l’échantillon analysé en
ordonnée (elle s’exprime en pourcentage)
-
Le nombre d’ondes
σ en abscisse.
-
Le nombre d’ondes
σ est l’inverse de la longueur d’onde
λ.
-
Généralement, le nombre d’ondes σ
s’exprime en cm–1 en chimie organique.
-
En chimie organique, les radiations
infrarouges exploitées vont
de 400 cm–1 à 4000 cm–1. (25 μm à 250 μm)
-
Cette spectroscopie peut se faire en
phase gazeuse ou en phase condensée.
-
Exemple : Spectre de la propanone. |
11)- Exercice 26 page 352 : Lumière d’une étoile : Véga :
|
Lumière d’une étoile : Véga : Véga est l’étoile la plus brillante de la constellation de la
Lyre. Elle est située à 25 années-lumière du système solaire. - Le spectre de la lumière venant de Véga montre-t-il, aux erreurs de mesures près la présence
d’hydrogène autour de cette étoile ? A.
Spectre de la lumière de Véga.
B.
Diagramme de quelques niveaux d’énergie de
l’atome d’hydrogène.
C.
La lumière d’une étoile. Les étoiles se comportent comme des corps chauds : Elles émettent de la lumière dont le spectre est continu. Après émission, cette lumière traverse les couches de gaz qui
entourent l’étoile. L’interaction entre la lumière et les entités contenues dans ces
gaz provoque une absorption de certaines radiations.
-
Données :
-
h = 6,63 × 10 – 34
J . s
-
1 eV = 1,60 × 10–19 J |
|
Lumière d’une étoile : Véga : - Les raies noires présentes dans le spectre de la lumière provenant de l’étoile Véga permettent d’identifier
les espèces chimiques présentes dans l’atmosphère qui
entoure cette étoile.
-
L’atmosphère de Véga contient des
éléments chimiques.
-
La partie haute de l’atmosphère
absorbe une partie de la lumière émise dans la partie basse.
-
Il en résulte des raies d’absorption
dans le spectre continu.
-
Ce sont les raies d’absorption des
éléments chimiques présents dans l’atmosphère de Véga.
-
Si Véga ne comportait pas
d’atmosphère, le spectre de la lumière émise serait continu.
-
L’existence des raies d’absorption
est dû à la présence d’une atmosphère autour Véga.
-
Un spectre d’émission ou d’absorption
est caractéristique d’une entité chimique..
-
Un spectre de raies d’émission ou d’absorption permet
d’identifier une entité chimique.
-
C’est sa carte d’identité, sa
signature.
-
Longueurs d’onde des différentes
radiations présentes dans le spectre d’absorption de l’étoile Véga.
-
Tableau de valeurs : référence : 400
nm
-
Correspondance avec le diagramme
d’énergie de l’atome d’hydrogène.
-
Comme, les radiations appartiennent
au domaine du visible, on ne va pas faite intervenir les niveaux
d’énergie E1
et E∞.
-
Relation permettant de calculer la
valeur de la longueur d’onde en nm :
-
-
Pour avoir la valeur de la longueur
d’onde de la radiation, on multiple la valeur trouvée par 109.
-
On part du niveau initial :
E6
-
On envisage toutes les transitions
possibles jusqu’au niveau d’énergie
E2.
-
Comme les énergies sont exprimées en
eV, il faut utiliser la relation :
-
1 eV = 1,60 × 10–19 J
-
Ainsi pour la transition du niveau
initial E6, au
niveau final E2 :
-
Ephoton =
E6 –
E2
-
-
On réalise un tableau avec le tableur
Excel :
-
Formule dans la cellule G7 (que l’on
recopie vers le bas autant que nécessaire)
-
Le spectre de la lumière venant de
Véga montre, aux erreurs de mesures près, la présence d’hydrogène
autour de cette étoile.
-
Car un atome absorbe les radiations
qu’il est capable d’émettre.
-
La radiation
λ5 provient d’une autre entité chimique présente dans
l’atmosphère qui entoure l’étoile Véga.
-
La série de Balmer : - La série de Balmer est la série de raies spectrales de l'atome d'hydrogène correspondant à une transition énergétique
d’un niveau d’énergie
En, avec
n
> 2 vers le niveau d’énergie
En, avec n
= 2.
-
Tableau :
- La radiation λ72 fait intervenir le niveau d’énergie E7 qui n’est pas donné dans le diagramme d’énergie de l’atome d’hydrogène
(on
s’est arrêté au niveau d’énergie
E6) |
|
|