|
|
L'énergie des systèmes électriques Exercices |
|
|
|
|
1)- Exercice 05 page 248 : Exploiter l’équation d’une caractéristique :
|
Exploiter l’équation d’une caractéristique : L’équation de la caractéristique d’une pile est : U = 4,5 – 2 I, Avec U en volt et I en ampère.
-
Identifier la force électromotrice
E et la résistance
r de cette pile. |
|
Exploiter l’équation d’une caractéristique :
-
Équation de la caractéristique d’une
pile :
-
U = 4,5 – 2 I,
-
C’est une source réelle de tension. - Une source réelle de tension peut être modélisée par l’association série - d’une source idéale de tension de f.é.m E - et
d’un conducteur ohmique de résistance
r.
-
U =
E –
r
. I
-
La f.é.m
E représente la tension à
vide de la pile (I = 0 A)
-
Dans le cas présent :
-
E = 4,5 V
-
La résistance interne de la pile :
-
r = 2 Ω. |
2)- Exercice 07 page 248 : Exploiter une caractéristique :
|
Exploiter une caractéristique : La caractéristique d’une source réelle de tension continue est la
suivante :
-
Caractéristique U = f (I)
: 1.
Écrire l’équation littérale de la
caractéristique U = f (I). 2.
Déterminer la valeur de la force
électromotrice E et la valeur de la résistance interne r à
l’aide de la caractéristique.
|
|
Exploiter une caractéristique :
-
Caractéristique U = f (I)
: 1.
Équation littérale de la caractéristique
U = f (I).
-
On est en présence d’une source
réelle de tension continue. - Une source réelle de tension peut être modélisée par l’association série - d’une source idéale de tension de f.é.m E - et d’un conducteur ohmique de résistance r.
-
La valeur de la tension
UPN aux bornes de la source réelle de courant dépend de la valeur de l’intensité
I débitée.
-
La valeur de la tension
UPN aux bornes de la source réelle de courant diminue lorsque la
valeur de l’intensité I
débitée augmente. UPN
= E – r . I ou U = E – r . I
-
Valeur de la force électromotrice
E :
-
C’est la tension à vide de la source
réelle de tension (I = 0)
-
C’est l’ordonnée à l’origine
b de la droite du type : U
= a I + b
-
Dans le cas présent :
-
E = 4,5 V
-
Valeur de la résistance interne
r :
-
La résistance interne r de la
source réelle de tension est égale à l’opposé
du coefficient directeur de la droite représentant la
caractéristique U =
f (I) :
-
r = –
a.
-
Valeur du coefficient directeur
a :
-
Exploitation de la représentation
graphique : - Une méthode : on choisit deux points A et B de la droite représentant la caractéristique U = f (I).
-
-
Or :
r = –
a.
-
r ≈ 1,0 Ω |
3)- Exercice 10 page 249 : Calculer une énergie électrique :
|
Calculer une énergie électrique : Sur un adaptateur secteur, on peut lire les informations
suivantes :
1.
Relever la tension de sorite et l’intensité
du courant de sortie. 2.
Calculer la puissance électrique en sortie
de cet l’adaptateur. 3.
Calculer l’énergie électrique fournie par
l’adaptateur durant 60 secondes de fonctionnement. |
Calculer une énergie électrique : Informations : 1.
Tension de sorite et intensité du courant de
sortie.
-
Valeur de la tension de sortie US
:
-
US = 9 V
-
Valeur de l’intensité du courant de
sortie IS :
-
IS
= 1 A 2.
Puissance électrique en sortie PS
de cet l’adaptateur :
-
PS =
US .
IS.
-
PS ≈ 9 ×
1
-
PS ≈ 9 W 3.
Énergie électrique fournie par
l’adaptateur durant 60 secondes de fonctionnement.
-
W =
PS .
Δt
-
W ≈ 9 ×
60
-
W ≈ 5,4
×102 J
-
W ≈ 5 ×102 J

![]()
![]()
4)- Exercice 11 page 248 : Calculer une durée de fonctionnement :
|
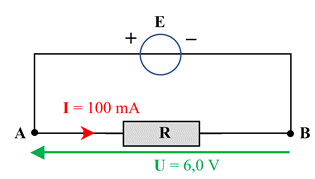
Calculer une durée de fonctionnement : Un conducteur ohmique, placé dans un circuit électrique, est traversé par un courant électrique d’intensité constante I = 100 mA durant 30 minutes. La tension à ses bornes est 6,0 V. 1.
À partir de l’expression P = U
. I, exprimer l’énergie électrique reçue en fonction de Δt,
U et I. 2.
Calculer la valeur de l’énergie électrique
reçue. |
Calculer une durée de fonctionnement : 1.
Expression de
l’énergie électrique reçue en fonction de Δt, U
et I.
-
Puissance électrique reçue :
-
P =
U .
I
-
Énergie électrique reçue :
-
W =
P . Δt
-
W =
U .
I . Δt 2.
Valeur de l’énergie électrique reçue.
-
W =
U .
I . Δt
-
W = 6,0 × 100 × 10–3
× 30 × 60
-
W ≈ 1,08
× 103 J
-
W ≈ 1,1 × 103
J
![]()
5)- Exercice 12 page 249 : Exprimer un rendement :
|
Exprimer un rendement : On représente ci-dessous la chaîne de puissance d’une batterie de
téléphone en charge. 1.
Définir le rendement. 2.
Expliquer pourquoi le rendement ne peut pas
être supérieur à 1. |
|
Exprimer un rendement : 1.
Définir le rendement.
-
Chaîne de puissance d’un
convertisseur :
-
Le rendement η de conversion
d’un convertisseur est une grandeur sans dimension qui mesure
l’efficacité de la conversion :
-
Dans le cas de la batterie en
charge : Chaîne de puissance :
-
Le rendement η de conversion
d’un convertisseur est une grandeur sans dimension qui mesure
l’efficacité de la conversion :
-
Remarque : le rendement η est
toujours inférieur ou égal à 1. 2.
Le rendement ne peut pas être supérieur à 1. - La batterie est une source réelle de tension. - Elle possède une résistance interne r.
-
Lors de son fonctionnement, il y des
pertes par effet Joule.
-
En conséquence, la puissance
exploitable est toujours inférieure à la puissance d’entrée.
-
Dans le cas présent, la puissance
chimique est toujours inférieure à la puissance électrique (lors de
la charge).
-
Le rendement η est inférieur à
1.
-
Remarque : lors de la décharge de la
batterie du téléphone, c’est l’inverse qui se produit.
|
6)- Exercice 13 page 249 : Calculer un rendement :
|
Calculer un rendement : Un moteur électrique, d’un jouet pour enfant, est soumis à une
tension de U = 4,5 V. Il est traversé par un courant d’intensité I = 0,050 A. Il fournit une puissance mécanique Pmec = 0,20 W et transfère par effet Joule, au milieu extérieur, une puissance Pth .
1.
Calculer la puissance électrique en entrée. 2.
Calculer le rendement
ηM du moteur
électrique. |
|
Calculer un rendement :
1.
Puissance électrique en entrée.
-
Pentrée =
U .
I
-
Pentrée = 4,5
× 0,050
-
Pentrée ≈
0,225 W
-
Pentrée ≈
0,23 W 2.
Rendement
ηM du moteur
électrique.
-
Bilan de puissance du convertisseur :
-
Dans le cas du moteur électrique :
-
Rendement ηM du
moteur électrique :
-
- Remarque : - Au cours de la conversion,
la puissance se conserve :
-
Pentrée =
Pmec + Pth
-
Pth = Pentrée
– Pmec ≈ 0,23
–0,20 - Pth ≈ 2,5 × 10–2 W |
7)- Exercice 15 page 249 : La lampe de poche :
|
La lampe de poche : On a tracé sur le même graphique les caractéristiques U =
f (I) d’une lampe de poche et celle d’une pile. 1.
Indiquer, sur le schéma du montage
permettant d’obtenir la caractéristique de la pile,
le sens de branchement des multimètres. 2.
Déterminer la valeur de la force
électromotrice E et la valeur de la résistance interne r
de la pile. 3.
La lampe est reliée à la pile plate, Ulampe
= Upile. Déterminer la valeur de
l’intensité du courant I dans le circuit ? 4.
Calculer la puissance électrique reçue par
la lampe. 5.
Représenter la chaîne de puissance de la
lampe.
|
|
La lampe de poche : 1.
Sens de branchement des multimètres.
-
Schéma :
2.
Valeur de la force électromotrice E
et valeur de la résistance interne r de la pile.
-
On réalise l’exploitation graphique
de la caractéristique U = f (I) de la pile.
-
Valeur de la force électromotrice
E :
-
C’est la tension à vide de la source
réelle de tension (I = 0)
-
C’est l’ordonnée à l’origine
b
de la droite du type : U = a I + b
-
Dans le cas présent :
-
E ≈ 4,44 V
-
Valeur de la résistance interne
r : - La résistance interne r de la source réelle de tension est égale à
l’opposé
du coefficient directeur de
la droite représentant la caractéristique U = f (I):
-
r = – a.
-
Valeur du coefficient directeur a :
-
Exploitation de la représentation
graphique :
-
Une méthode : on choisit deux points
A et B de la droite représentant la caractéristique
U = f (I).
-
Coordonnées du point
A : (0,00 A ; 4,44 V)
-
Coordonnées du point
B :
-
Valeur de
UB :
-
Coordonnées du point
B : (IB = 300
mA : UB ≈ 4,22
V)
-
Valeur du coefficient directeur
a :
-
-
Or : r = – a.
-
r ≈ 0,73 Ω 3.
Valeur de l’intensité du courant I
dans le circuit ? - Le point d’intersection de de la caractéristique de la pile et de la lampe donne le point de
fonctionnement de l’association série de la pile et de la lampe :
-
Schéma du circuit :
-
U =
UPN =
UAB
-
Exploitation graphique :
-
Coordonnées du point d’intersection
C : (IC ≈ 275 mA : UC
= U ≈ 4,24 V)
-
L’intensité dans le circuit est
voisine de I ≈ 275 mA. 4.
Puissance électrique reçue PE
par la lampe.
-
PE =
U .
I = UC .
IC
-
PE ≈ 4,24 ×
275 ×10–3
-
PE ≈ 1,1667
W
-
PE ≈ 1,17 W
-
Ou :
PE ≈ 1,2 W 5.
Chaîne de puissance de la lampe.
-
Bilan de puissance :
-
Additif :
-
Rendement :
|
8)- Exercice 17 page 250 : Nucléaire et éolien :
|
Nucléaire et éolien :
Le parc nucléaire français a produit 379,1 TW.h en 2017, pour une
capacité de production de 63 GW. 1.
Identifier la puissance électrique
nucléaire, ainsi que l’énergie électrique produite en 2017. 2.
Calculer la durée moyenne de fonctionnement
des centrales nucléaires françaises en 2017. 3. Évaluer le nombre d’éoliennes qu’il faudrait installer pour remplacer le parc nucléaire français ? La puissance moyenne d’une
éolienne est de 3,0 MW.
-
Données :
-
1 TW.h = 1012 W . h.
-
1 MW.h = 106 W . h. |
Nucléaire et éolien : Le parc nucléaire français a produit 379,1 TW.h en 2017, pour une capacité de production de 63 GW. 1.
Puissance électrique nucléaire et l’énergie
électrique produite en 2017.
-
Puissance électrique nucléaire en
2017 :
-
PE = 63 GW =
63 × 109
-
PE = 6,3 × 1010
W
-
Énergie
électrique produite en 2017 :
-
WE = 379,1
TW.h = 379,1 × 1012 × 3600
-
WE ≈1,36476
× 1018 J
-
WE ≈1,365 × 1018
J
-
WE ≈1,365
EJ (exajoule) 2.
Durée moyenne de fonctionnement des
centrales nucléaires françaises en 2017.
-
Relation :
WE = PE
. Δt
-
On tire de cette relation :
-
-
Δt ≈ 2,5 ×102
j
-
Δt ≈ 0,69
an
3.
Nombre d’éoliennes N qu’il faudrait
installer pour remplacer le parc nucléaire français
-
La puissance moyenne d’une éolienne :
-
Péolienne =
3,0 MW = 3,0 ×106
W
-
Puissance électrique nucléaire en
2017 :
-
PE = 63 GW =
63 × 109
-
PE = 6,3 × 1010
W
-
Nombres d’éolienne :
-
-
Il faut installer environ 2,1 × 104
éoliennes pour remplacer le parc nucléaire français.


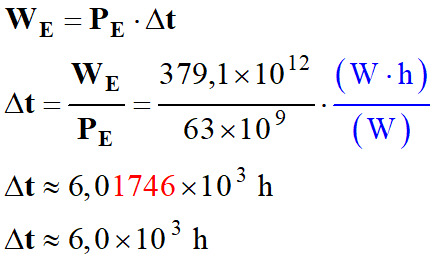
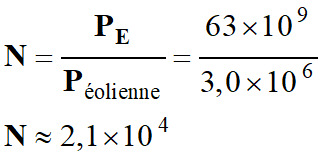
![]()
9)-Exercice 19 page 250 : Rendement d’une pile :
|
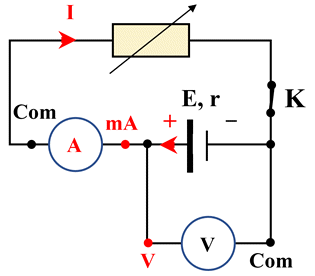
Rendement d’une pile : Pour tracer la caractéristique U = f (I) d’une pile, on utilise un conducteur ohmique de résistance réglable dans un montage schématisé ci-dessous :
1.
Reproduire le schéma en plaçant les deux
multimètres nécessaires à l’expérience. 2.
L’étude
a conduit au
tableau de mesures suivant :
a.
Tracer la caractéristique U = f
(I) de cette pile. b. Déterminer, à partir de la caractéristique, la résistance r et la force électromotrice E
de cette pile. 3.
Représenter la chaîne de puissance de la
pile. 4.
Calculer le rendement de la pile lorsqu’elle
est traversée par un courant I = 40 mA. |
Rendement d’une pile : 1.
Schéma du montage : 2.
Exploitation du
tableau de mesures : a.
Caractéristique U = f (I)
de cette pile.
-
Caractéristique 1 :
-
Les points sont sensiblement alignés.
-
La caractéristique est un segment de
droite qui ne passe pas par l’origine et la pente de cette droite
est négative.
-
La tension diminue lorsque
l’intensité augmente
-
À l'aide du tableur
Excel, on peut faire une étude statistique :
-
On trace une courbe de tendance, on
choisit le modèle ''linéaire''
-
et on demande l'équation de cette
droite et le coefficient de détermination.
-
Équation du type : Type mathématique
:
-
y =
a .
x + b
-
Traduction en physique :
-
U = a . I
+ b
-
U =
E –
r . I
-
Le coefficient de corrélation
R2
= 1.
-
L’adéquation entre les grandeurs est
parfaite.
-
Le modèle choisi est le mieux adapté. b.
Valeur de la résistance r et de la
force électromotrice E de cette pile.
-
Exploitation graphique :
-
La force électromotrice
E : c’est la tension à vide de la pile (I = 0 A)
-
C’est la valeur de l’ordonnée à
l’origine de la caractéristique
U =
f (I)
de cette pile.
-
Dans le cas présent :
-
E =
b ≈ 9,0 V
-
La résistance interne
r de la pile :
-
Elle est égale à l’opposée du
coefficient directeur de la caractéristique
U =
f (I)
de cette pile.
-
r = –
a -
-
r = –
a ≈ 3,3 Ω
-
U =
E –
r . I
-
U = 9,0 – 3,3 ×
I 3.
Chaîne de puissance de la pile.
-
Bilan de puissance :
-
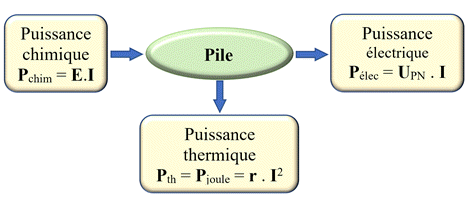
La pile électrique :
-
La pile électrique transforme de
l’énergie chimique en énergie électrique et en chaleur.
-
La pile électrique transforme une
puissance chimique en puissance électrique et en puissance
thermique.
-
La pile électrique est une source
réelle de tension : 4.
Rendement de la pile lorsqu’elle est
traversée par un courant I = 40 mA.
-
Son rendement
η est inférieur à 1.
-
-
Tension
U aux bornes de la pile :
-
U = 9,0 – 3,3 ×
I
-
U = 9,0 – 3,3 × 40 × 10–3
-
U ≈ 8,868
V
-
U ≈ 8,9
V
-
Valeur du rendement pour cette
intensité :
-
-
Une partie de la puissance chimique
stockée dans la pile est dégradée par effet joule à cause de la
résistance interne r de
la pile.
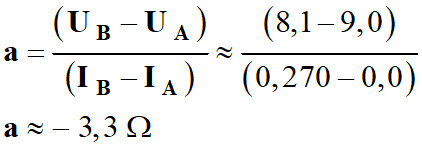

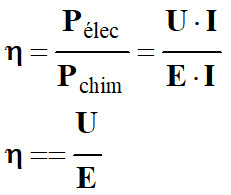
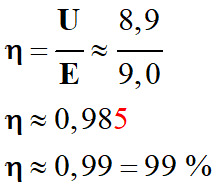
![]()
10)- Exercice 20 page 251 : Batterie d’un téléphone portable :
|
Batterie d’un téléphone
portable : L’image ci-dessous est celle d’une batterie de téléphone
portable.
1.
Quelle est la tension d’alimentation du
téléphone portable ? 2.
Que signifie l’indication « 1900 mAh » ? 3.
Autonomie et puissance : a.
Déterminer l’intensité moyenne du courant
débité par cette batterie dans le cas d’une autonomie de 8 h. b.
Calculer alors la puissance électrique
disponible aux bornes de la batterie. |
|
Batterie d’un téléphone portable :
1.
Tension d’alimentation du téléphone
portable :
-
La tension d’alimentation : U = 3,7 V
-
Indication :
DC : Direct Courant : courant continu. 2.
Indication « 1900 mAh » :
-
Ceci représente la charge électrique
de la batterie du téléphone portable :
-
Q = 1900 mA . h = 1900 ×
10–3 × 3600
-
Q = 6,84 × 103
C 3.
Autonomie et puissance : a.
Intensité moyenne du courant débité par
cette batterie dans le cas d’une autonomie de 8 h.
-
b.
Puissance électrique disponible aux bornes
de la batterie.
-
Pélec =
U .
I
-
Pélec ≈ 3,7 ×
2,4 × 102 × 10–3
-
Pélec ≈ 0,878
W
-
Pélec ≈ 0,88 W |
11)- Exercice 22 page 251 : Rendement d’une voiture :
|
Rendement d’une voiture Le marché de l’automobile électrique est en pleine expansion. Le moteur électrique d’un véhicule est alimenté par des batteries délivrant une énergie électrique de 41 kW . h. Le rendement du moteur électrique est proche de 80 %. 1.
Schématiser la chaîne de puissance du moteur
de l’automobile. 2.
Rendement, puissance et énergie : a.
Exprimer le rendement η en fonction
des puissances d’entrée et exploitable. b.
En utilisant la relation entre puissance et
énergie, établir l’expression du rendement η en
fonction des énergies. 3.
Calculer l’énergie exploitable fournie par
le moteur. |
|
Rendement d’une voiture 1.
Schéma de la chaîne de puissance du moteur
de l’automobile.
-
Cas général d’un convertisseur :
-
Rendement du convertisseur :
-
Cas d’un moteur électrique : 2.
Rendement, puissance et énergie : a.
Expression du rendement η en fonction
des puissances d’entrée et exploitable.
-
Le rendement
η de conversion d’un convertisseur est une grandeur sans dimension
qui mesure l’efficacité de la conversion :
-
Remarque : le rendement
η est toujours inférieur
ou égal à 1. b.
Expression du rendement η en fonction
des énergies.
-
En utilisant la relation entre
puissance et énergie, on obtient l’expression du rendement
η en fonction des énergies :
-
Wentrée = Pentrée
. Δt
-
Wexploitable = Pexploitable
. Δt
-
On tire :
3.
Énergie exploitable fournie par le moteur.
-
Wexploitable =
η .
Wentrée
-
Wexploitable =
0,80 × 41 kW . h
-
Wexploitable ≈
32,8 kW . h
-
Wexploitable ≈
33 kW . h
-
Wexploitable =
0,80 × 41 kW .
h
-
Wexploitable =
0,80 × 41 ×103 ×3600
-
Wexploitable ≈
1,1808 ×108 J
-
Wexploitable ≈ 1,2
×108 J |
12)- Exercice 24 page 251 : Vélo à assistance électrique :
|
Vélo à assistance électrique : Un vélo à assistance électrique est composé d’une batterie LI-ion qui alimente un moteur électrique. La notice fait apparaître les informations suivantes :
1.
Quelle est l’intensité du courant électrique
fourni par la batterie lorsque l’assistance
électrique est en fonction ? 2.
Déterminer la puissance mécanique disponible
à la sortie du moteur. 3.
En déduire la puissance perdue par le
moteur. 4.
Que signifie « capacité 10 A . h » ? 5.
Quelle est la durée d’utilisation de
l’assistance électrique ?
-
Données :
-
1 A . h = 1 A × 1 h |
|
Vélo à assistance électrique :
1. Intensité du courant électrique I fourni par la batterie lorsque l’assistance électrique est en
fonction :
-
Données :
-
La tension aux bornes de la
batterie :
-
U = 36 V
-
Puissance utile fournie par la
batterie :
-
Putile = 500 W
-
Intensité du courant électrique I
fourni par la batterie :
-
2.
Puissance mécanique Pmeca
disponible à la sortie du moteur.
-
Bilan de puissance du convertisseur :
avec la terminologie utilisée dans l’exercice.
-
Rendement du convertisseur :
-
Puissance mécanique
Pmeca disponible à la sortie du moteur :
-
Pmeca =
η .
Putile
-
Pmeca = 0,78 ×
500
-
Pmeca ≈ 3,9
×102 W 3.
Puissance perdue Pperdue
par le moteur.
-
Au cours d’une conversion, l’énergie
et la puissance sont des grandeurs qui se conservent :
-
Putile =
Pmeca + Pperdue
-
Pperdue = Putile
– Pmeca
-
Pperdue = 500 – 3,9 ×102
-
Pperdue = 1,1×102 W 4.
Signification de
« capacité 10 A . h » - La capacité représente la charge électrique portée par la batterie qui alimente le moteur électrique.
- On peut l’exprimer en coulomb (C) :
-
Q = 10 × 3600
-
Q = 3,6 ×104 C 5.
Durée d’utilisation Δt de
l’assistance électrique :
-
Relations :
-
-
Δt ≈ 0,72 × 60
-
Δt ≈ 43 min |
|
|