|
|
Description d'un fluide au repos Exercices |
|
|
|
|
1)- Exercice 04 page 204 : Connaître la masse volumique :
|
Connaître la masse volumique : Donner la formule permettant de calculer la masse volumique d’un fluide à partir de son volume et de sa masse. Indiquer les unités des grandeurs utilisées. |
|
Connaître la masse volumique : Formule permettant de calculer la masse volumique
ρ
d’un fluide à
partir de son volume V ,et de sa masse m.
-
Remarque : on exprime aussi les
masses volumiques en g . cm–3 ou g . mL–1.
-
Rappel : 1 m3 = 103
dm3 = 106 cm3 = 103 L
-
La masse volumique d’une espèce
chimique dépend de la température.
-
La masse volumique d’un gaz dépend de
la température et de la pression.
- Elles sont plus proches dans un liquide que dans un gaz.
-
Autre formulation :
-
m =
ρ .
V |
2)- Exercice 06 page 204 : Décrire une propriété des molécules :
|
Décrire une propriété des molécules : Le schéma ci-dessous modélise par des boules les molécules de
dioxygène et de diazote de l’air. 1.
Expliquer ce que représentent les flèches. 2.
Comment cela se traduit-il à l’échelle
macroscopique ?
|
|
Décrire une propriété des molécules :
1.
Les flèches :
-
Les flèches indiquent la direction et
le sens de déplacement de chaque molécule.
-
Elles matérialisent le mouvement des
molécules
-
On remarque que les molécules se
déplacent dans toutes le directions de façon désordonnée.
-
À l’état gazeux règne le chaos
moléculaire.
-
Le schéma représente l’agitation
moléculaire à l’état microscopique 2.
Traduction à l’échelle macroscopique ?
-
Le schéma représente l’agitation
moléculaire à l’état microscopique.
-
À l’échelle macroscopique la grandeur
liée à cette agitation est la température
T de l’air.
-
Lorsque la température augmente,
l’agitation thermique augmente. |
3)- Exercice 08 page 204 : Schématiser une force pressante :
|
Schématiser une force pressante :
-
Représenter la force qu’exerce la
solution sur la paroi du fond du bécher, sans souci d’échelle.
|
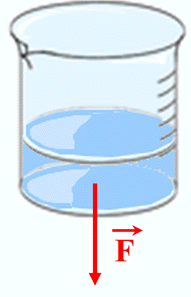
Schématiser une force pressante :
-
Force qu’exerce la solution sur la
paroi du fond du bécher
Point d’application :
on choisit le
centre de la surface pressée
Direction :
perpendiculaire à la paroi
Sens :
orienté du fluide vers la paroi
Valeur : F en newton (N)
-
La valeur
F de la pression dépend
de la pression P du
fluide et de la surface de contact
S
-
Relation : F
= P . S
P :
Pression en N . m–2 ou pascal (Pa)
S :
Surface de contact en m2
F ;
force pressante en newton (N)
![]()
![]()
4)- Exercice 10 page 204 : Force pressante, pression et surface de contact :
|
Force pressante, pression et surface de contact : La relation entre la valeur de la force pressante F, la pression P et la surface S du fluide sur la paroi est : F = P . S. 1.
Pour une valeur de force fixée, comment
varie la pression si la surface de contact est doublée ? 2.
Pour une surface de contact fixée, comment
varie la pression si la valeur de la force est doublée ? 3.
Pour une surface de contact fixée, comment
varie la valeur de la force si la pression diminue de moitié ? |
Force pressante, pression et surface : F
= P . S
P :
Pression en N . m–2 ou pascal (Pa)
S :
Surface de contact en m2
F ;
force pressante en newton (N) 1.
Premier Cas :
-
F’ =
F
-
P’ = ?
-
S’ = 2
S
-
Relation :
-
-
La pression diminue.
-
La pression est divisée par deux lorsque la
surface de contact est multipliée par deux, ceci pour une même force pressante. 2.
Deuxième cas :
-
S’ =
S
-
P = ?
-
F’ = 2
F
-
-
La pression augmente.
-
La pression est multipliée par deux lorsque
la force pressante est multipliée par deux, ceci pour une même surface de contact. 3.
Troisième cas :
-
S’ =
S
-
-
F’ = ?
-
-
La force pressante diminue.
-
La force pressante est divisée par deux lorsque la
pression est divisée par deux, ceci pour une même surface de contact.
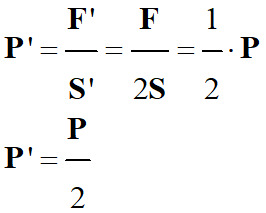
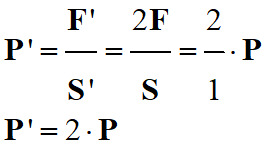
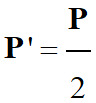
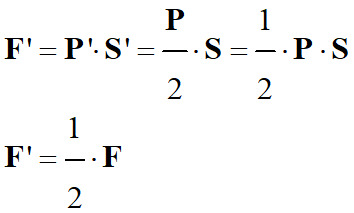
![]()
5)- Exercice 11 page 205 : Calculer la valeur d’une force pressante :
|
Calculer la valeur d’une force pressante : Les deux faces d’une palissade de jardin ont chacune pour surface
S. La pression atmosphérique est notée Patm.
-
Calculer la valeur
F de la force pressante exercée par l’air sur chaque face de cette
palissade.
-
Données :
-
S = 15 × 102 m2
-
Patm = 1,013 × 105
Pa. |
|
Calculer la valeur d’une force pressante :
-
Données :
-
S = 15 × 102 m2
-
Patm = 1,013 × 105
Pa.
-
Valeur F de la force pressante
exercée par l’air sur chaque face de cette palissade
-
F =
F’ =
P . S = 1,013 × 105
× 15 × 102
-
F =
F’ ≈ 1,5 × 108
N |
6)- Exercice 13 page 205 : Étudier une force pressante :
|
Étudier une force pressante : Une force pressante
1.
De quel côté de la vitre se trouve le fluide
exerçant cette force ? 2.
Déterminer la valeur de cette force. |
|
Étudier une force pressante : 1.
Position du fluide exerçant cette force
-
Le fluide au repos se trouve à droite
de la vitre.
-
Schéma :
2.
Valeur de cette force
-
Mesures effectuées sur l’image avec
Photofiltre :
-
Échelles : 10 N ↔ 8,36 cm
-
Longueur du représentant de la
force
-
ℓF ≈ 25,89 cm
-
Valeur de
F :
-
|
7)-Exercice 16 page 205 : Déterminer une différence de coordonnées verticales :
|
Déterminer une différence de coordonnées verticales : On a représenté la différence de pression dans un liquide en fonction de la différence de coordonnées verticales à partir de
mesures obtenues expérimentalement. 1. Déterminer graphiquement la différence zA – zB pour laquelle la différence PB
– PA = 2,70 × 103 Pa. 2.
Montrer que la courbe obtenue est cohérente
avec la loi fondamentale dela statique des fluides :
-
PB –
PA =
ρ .
g (zA
– zB) 3.
Pourquoi les points ne sont-ils pas
parfaitement alignés ? |
|
Déterminer une différence de coordonnées verticales : 1. Déterminer graphiquement la différence zA – zB pour laquelle la différence PB
– PA = 2,70 × 103 Pa.
-
On peut réaliser une lecture
graphique :
-
(zA
– zB) ≈ 34,5
cm
-
(zA
– zB) ≈ 35 cm 2.
Courbe obtenue et loi fondamentale de la
statique des fluides :
-
Tableau de valeurs :
-
Représentation graphique :
-
Les points sont sensiblement alignés.
-
La courbe obtenue est un segment de
droite qui passe pratiquement par l’origine.
-
L’équation de cette droite est du
type :
-
PB –
PA =
a . (zA – zB)
-
Le terme « a » est le coefficient directeur de la droite tracée.
-
Loi fondamentale de la statique des
fluides :
-
PB –
PA =
ρ .
g (zA –
zB)
-
Schéma :
-
La courbe obtenue est bien en accord
avec la loi fondamentale de la
statique des fluides :
-
Avec :
a =
ρ .
g 3.
Pourquoi les points ne sont-ils pas
parfaitement alignés ?
-
Les points ne sont pas parfaitement
alignés car :
-
Pour effectuer les mesures de
pression, on utilise un manomètre qui possède une classe de
précision.
-
Pour effectuer les mesures des
distances, on utilise une règle graduée au millimètre.
-
Des erreurs sont donc liées à la
précision des instruments de mesures.
|
8)- Exercice 19 page 205 : Lier pression d’un gaz et volume :
|
Lier pression d’un gaz et volume :
Les deux bouteilles ci-dessous contiennent la même quantité de matière de gaz.
-
Quelle est la pression du gaz
dichlore dans la bouteille de droite ? |
Lier pression d’un gaz et volume :
-
Pression du gaz dichlore dans la
bouteille de droite :
-
Bouteille de gauche :
-
Vg = 10 L
-
Pg = 1 × 105
Pa
-
Bouteille de droite :
-
Vd = 10 L
-
Pd = ?
-
Les deux bouteilles sont à la même
température : T = 25 ° C
-
On peut utiliser la loi de Mariotte :
-
À température constante et pour une
quantité donnée de gaz, le produit de la pression
P par le volume V
occupé par le gaz est constant :
-
P . V = k = constante.
-
On peut écrire que :
-
Pg .
Vg =
Pd .
Vd
-

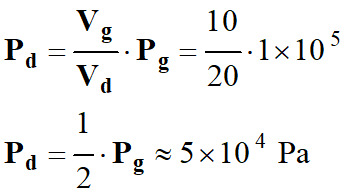
![]()
9)- Exercice 23 page 206 : Pression en plein vol :
|
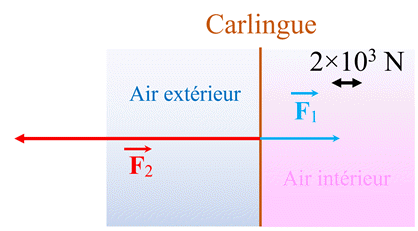
Pression en plein vol : La pression à l’intérieur d’un avion, initialement égale à la pression atmosphérique au niveau du sol, diminue petit à petit lors de la montée pour se stabiliser à 800 hPa lorsque l’altitude de l’avion est supérieure à 2000 m. On étudie un avion volant à l’altitude constante de 10000 m. À cette altitude, la pression atmosphérique est 264 hPa. 1.
Calculer la valeur F1 de
la force pressante exercée par l’air extérieur sur une surface S
de l’avion de 0,20 m2. 2.
Calculer la valeur F2 de
la force pressante exercée par l’air intérieur sur la même surface
S. 3.
On supposera que la surface S est
plane. Représenter, à l’échelle 1 cm ↔ 2 × 103 N les
vecteurs forces
4.
Pourquoi la carlingue d’un avion doit-elle
être rigide ? |
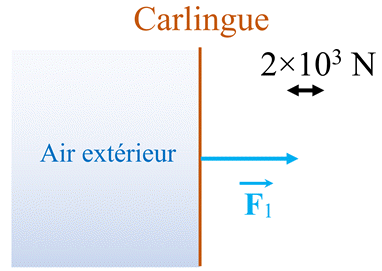
Pression en plein vol : 1.
Valeur F1 de la force
pressante exercée par l’air extérieur sur une surface S de
l’avion.
-
Valeur de la pression :
-
P1 = 264 hPa
-
Valeur de la surface
S :
-
S = 0,20 m2
-
Valeur de la force
F1 :
-
F1 =
P1 .
S = 264 × 102
× 0,20
-
F1 ≈ 5,28
× 103 N
-
F1 ≈ 5,3
× 103 N
-
Schéma :
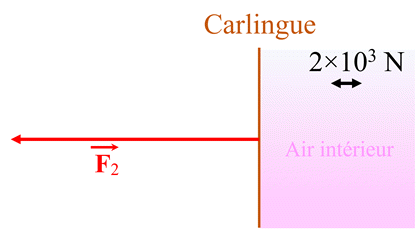
2.
Valeur F2 de la force
pressante exercée par l’air intérieur sur la même surface S.
-
Valeur de la pression :
-
P2 = 800 hPa
-
Valeur de la surface
S :
-
S = 0,20 m2
-
Valeur de la force
F2 :
-
F2 =
P1 .
S = 800 × 102
× 0,20
-
F2 ≈ 1,60
× 104 N
-
F2 ≈ 1,6
× 104 N
-
F2 ≈ 16
× 103 N
-
Schéma : 3.
Représentation, à l’échelle 1 cm ↔ 2 × 103
N, des vecteurs forces
-
Longueur du représentant du vecteur
force
-
ℓF1 ≈ 2,6 cm
-
Longueur du représentant du vecteur
force
-
ℓF2 ≈ 8,0 cm
-
Schéma : 4.
Pourquoi la carlingue d’un avion doit-elle
être rigide ?
-
On peut représenter la résultante
-
Longueur du représentant du vecteur
force
-
ℓF1 ≈ 5,4 cm
-
Valeur de la force
-
FR ≈ 5,4 × 2 ×
103
-
FR ≈ 10,8
× 103
-
FR ≈ 11 × 103
N
-
La carlingue doit être rigide pour ne
pas se déformer sous l’effet de la résultante
![]() et
et![]() .
.![]() :
:![]() :
:
![]()

![]() :
:![]()
![]() des forces pressantes
qui s’exerce sur celle-ci.
des forces pressantes
qui s’exerce sur celle-ci.![]()
10)- Exercice 24 page 206 : Calculer une pression et un volume :
|
Calculer une pression et un volume : Un apnéiste, pour aller explorer les fonds marins, prend une
respiration importante lorsqu’il se trouve à la surface de l’eau puis bloque sa
respiration. Avant de s’immerger, le volume d’air contenu dans ses poumons est V0 = 6,0 L et la pression de l’air a pour valeur celle de la pression atmosphérique : Patm = 1,0 × 105 Pa. On supposera que la pression de l’air dans les poumons de
l’apnéiste est égale à la pression de l’eau qui l’entoure. 1. Les coordonnées verticales des positions de l’apnéiste sont repérées sur un axe Oz orienté vers la haut et dont l’origine est la surface de l’eau. Exprimer la pression P de
l’eau, pour une coordonnée verticale
z, en utilisant la loi fondamentale de la statique des fluides :
-
PB –
PA =
ρ .
g . (zA –
zB) 2.
Pression et profondeur : a.
Calculer la pression P1 de
l’eau lorsque l’apnéiste se trouve à 15 m de profondeur. b.
En déduire, à 15 m de profondeur, la
pression de l’air contenu dans les poumons. 3.
Calculer le volume V1
occupé par cet air à 15 m de profondeur.
-
Données :
-
Masse volumique de l’eau :
ρeau = 1,0 ×
103 kg . m–3
-
Intensité de la pesanteur :
g = 9,81 N . kg–1.
|
|
Calculer une pression et un volume : 1.
Pression P de l’eau pour une
coordonnée verticale z :
-
PB –
PA =
ρ .
g (zA –
zB)
-
Schéma :
-
On applique la loi fondamentale de la
statique des fluides, à l’eau, qui dans le cas présent est un fluide au repos :
-
PB –
PA =
ρ .
g (zA –
zB)
-
En sachant que pour
z = 0, P0 =
Patm
-
P –
P0 =
ρ . g (0 –
z)
-
P =
Patm
–
ρ .
g .
z 2.
Pression et profondeur : a.
Valeur de la pression P1
de l’eau lorsque l’apnéiste se trouve à 15 m de profondeur.
-
Dans ce cas :
-
z1
= – 15 m
-
P =
Patm
– ρ .
g .
z
-
P1 =
1,0 × 105
+ 1,0 × 103 ×
9,81 × 15
-
P1 ≈ 2,47
× 105 Pa
-
P1 ≈ 2,5
× 105 Pa b.
Valeur, à 15 m de profondeur, de la pression
de l’air contenu dans les poumons.
-
On suppose que la pression de l’air
dans les poumons de l’apnéiste est égale à la pression de l’eau qui l’entoure :
-
P =
P1 ≈ 2,5
× 105 Pa 3.
Volume V1 occupé par cet
air à 15 m de profondeur. - On suppose que la température est la même et que la quantité de matière de gaz est la même.
- Ainsi, on peut appliquer la loi de Mariotte :
-
À température constante et pour une
quantité donnée de gaz, le produit de la pression
P par le volume V occupé
par le gaz est constant :
-
P . V = k = constante.
-
On peut écrire que :
-
P0 .
V0 =
P1 .
V1
-
|
|
|