|
|
Cohésion de la matière Exercices |
|
|
|
|
1)- Exercice 04 page 112 : Expliquer la cohésion d’un solide :
|
Expliquer la cohésion d’un solide : Le fluorure de calcium CaF2 (s) est un composé solide dont le modèle ci-dessous représente l’agencement de ses entités constitutives.
-
Déterminer le type d’interaction
assurant la cohésion de cette espèce chimique. |
|
Expliquer la cohésion d’un solide :
-
La fluorine est un cristal ionique
constitué d’un empilement compact et ordonné d’ions calcium
Ca2+ et d’ions fluorure F–.
-
Le cristal est
électriquement neutre, il faut un ion calcium Ca2+
pour deux ions fluorure F–.
-
La formule statistique est
la suivante : CaF2,
-
Le nom :
Le fluorure de calcium.
-
Dans l’écriture de la
formule d’un solide ionique, les charges ne figurent pas.
-
Par convention, on choisit
les plus petits indices qui assurent l’électroneutralité du cristal.
-
La formule statistique
indique la nature et la proportion des ions présents dans le cristal
sans mentionner les
charges.
-
La cohésion du cristal
ionique est due aux forces d’interactions électriques : - Les forces d’attraction électriques entre les ions de signes opposés l’emportent sur les forces de répulsion entre
les ions de même signe. |
2)- Exercice 06 page 112 : Justifier une solubilité :
|
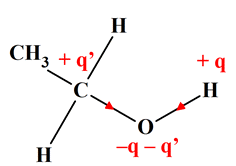
Justifier une solubilité : Les modèles des molécules d’eau et de méthanol sont données, respectivement, ci-dessous :
1.
La molécule de méthanol est-elle polaire ? 2.
Justifier la très grande solubilité du
méthanol dans l’eau. Préciser la nature des
interactions mises en jeu.
-
Données :
-
χ (H)
= 2,2 ;
χ (C)
= 2,6 ;
χ (O)
= 3,4 |
|
Justifier une solubilité :
1.
La molécule de méthanol :
-
L’oxygène est plus électronégatif que
le carbone et l’hydrogène.
-
Les liaisons
C – O et H – O sont
polarisées , alors que les liaisons C
– O sont très peu polarisées. - Il en résulte l’apparition de charges partielles – q et –q’ sur l’atome d’oxygène
et d’une charge partielle (+ q’) sur l’atome de carbone et
(+q) sur l’atome d’hydrogène lié à l’atome d’oxygène.
-
Du fait de la géométrie de la
molécule, les positions moyennes des charges partielles positives (G+) et négatives (G–) ne
sont pas confondues.
-
La molécule de méthanol est polaire. 2.
Solubilité du méthanol dans l’eau.
-
L’oxygène est plus électronégatif que
l’hydrogène : χ (O)
= 3,4 et χ (H) = 2,2
-
Les deux liaisons covalentes O – H
d’une molécule d’eau sont polarisées.
-
Représentation :
- La molécule étant coudée, les positions moyennes des charges partielles positives (G+) et négatives (G–) ne sont pas confondues : - La molécule d’eau
est polaire.
-
L’eau, molécule polaire, est un solvant
polaire.
-
Le méthanol, molécule polaire, est
soluble dans l’eau, solvant polaire.
-
Nature des interactions mises en jeu.
-
La grande solubilité du
méthanol dans l’eau résulte :
-
Des interactions de Van Der
Waals qui interviennent entre les molécules de méthanol et les molécules d'eau ; - Et la formation de nombreuses liaisons hydrogène qui s’établissent entre les molécules de méthanol et les
molécules d'eau.
-
Le
méthanol est soluble à
l’eau en toute proportion.
-
Le méthanol ou alcool de bois
que l'on peut retrouver dans les alcools frelatés.
-
Il provoque la cécité et la mort.
|
3)- Exercice 07 page 112 : Prévoir une solubilité :
|
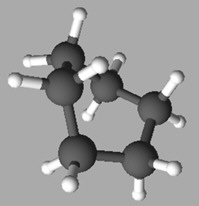
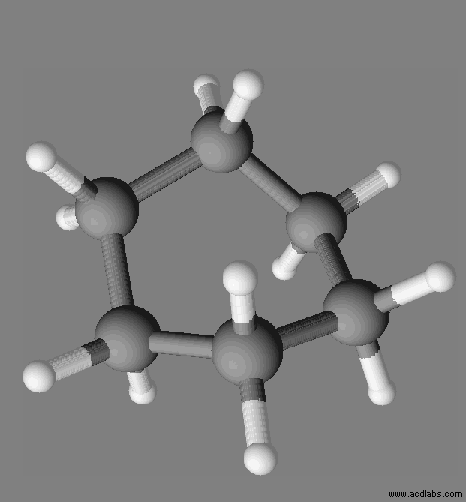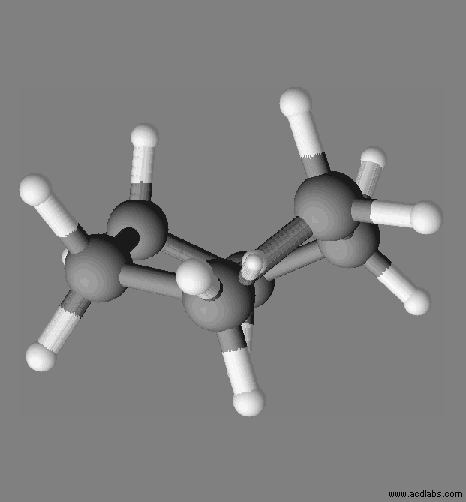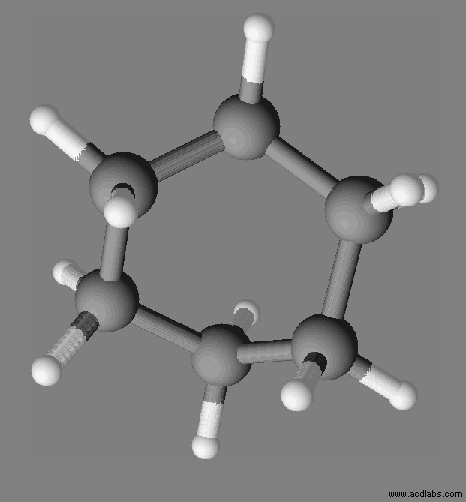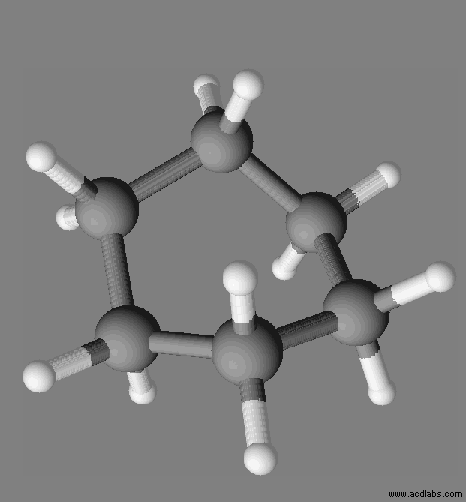
Prévoir une solubilité : Les modèles des molécules d’éthanol CH3CH2OH
et de dibrome Br2 sont données, respectivement,
ci-dessous :
-
De l’éthanol ou du dibrome,
identifier quelle espèce chimique est plus soluble dans le cyclohexane de formule
C6H12.
Justifier.
-
Données :
-
χ (H)
= 2,2 ;
χ (C)
= 2,6 ;
χ (O) =
3,4 ;
χ (Br) = 3,0 |
Prévoir une solubilité :
-
Étude du solvant :
le cyclohexane
C6H12.
-
Les électronégativités du
carbone et de l’hydrogène sont proches :
-
χ
(C) = 2,55 et
χ (H) = 2,2
-
Les liaisons
C
– H,
sont peu polarisées.
-
La molécule de cyclohexane
est apolaire, c’est un solvant apolaire.
-
Étude de la molécule d’éthanol :
-
Du fait de la présence du
groupe –
O – H, l’éthanol est une
molécule polaire.
-
Les liaisons
C
– H,
sont peu polarisées. -
Étude du dibrome :
Br2.
-
Une molécule diatomique constituée de
deux atomes identiques est apolaire.
-
La molécule de dibrome
Br2 est apolaire.
-
Solubilité du dibrome
Br2
-
Le dibrome, molécule apolaire est
soluble dans un solvant apolaire comme le cyclohexane.
-
Alors que l’éthanol, molécule polaire
est très peu soluble dans un solvant apolaire comme le cyclohexane.
![]()
4)- Exercice 08 page 113 : Écrire des équations de réaction de dissolution :
|
Écrire des équations de réaction de dissolution : Le sulfate de baryum BaSO4 (s) est composé
d’ions baryum et d’ions sulfate SO42–. Le sulfate d’argent Ag2SO4
(s) est composé d’ions argent et d’ions sulfate SO42–.
-
Écrire les équations de dissolution
de chacun de ces solides. |
Écrire des équations de réaction de dissolution :
-
Le sulfate de baryum
BaSO4 (s) :
-
Le sulfate de baryum est un solide
ionique.
-
Il est constitué d’un assemblage
compact et ordonné d’ions baryum et d’ion sulfate
SO42–.
-
Il est électriquement neutre.
-
Dans le cristal, il y a autant d’ions
baryum que d’ions sulfate SO42–.
-
Chaque
ion baryum porte une deux charges positives (2+)
-
Formule de l’ion baryum :
Ba2+.
-
Équation de dissolution du sulfate de
baryum : BaSO4
(s)
eau
BaSO4
(s)
→
Ba2+
(aq)
+
SO42–
(aq)
-
Il se présente sous la forme d’une
poudre blanche :
-
Le sulfate d’argent
Ag2SO4
(s):
-
Le sulfate de baryum est un solide
ionique.
-
Il est constitué d’un assemblage
compact et ordonné d’ions argent et d’ion sulfate
SO42–.
-
Il est électriquement neutre.
-
Dans le cristal, il y a deux fois
plus d’ions argent que d’ions sulfate
SO42–.
-
Chaque
ion porte porte une charge positive (+)
-
Formule de l’ion baryum :
Ag+.
-
Équation de dissolution du sulfate de
baryum : Ag2SO4 (s)
eau
Ag2SO4
(s)
→
2 Ag+
(aq)
+
SO42–
(aq)


![]()
5)- Exercice 12 page 113 : Calculer la concentration en quantité de matière d’un ion à partir de la masse d’un solide :
|
Calculer la concentration en quantité de matière d’un ion à
partir de la masse d’un solide : Une solution aqueuse, de volume Vsolution =
150,0 mL, est préparée en dissolvant 500 mg de chlorure de gallium (III), GaCℓ3
(s) dans l’eau. L’équation de la réaction de dissolution est :
1.
Calculer
la quantité de chlorure de gallium (III) dissoute. 2.
Déterminer les quantités de matière n
(Ga3+) d’ions gallium et n (Cℓ–)
d’ions chlorure contenus dans la
solution. 3.
Déterminer les concentrations en quantité de
matière [Ga3+] des ions gallium et [Cℓ–] des
ions chlorure dans la solution.
-
Données :
-
Masses molaires :
-
M (Cℓ)
= 35,5 g . mol–1 ;
M (Ga) = 69,7 g . mol–1 |
|
Calculer la concentration en quantité de matière d’un ion à
partir de la masse d’un solide : 1.
Quantité de chlorure de gallium (III)
dissoute.
-
Masse de chlorure de gallium (III),
GaCℓ3 (s)
dissoute dans l’eau :
-
m = 500 mg
-
Masse molaire du chlorure de gallium
(III), GaCℓ3
(s) :
-
M =
M (Ga)
+ 3 M (Cℓ) = 69,7 + 3 × 35,5
-
M ≈ 176,2
g . mol–1
-
M ≈ 176 g . mol–1
-
Quantité de matière initiale
n0
dissoute de chlorure de gallium (III),
GaCℓ3 (s) :
-
2.
Quantités de matière n (Ga3+)
d’ions gallium et n (Cℓ–) d’ions chlorure
contenus dans la solution.
-
Le mieux est de réaliser un tableau
d’avancement de la réaction :
-
On déduit du tableau d’avancement les
quantités de matière des ions présents dans la solution :
-
n
(Ga3+)
= xmax = n0 ≈ 2,84 × 10–3
mol
-
n
(Cℓ–)
= 3 xmax = 3 n0 ≈ 3 ×
2,84 × 10–3 mol
-
n
(Cℓ–)
≈ 8,513 × 10–3 mol
-
n
(Cℓ–)
≈ 8,51 × 10–3 mol 3.
Concentrations en quantité de matière [Ga3+]
des ions gallium et [Cℓ–] des ions chlorure dans la solution.
-
-
|
|||||||||||||||||||||||||||||||||
6)- Exercice 13 page 113 : Calculer la masse d’un solide à dissoudre :
|
Calculer la masse d’un solide à dissoudre : On veut préparer un volume Vsolution = 50,0 mL d’une solution de phosphate de potassium dont la concentration en quantité de matière des ions potassium est [K+] =
0,30 mol . L–1. L’équation de la réaction de dissolution du phosphate de potassium K3PO4 (s) s’écrit :
1.
Calculer la quantité de matière n (K+)
contenue dans cette solution. 2.
En déduire la quantité de matière n0
de phosphate de potassium à dissoudre pour préparer cette solution. 3.
En déduire la masse m0
correspondante.
-
Données :
-
Masses molaires :
-
M (O)
= 16,0 g . mol–1 ;
M (P) = 31,0 g . mol–1
-
M (K)
= 39,1 g . mol–1 |
|
Calculer la masse d’un solide à dissoudre :
-
[K+]
= 0,30 mol . L–1
-
Vsolution = 50,0 mL 1.
Quantité de matière n (K+)
contenue dans cette solution.
-
n (K+)
= [K+] . Vsolution
-
n (K+)
= 0,30 × 50,0 × 10–3
-
n (K+)
= 1,5 × 10–2 mol 2.
Quantité de matière n0 de
phosphate de potassium à dissoudre pour préparer cette solution.
-
Il faut utiliser le tableau
d’avancement de la réaction :
-
On déduit du tableau d’avancement les
quantités de matière des ions présents
dans la solution :
-
n
(K
+) = 3 xmax
= 3 n0
-
-
Tableau d’avancement :
3.
Valeur de la masse m0
correspondante.
-
m0 = n0
. M (K3PO4)
= 5,0 × 10–3
× (3 × 39,1 + 31,0 + 4 ×16,0)
-
m0 = 1,06
g
-
m0 = 1,1 g
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7)- Exercice 16 page 114 : Choisir un solvant d’extraction adapté :
|
Choisir un solvant d’extraction adapté : On dispose d’une solution de diiode I2 (aq)
photographiée ci-dessous.
-
Déterminer, en justifiant, le solvant
le plus adapté pour réaliser l’extraction du diiode de la solution aqueuse.
-
Données :
|
|
Choisir un solvant d’extraction adapté :
-
Solvant le plus adapté pour réaliser
l’extraction du diiode de la solution aqueuse :
-
On a le choix entre l’éthanol et le
cyclohexane.
-
On doit réaliser une extraction
liquide / liquide :
par un autre
solvant
S2, appelé solvant d’extraction.
-
Le solvant S2
est choisi tel que :
-
L’espèce chimique
à extraire est plus soluble dans le solvant
S2
que dans le solvant S1 ;
-
Le solvant
S2
est non miscible au solvant S1 ;
-
Le solvant
S2
présente un danger minimal pour la santé et l’environnement.
-
Dans le cas présent, le solvant le
mieux adapté est le cyclohexane :
-
Le diiode est soluble dans le
cyclohexane et le cyclohexane est insoluble dans l’eau.
-
Alors que le diiode est soluble dans
l’éthanol, mais l’éthanol est soluble dans l’eau.
-
L’éthanol ne convient pas comme
solvant car il est soluble dans l’eau. |
8)- Exercice 21 page 115 : Solubilité de molécules organiques :
|
Solubilité de molécules organiques : L’éthanol et le pentane sont deux espèces chimiques organiques qui, dans les conditions normales de température et de pression, sont des
liquides incolores. On réalise le mélange de chacun de ces liquides avec de l’eau
colorée en vert.
2.
Interpréter les observations.
-
Données :
-
Électronégativités :
-
χ (H) =
2,2 ;
χ (C) =
2,6 ;
χ (O) =
3,4 ;
-
Modèle de l’eau :
-
Modèle de l’éthanol :
-
Modèle du pentane : C5H12
|
Solubilité de molécules organiques : 1.
Aspect du mélange dans chaque tube à essai.
-
Tube 1 :
-
Mélange eau colorée – pentane :
-
Le mélange est hétérogène :
On observe deux phases.
-
Une phase aqueuse (eau colorée) et
une phase organique (pentane incolore)
-
Tube 2 :
-
Mélange eau colorée – éthanol :
-
le mélange est homogène :
On observe une seule phase :
-
La solution colorée est homogène (mélange de molécule
d'eau et de molécule d'éthanol et de molécules de colorant
vert).
-
Tube 1 :
-
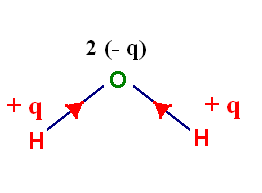
La molécule d’eau :
-
L’oxygène est plus électronégatif que
l’hydrogène : - χ (O)
= 3,4 et χ (H) = 2,2
-
Les deux liaisons covalentes O – H
d’une molécule d’eau sont polarisées.
-
Représentation :
-
La molécule étant coudée, les
positions moyennes des charges partielles positives (G+) et
négatives (G–) ne sont
pas confondues :
- la molécule d’eau est polaire.
-
L’eau molécule polaire, est un
solvant polaire.
-
La molécule de pentane :
-
Les électronégativités du
carbone et de l’hydrogène sont proches :
-
χ
(C) = 2,55 et
χ (H) = 2,2
-
Les liaisons
C
– H,
sont peu polarisées.
-
La molécule de pentane est
apolaire, c’est un solvant apolaire.
-
Conclusion :
-
Le pentane molécule apolaire est
insoluble dans l’eau solvant polaire.
-
On observe deux phases :
-
La phase aqueuse (eau colorée) et la
phase organique (pentane incolore).
-
Le pentane est moins dense que l’eau
et se situe au-dessus de la phase aqueuse.
-
Tube 2 :
-
Mélange : eau colorée et éthanol :
-
Étude de la molécule
d’éthanol :
-
Du fait de la présence du
groupe –
O – H, l’éthanol est une
molécule polaire.
-
Les liaisons
C
– H,
sont peu polarisées.
-
L’éthanol, molécule polaire, est
soluble dans l’eau, solvant polaire. -
La grande solubilité de l'éthanol dans l’eau résulte :
-
Des interactions de Van Der
Waals qui interviennent entre les molécules d'éthanol et les molécules d'eau ;
-
Et la formation de
nombreuses liaisons hydrogène qui s’établissent
entre les molécules d'éthanol et les
molécules d'eau.




![]()
9)- Exercice 24 page 116 : Un traitement de la vigne :
|
Un traitement de la vigne : Le mildiou est une maladie de la vigne provoquée par un
champignon microscopique. L’oxychlorure de cuivre a des propriétés fongicides, dues à l’élément cuivre, qui permettent de lutter efficacement contre le mildiou. C’est un solide ionique qui s’emploie en solution aqueuse, en traitement préventif du mildiou. Il faut, durant tout le cycle de végétation qui dure environ 9 mois, pulvériser une solution aqueuse d’oxychlorure de cuivre tous les quinze
jours sur la vigne. Pour traiter ses vignes, un viticulteur prépare une solution de volume Vsolution = 500 L en dissolvant une masse m0 = 5,00 kg
d’oxychlorure de cuivre Cu2Cℓ(OH)3. Ce dernier utilise cette solution pour traiter une surface de
10,0 hectares (ha).
-
En agriculture biologique, le maximum
toléré est une masse maximale apportée en cuivre égale à 6 kg/ha/an.
-
Le viticulteur peut-il avoir le label
« Bio » ?
-
Données :
-
Masse molaire de l’oxychlorure de
cuivre :
-
M (Cu2Cℓ(OH)3) =
213,5 g . mol–1
-
M (Cu) =
63,5 g . mol–1
-
Formule de l’ion hydroxyde :
HO– |
Un traitement de la vigne :
-
Pour 1 traitement des vignes
sur une surface de 10,0 ha, on utilise une masse m0 d’oxychlorure de cuivre.
-
m0 = 5,00 kg
-
Quantité de matière d’oxychlorure de
cuivre n0
pour 1 traitement :
-
-
L’oxychlorure de cuivre est un solide
ionique.
-
On le dissout dans d’eau.
-
Pour pouvoir connaître la quantité de
cuivre utilisé, il faut écrire l’équation de la réaction de dissolution de l’oxychlorure de cuivre dans l’eau.
-
Dans la solution aqueuse, il y a des
ions cuivre (II) : Cu2+ (aq), des ions chlorure
Cℓ– (aq) et des ions hydroxyde HO– (aq)
-
De plus pour simplifier, on construit
le tableau d’avancement qui lui est associé.
Équation
bilan
eau
Cu2Cℓ(OH)3
→
2 Cu2+
(aq)
+
Cℓ–
(aq)
+ 3 HO– (aq)
État du
système
Avanc.
n (K3PO4)
n
(Cu2+)
n
(Cℓ–)
n
(HO–)
État
initial
x
=
0
n0
0
0
0
État
final
x = xmax
n0
– xmax =
0
2 xmax = 2 n0
xmax = n0
3 xmax = 3 n0
-
Quantité de matière d’ions cuivre
(II) pour 1 traitement :
-
n (Cu2+) =
2 xmax = 2 n0
-
n (Cu2+) ≈
46,8 mol
-
Masse d’ions cuivre (II) pour 1
traitement :
-
m (Cu2+) =
n (Cu2+) . M (Cu2+)
-
m (Cu2+) ≈
2,97 × 103 g
-
m (Cu2+) ≈
2,97 kg
-
Il faut, durant tout le cycle de
végétation qui dure environ 9 mois, pulvériser une solution aqueuse d’oxychlorure de cuivre tous les quinze
jours sur la vigne.
-
Il effectue donc 18 traitements et la
surface traitée est de 10,0 ha.
-
Masse d’ions cuivre (II) m
utilisée pour traiter un hectare de vigne sur l’année :
-
-
m <
6 kg / ha
/ an
-
le viticulteur peut avoir le label
« Bio ».

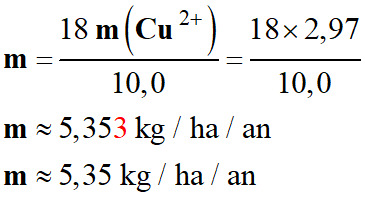
![]()
|
|