I- Dispositif expérimental.

1)- Schéma :

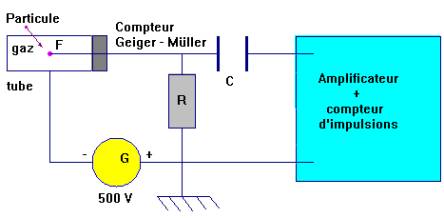
2)- Principe : Le C.R.A.B : Compteur de radioactivité Alpha et Bêta.

-    Le tube est rempli d’un mélange hélium-argon. 

-    Chaque particule (α ou β) qui traverse la fenêtre de mica ionise le gaz qui devient conducteur entre le fil et le cylindre.

-    Il apparaît un micro courant qui est amplifié et détecté.

-  C’est ce qui permet de compter les particules.

-    Ce dispositif peut détecter jusqu’à 10 ⁶ impulsions par seconde.

-    Les impulsions du compteur sont comptées pendant une durée déterminée (on a choisi une seconde).

-    On recommence un grand nombre de fois pour mettre en évidence le caractère aléatoire du phénomène de désintégration.

-    On réalise 1000 comptages de 1 seconde de durée.

-    La source radioactive est placée à 4,5 cm du compteur.

II- Étude préalable.

1)- Écrire les équations des réactions nucléaires qui permettent de justifier l’émission des rayonnements β ^– et γ.

-    le césium 137 est émetteur β ^– :  

2)- Préciser ce que compte exactement le détecteur en faisant la distinction entre le nombre X de particules reçues et le nombre de désintégrations dans la source.

-    Le comptage des désintégrations radioactives d’un échantillon de césium 137 est effectué à l‘aide d’un compteur Geiger – Müller C.R.A.B.

-  (compteur de radioactivité Alpha et Béta).

-    L’échantillon de césium considéré a une activité totale égale à environ 3,0 x 10 ⁵  Bq.

-   Toutes les particules émises ne sont pas détectées.

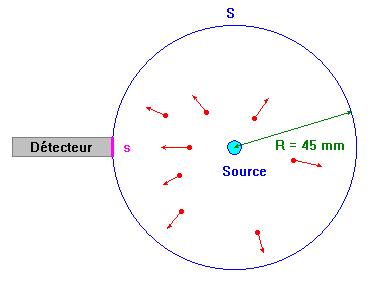
-   En effet la source de césium rayonne dans toutes les directions de l'espace (les particules sont expulsées dans toutes les directions de l'espace).

-    Seules sont détectées les particules qui entrent dans le détecteur par l'ouverture de surface  :  

-     s = π . r ²  

-    (r :  rayon de la fenêtre d'entrée du détecteur).

-    Soit N le nombre de particules émises pendant 1 s. 

-    Ces particules traversent la surface de la sphère de rayon R = 45mm et de surface : 

-    S = 4 π . R ²

-    Le nombre  N_D  de particules détectées est alors tel que :

-    

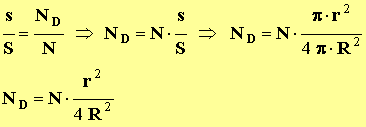
-    Dans l’exemple choisi : r = 3,0 mm et R = 45 mm :

-   

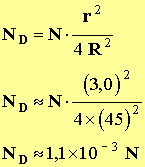
-    Le détecteur ne reçoit qu’une petite quantité du rayonnement émis. D’autre part, l’efficacité du détecteur n’est pas de 100 %. 

Mais on considère que le nombre d’impulsions comptées est proportionnel au nombre de particules émises par la source.  

-    L’activité de la source étant de l’ordre de 3,0 x 10 ⁵  Bq.

-    

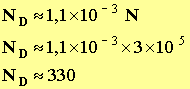
3)- Pour une source donnée, quels sont les paramètres que l’expérimentateur peut modifier et qui influent sur le comptage dans cette expérience ?

-    L’expérimentateur peut intervenir sur la durée du comptage.

-    La distance de la source au détecteur.

-    Il peut placer des écrans de plexiglas, d’aluminium ou de plomb entre la source et le détecteur.

III- Mode opératoire.

-    Placer la source à une distance de 4,5 cm du compteur.

-  Ne plus déplacer la source pendant la manipulation.

-    Choisir une durée de comptage de 1 s et ne plus la modifier.

-    Lancer le comptage en appuyant sur le bouton : ‘’départ comptage’’.

-  Noter le nombre d’impulsions enregistrées par le compteur.

IV- Mesures.

-    Faire d’abord 50 mesures successives et noter les valeurs.

-  Les disposer dans un tableau.

-    n₁ représente la fréquence de l’événement x _i.

-    Faire ensuite n = 50,  n = 200, n = 500…., n = 1000 comptages successifs et noter les valeurs. 

-    Les disposer dans un tableau du même type.

-    Remarque : en mathématique, la grandeur  n_i est appelée fréquence.

-    Remarque : en biologie, la grandeur  n_i est appelée fréquence absolue.

V- Exploitation des mesures.

1)- Tracé des histogrammes.

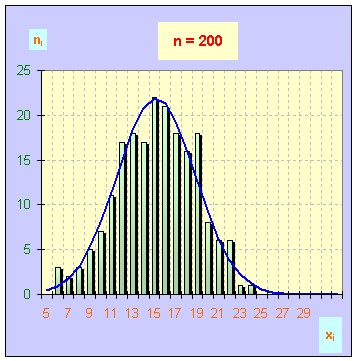
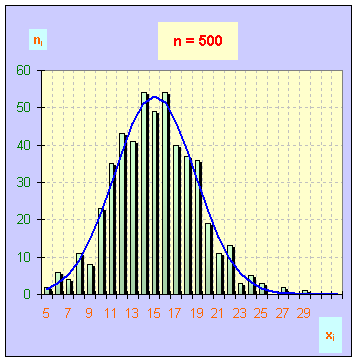
-    Les différents histogrammes : 

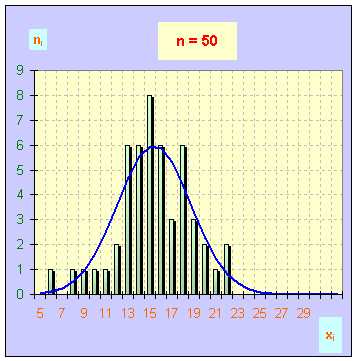
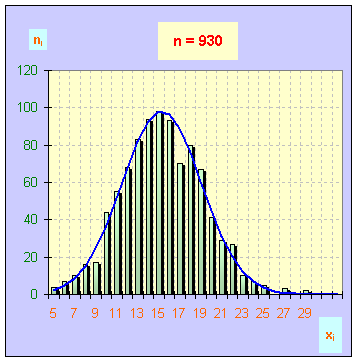
-    Lorsque le nombre de comptages est petit (50), l’histogramme permet de mettre en évidence la valeur la plus fréquente

-    ( x_i = 15 impulsions), mais la loi normale n’est pas respectée.

-    Lorsque le nombre de comptage augmente (n  > 200), la loi normale semble bien suivie. 

-    Pour n = 200, il y a un problème pour x_i = 14 impulsions et x_i  = 19 impulsions. 

-   Ce problème s’estompe lorsque n  > 500.  

- Pour 100 Comptages :

- Tableau de valeurs :

- Graphe associé :

Cliquer sur l'image pour l'agrandir

Cliquer sur l'image pour l'agrandir

-    Ces histogrammes montrent-ils des valeurs régulièrement réparties autour d’une valeur moyenne ? 

-    Qu'en est-il lorsque le nombre de comptage augmente ?

-    Quelles sont les valeurs maximales et minimales du nombre de particules détectées ?

-    Valeur minimale : x_min = 5 et valeur maximale x_max = 29.

-    Quelle est la valeur la plus fréquente ?

-    Valeur la plus fréquente : x _i = 15.

-    Si on effectue une mesure supplémentaire peut-on prévoir sa valeur ? Discuter.

-    On ne peut pas prévoir la valeur du nombre d’impulsions. Mais on peut donner la probabilité pour que x  _i = 15.

-    Lorsque l’on fait un grand nombre de comptage, on s’aperçoit que le phénomène de désintégration est un phénomène purement statistique. 

-    On ne sait pas quels sont les noyaux qui vont se désintégrer mais on peut dire combien. 

-    Un noyau radioactif ne vieilli pas.

2)- Analyse statistique des comptages.

-    Réponses : 

-    On remarque que lorsque n augmente,

-    La probabilité pour que   est de 68 %.

-    La radioactivité est un phénomène purement aléatoire. 

-    l’écart moyen est donné par la relation :

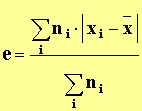
-    Valeur de l’écart moyen :

-    Les paramètres de dispersion σ et e sont liés entre eux σ ≈ 1,25 e.

-   la distribution est pratiquement normale.