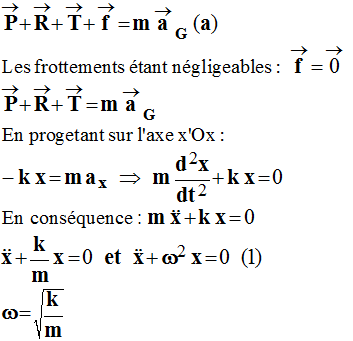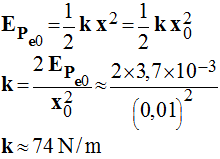|
Phys. N° 18 :
systèmes oscillants.
|
|
|
|
|
I-
Exercice 3 page 301
II-
Exercice 5 page 301
III-
Exercice 7 page 302
IV-
Exercice 11 page 303 |
I- Exercice 3
page 301 :
|
Énoncé : À l’instant t = 0, le centre d’inertie d’un oscillateur élastique non amorti de masse m = 0,20 kg et de constante de raideur k = 50 N / m, a pour abscisse : x0 = 0 et est propulsé avec une vitesse initiale v0x = 2,0 m / s. Il est ensuite animé d’un mouvement rectiligne sinusoïdal d’équation horaire :
x
= xm
cos (ω0
t +
φ) 1)- Calculer numériquement la pulsation et la période. 2)- Donner : a)- L’expression de la vitesse en fonction du temps,b)- L’amplitude et la phase à l’origine des dates.3)- calculer l’énergie mécanique de l’oscillateur. - Comparer l’énergie cinétique maximale à l’énergie potentielle maximale.
|
|
Solution : 4)- pulsation et la période. - L’équation horaire est du type : x = xm cos (ω0 t + φ) solution de l’équation différentielle : -
5)- Donner : a)- expression de la vitesse en fonction du temps -
b)- amplitude et la phase à l’origine des dates. -
-
6)- énergie mécanique de l’oscillateur. -
- Comparer l’énergie cinétique maximale à l’énergie potentielle maximale. -
|
II- Exercice 5
page 301 :
|
Énoncé : Les armatures d’un condensateur chargé sont reliées à une bobine d’inductance L dont l’on néglige la résistance. À l’instant pris comme origine des dates, on ferme l’interrupteur K. L’intensité i (t) du courant dans le circuit est comptée positivement dans le sens indiqué sur le schéma. On note q (t) la charge de l’armature reliée au point A : à l’instant t = 0, cette armature est chargée positivement sous la tension U. 1)- a)- en utilisant la loi des tensions, établir l’équation différentielle donnant les oscillations de la charge du condensateur. b)- pour U = 20 V, C = 2,5 μF et L = 25 mH, montrer que la solution q = 5,0 × 10– 5 cos (4000 t) convient. 2)- Retrouver l’équation différentielle précédente à partir du principe de conservation de l’énergie.
|
|
Solution : 3)- a)- équation différentielle donnant les oscillations de la charge du condensateur. -
b)- la solution q = 5,0 × 10– 5 cos (4000 t) convient. -
4)- équation différentielle précédente à partir du principe de conservation de l’énergie. -
|
III- Exercice 7
page 302 :
|
Énoncé : Oscillateur mécanique amorti : Un corps de masse m forme un anneau autour d’une
tige horizontale (x’x) sur laquelle il peut se
déplacer. Un ressort de raideur k, placé autour de la tige
est fixé à celle-ci en S par une des extrémités et
par l’autre au corps de masse m. Soit O la position du centre d’inertie du corps à
l’équilibre. Schéma :
1)- On écarte le corps d’une longueur x0 à partir de sa position d’équilibre O. Le glissement se produisant sans frottements, établir
l’expression littérale de la pulsation
ω0 des oscillations propres du corps. 2)- Il
existe, en fait, des frottements. On admettra qu’ils se
réduisent à une force
ou
Établir l’équation différentielle caractéristique du
mouvement du corps. Quelle est la nature de celui-ci ? 3)- a)-
Donner l’expression de l’énergie
mécanique par rapport au temps
t et la puissance P de la
force de frottement. b)-
Commenter cette relation en termes
de transfert d’énergie.
|
|
1)- expression littérale de la pulsation ω0. -
2)- équation différentielle avec frottements -
- Nous sommes en présence d’un oscillateur libre amorti. - Suivant la valeur du terme 2. λ, le régime peut être : - pseudo-périodique, - critique - ou apériodique. 3)- Étude énergétique : a)- expression de l’énergie mécanique : -
b)- Relation entre la dérivée de l’énergie et la puissance : -
- Le travail des forces de frottements est transféré vers le milieu extérieur sous forme de chaleur. - Le système perd de l’énergie.
|
IV- Exercice 11
page 303 :
|
Énoncé :
Un solide de masse m est accroché à un ressort de
coefficient de raideur k à spires non jointives. Il peut glisser sans frottement sur un plan horizontal. Le centre de masse G de S est repéré sur un
axe horizontal (x’Ox) dont l’origine correspond à la
position de repos de S.
Un dispositif permet d’enregistrer la variation de x
en fonction du temps. lorsqu’il passe pour la
première fois par l’origine. Quelles sont la période T
et la pulsation ω du mouvement ? 2.
Étude du mouvement du solide : a. Faire le bilan des forces agissant sur le solide : on fera un schéma soigné du système étudié en indiquant l’orientation des forces
et leurs points d’application. b.
Établir l’équation différentielle du
mouvement du solide. Quelle relation existe-t-il entre ω,
m et k ? c.
Déduire du diagramme, l’équation du
mouvement et vérifier qu’elle est bien solution de
l’équation différentielle. 3. Donner l’expression de l’énergie potentielle élastique du ressort à un instant quelconque en fonction de k, x0, ω et t. Sachant que l’énergie potentielle élastique du ressort à l’instant t = 0 est égale à 3,7 × 10–3 J, déterminer la valeur de k. Quelle est la valeur de
la masse m ? |
|
1)- Conditions initiales : Détermination graphique : - Schéma : - x0 = 1,0 cm, - v0 = 0,0 m/s (le solide est lâché sans vitesse initiale) - période du mouvement : T ≈ 0,80 s et ω ≈ 7,85 rad / s 2)- Étude du mouvement : a)- Schéma à l’instant t.
b)- Équation différentielle : - L’amplitude des oscillations étant constante, les frottements sont négligeables. -
c)- Équation du mouvement :- L’équation du mouvement est du type : -
-
-
|
|
|
|
|