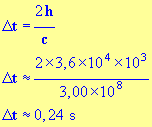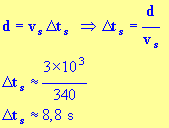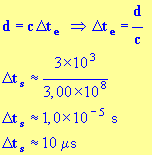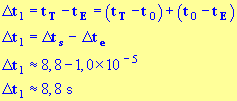|
Correction :
Au cours d’un orage, la foudre tombe à 3 km d’un observateur, en
provoquant au même instant noté
t0 un coup de tonnerre et un éclair.
a)- Combien de temps va-t-il s’écouler entre l’instant
t0 et l’instant où l’observateur entend le tonnerre ?
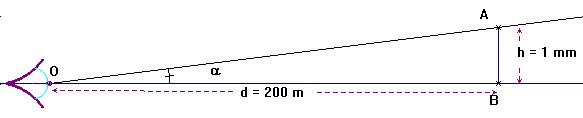
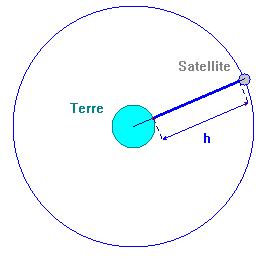
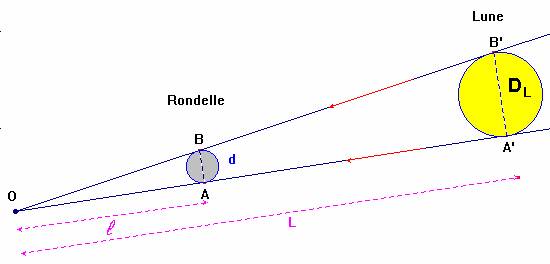
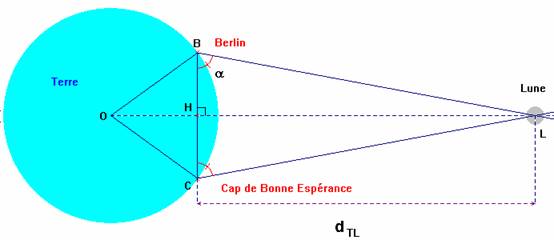
- Schéma de la situation :
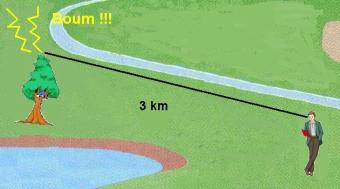
- Notations : à l’instant
t0 (date): coup de tonnerre et éclair.
- On note
tT, l’instant (date) où
l’observateur entend le tonnerre.
- On note
tE, l’instant (date) où
l’observateur voit l’éclair.
- La célérité de l’onde sonore :
vs = 340 m / s
- La célérité de l’onde lumineuse :
c
= 3
× 10 8 m
/ s.
- On note la durée entre l’instant
t0 et
tT :
Δts =
tT -
t0.
- On note la durée entre l’instant
t0 et
tE :
Δte =
tE -
t0.
- Durée entre l’instant
t0 et l’instant tT où l’observateur entend le tonnerre.
-
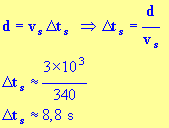
b)- Combien de temps va-t-il s’écouler entre l’instant
t0 et l’instant où l’observateur voit l’éclair ?
- Durée
entre l’instant
t0 et l’instant tE où l’observateur voit l’éclair.
-
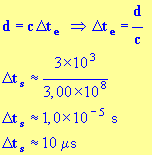
c)- Combien de temps s’écoule-t-il entre le moment où il voit l’éclair
et le moment où il entend le tonnerre ?
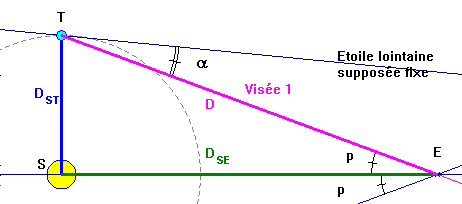
- Schéma de la situation :
-
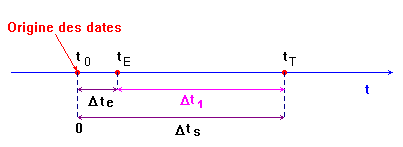
- Durée entre le moment
tE
où il voit l’éclair et
le moment
tT
où il entend le tonnerre :
- 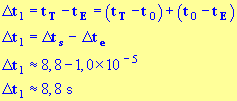
- En conséquence :
Δt1
≈
Δts
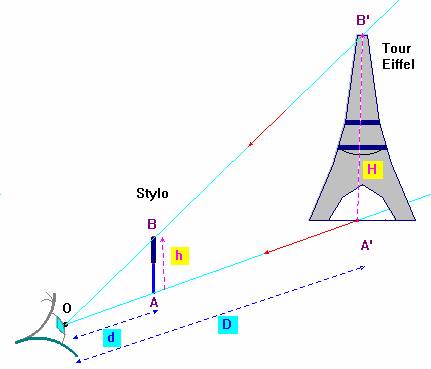
d)- En déduire que, pour calculer l’ordre de grandeur de la distance à
laquelle la foudre est tombée,
on peut compter les secondes qui séparent la
vision de l’éclair du coup de tonnerre et diviser ce nombre par 3 pour
obtenir la distance en kilomètre.
- Pour parcourir 3 km, la durée est de 9 s environ.
- Le son met pratiquement 3 s pour parcourir 1 km.
-
La vision de l’éclair
est instantanée.
-
Elle permet de déclencher le décompte du temps.
|

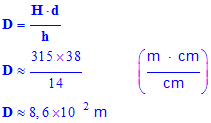
 (1)
(1)
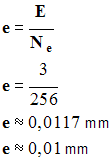
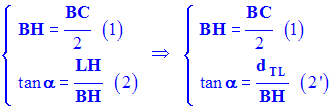
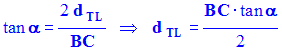
 .
.