Correction 

I- Expérience et enregistrement.

1)- Dispositif utilisé informatique et mécanique.

-  Une balle est lancée avec une vitess e faisant un angle α avec le plan horizontal.

-  On réalise une étude chronophotographique du mouvement de la balle.  

-  La Webcam est située dans un plan perpendiculaire à l’axe de visée.

2)- Obtention de l’enregistrement sur papier.

-  Ouvrir le logiciel d’acquisition et de traitement vidéo : aviméca 2.7.

-  Clique sur l’icône :  et dans le dossier vidéo, choisir le fichier : parabil, parabil1 ou parabille.

-  Choisir comme échelle de la vidéo : 250 % pour plus de précision.

-  Repérer les différentes positions de la bille au cours de son mouvement à l’aide du pointeur .

-  On choisit le repère d’Espace :

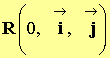
-  Cliquer sur l’icône Étalonnages :

-  Remarque : il faut choisir des teintes claires pour les points lors du pointage et pour les axes. 

-  Puis, il faut prendre des teintes foncées pour les points et les axes lors du collage (on peut prendre la teinte noire).

-  Pour le collage : Cliquer sur l’icône ,

-  Ouvrir un document Word, choisir l’orientation paysage et coller.

-  Faire un double clic sur l’image et choisir la taille suivante pour l’image,

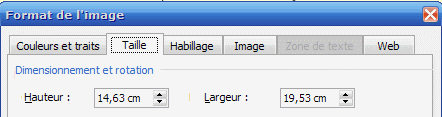
-  Pour cette taille, l’échelle est la suivante : Échelle : 10 cm ↔ 1,0 m.

-  On peut lancer l’impression (imprimante de la salle B130).

II- Repère d'espace et repère de temps.

1)- Introduction.

-  On note G₁ la première position occupée par le centre d’inertie G de la bille. 

-  On choisit comme origine des espaces, la position G₁₀ et comme origine des dates, l’instant où le mobile occupe la position G₁₀.

-  Indiquer les propriétés du clip vidéo.

-  Sur le tracé, indiquer le repère d’Espace, l’origine des espaces et l’échelle utilisée.

-  Quelle est le référentiel d’étude ? Est-il galiléen ? Justifier.

-  Compléter le tableau suivant :

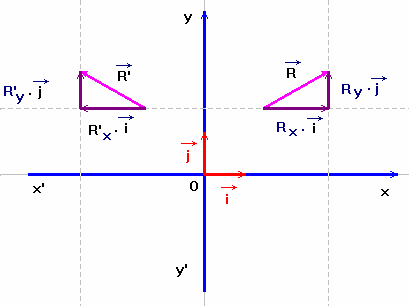
2)- Coordonnées cartésiennes d'un vecteur.

-  Pour connaître les coordonnées cartésiennes d'un vecteur, on projette ce vecteur sur les axes Ox et Oy.

-    Remarque : R_x et R_y sont des grandeurs algébriques.

3)- Le vecteur vitesse.

-  Détermination de la valeur de la vitesse instantanée.

-  Soit i  =  4, 6, 15 et 17  l'indice du point choisi : Les instants t_{i – 1} et t _{i + 1} encadrent l'instant t _i.

Mesurer la distance parcourue par le mobile : G_{i – 1} G_{i + 1}.

- Déterminer la durée de parcours Δt.

-  En déduire la valeur de la vitesse v_Gi.

►Tracé du vecteur vitesse.

-  Tracer la parallèle issue du point G_i à la droite (G_{i – 1} G_{i + 1}).

-  Donner la longueur du représentant ℓ_vi du vecteur vitesse. On utilise l'échelle : 1 m / s  ↔  2 cm.

-  Idem pour les autres indices. On peut présenter les résultats sous forme d’un tableau.

Déterminer les coordonnées cartésiennes de chaque vecteur vitesse. vérifier les valeurs.

III- Force et variation de vitesse.

1)- bilan des forces extérieures appliquées un solide.

Faire le bilan des forces extérieures appliquées au solide.

-  Faire un schéma de la situation à l’instant t.

-  Représenter les actions mécaniques à partir du point G. On considère que les frottements sont négligeables.

-  En déduire les caractéristiques de la résultante

-  Donner les coordonnées de dans le repère

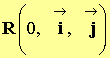
2)- Vecteur variation du vecteur vitesse de G aux temps t₅ et t₁₆.

-    Pour t₅ :

Tracer le vecteur à partir du point G₅. Que représente ce vecteur ?

Que peut-on dire du vecteur variation du vecteur vitesse de G et de la résultante  des forces extérieures ?

-  Pour t₁₆ : Idem.

IV- Le vecteur accélération.

1)- Introduction.

2)- Détermination de la direction et du sens du vecteur accélération aux temps t₅ et t₁₄.

Tracer le représentant du vecteur à partir de G_i.

-  Le vecteur accélération a même direction et même sens que le vecteur

3)- Détermination de la valeur a_i du vecteur accélération au temps t_i.

Mesurer la longueur du représentant de

-  À l'aide de l'échelle, donner la valeur de Δv_G en m / s.

-  Diviser Δv_G par  Δt  = 2 τ et en déduire la valeur de l'accélération a_i. Attention aux unités.

-  En quelle unité s’exprime la valeur de l’accélération ?

4)- Tracer le vecteur : Échelle : 1 m / s²  ↔ 0,50 cm.

Déterminer les coordonnées cartésiennes du vecteur accélération.

5)- Conclusions.