|
TP Physique N° 08 bis |
Établissement du courant dans une bobine 2004 : Correction |
|
|
|
|
Programme 2012 : Physique et Chimie Programme 2020 : Physique et Chimie |
Matériel : bobine, source de courant ; conducteur ohmique de 18 Ω ; ordinateur ; carte CANDIBUS
|
Mettre en évidence le retard à l'établissement du courant et le phénomène d'auto-induction dû à une bobine dans un circuit. Détermination de la valeur de l'inductance propre d'une bobine par différentes méthodes. |
WinLabo2

1)- Montage :
Il comprend : Un générateur idéal de tension E = 3,2 V ; un conducteur ohmique de résistance R’ = 18 Ω,
une bobine d’inductance L et de résistance r = 8,8 Ω et un interrupteur K.
Au temps t = 0 s, on ferme l’interrupteur en le basculant sur la position 1.
Remarque dans cette expérience, E = 3,23 V

Au temps t = 0 s, on ferme l'interrupteur K :

1)- Étude quantitative de la courbe : uBM = g (t)
a)- Visualisation de uBM = g (t) :
- Courbe expérimentale obtenue :
- uBM = g (t) et uBM = R'.i
- Au cours du temps, la tension uBM augmente , il en va de même pour le courant d'intensité i.
- Le courant met un certain temps pour s'établir dans le circuit.
- Il existe
- Un régime transitoire : établissement du courant
- Un régime permanent : lorsque le courant est établi.
- Durée de la première phase : Δt ≈ 8,0 ms (environ).
b)- Déduire de la courbe la valeur maximale de la tension U0 aaux bornes du conducteur ohmique lorsque le régime permanent est atteint.
Réponse : U0 ≈ 2,10 V
c)- Déterminer la valeur de la tension U0L aux bornes de la bobine lorsque le régime permanent est atteint.
- E = uL + uR' - Lorsque le courant est établi : -
uBM =
U0 =
2,10 V
et
uAB
=
U0L. - U0L = E − U0 - U0L = 3,23 − 2,10 - U0L
≈ 1,13 V
|
d)- Donner la durée
Δt au bout de
laquelle
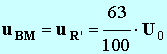 . Que représente
Δt
?
. Que représente
Δt
?
- Δt ≈ 1,38 ms
- Cette valeur représente une valeur approchée de la constante de temps du circuit (R, L).
- L'enregistrement ne commence que lorsque la tension aux bornes du conducteur ohmique n'est supérieure ou égale à 0,30 V.
- Il y a un décale dans le temps, on le voit bien sur l'enregistrement expérimental.
- Δt ≈ τ ≈ 1,38 ms
2)- Étude de la courbe : i = h (t)
a)- Visualisation de la courbe : iexp = h (t)
b)- Déterminer la valeur du courant I0 dans le circuit lorsque le régime permanent est atteint.
- I0 ≈ 0,117 A
c)- Donner l'expression littérale de la loi d'ohm aux bornes de la bobine et aux bornes du conducteur ohmique.
- Loi d'Ohm aux bornes de la bobine :
- 
- Loi d’Ohm aux bornes du conducteur ohmique :
- uR
=
uBM
= R'.i
- Pour aller plus loi : -
- d)- Que peut-on dire de la valeur
- En déduire la valeur de la résistance totale
R du circuit. Comparer R et r + R'
. - Conclusion. 
![]() de lorsque le régime permanent est atteint ?
de lorsque le régime permanent est atteint ?
- Application
numérique :
-
- R =
(r + R')
-
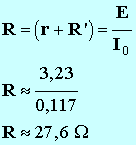
- Calcul d'erreur :
-

e)- Sachant que la constante de temps du circuit (R, L) :
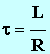 et que d'autre part,
τ
=
Δt
:
voir la questionn :
(IV-1)-d))),
et que d'autre part,
τ
=
Δt
:
voir la questionn :
(IV-1)-d))),
-
- Par la suite, on détermine une valeur de L par une autre méthode
plus précise et qui tient compte du décalage temporel au départ. a)- - Même
remarque que précédemment : ceci est seulement une valeur approchée de
l'inductance.
- Même
remarque que précédemment : ceci est seulement une valeur approchée de
l'inductance.
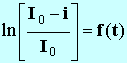
-
On remplacee I0 par Iex au numérateur car autrement un message d’erreur s’affiche lorsquee i = I0.-
entrer les valeurs dee Iex et de I0. Si un message d'erreur apparaît : augmenter la valeur dee Iex.- Placer le curseur dans la colonnee
D.|
Cliquer sur Variable, Puis sur Ajouter
|
|
Taper la formule :
ln(I
ex– i) / I
0 Dans cet exemple, I ex = 0,137 Aet I0 = 0,136 A
et
|
b)- Visualisation de la courbe
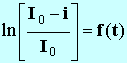 .
.|
Cliquer sur l’icône
|
|
Mettre t en abscisses ( X)Et ln en ordonnées (Y)
et
|
b)- Exploitation de la courbe obtenue.
- Quelles sont les caractéristiques de la courbe obtenue ?
- On travaille sur le domaine qui est pratiquement
rectiligne et on calcule le coefficient directeur du segment de droite.
- Pour
ce faire, avec le pointeur, on relève les coordonnées de deux points du
segment de droite. - On utilise : - On trouve :
-
-
- a' est l'inverse d'un temps et a' est
négatif.
-
- On
peut trouver l'expression dee i
= h
(t). -
4)- Vérification à l'ordinateur : tracé de la courbe : i = h (t) à
l'ordinateur. - L'enregistrement ne commence que lorsque la tensionn
uR est supérieure ou égale à 0,30 V ( ou 0,017 A).
- C'est pour cette
raison que la courbe théorique est décalée dans le temps par rapport à la courbe
expérimentale..
- Si l'on remplacee
T par (T + 0,00020).
- La
courbe théorique et la courbe expérimentale se superposent parfaitement.
V
- Étude complémentaire..
-
Donner l'expression de
-
Tracer la tangente à la courbe
à t = 0. Quel est son coefficient directeur ? Que représente-t-il ?
-
En déduire la valeur de la constante de tempss
τ
du circuit. - - Comparer les
différentes valeurs de L trouvées par les différentes méthodes.
-
Conclusions.
- - - - - 


![]()
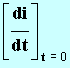 en fonction dee
I0 et t
.
en fonction dee
I0 et t
.
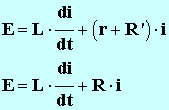

-
τ
≈
1,72 ms
- -
La
valeur de l'inductancee
L annoncée par le constructeur est : L = 45 mH. - Calcul d'erreur : 
