Moteur de recherche

I- But :

-  Détermination de la célérité du son dans l’air à une température donnée.

-  Mesure d’un retard d’une salve d’ultrasons à l’aide d’un oscilloscope.

II- Mesure de la célérité d’un son dans l’air.

1)- Dispositif expérimental.

-  L‘expérience est assistée par ordinateur.

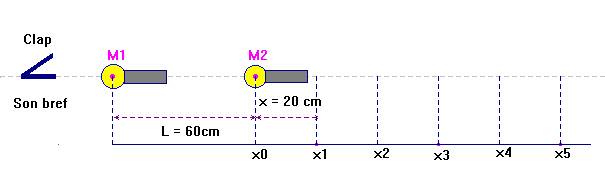
-  Schéma :

-  Réglage des différents paramètres : la température, le nombre d’acquisitions, la longueur x et le nombre de mesures pour chaque distance.

2)- Principe de la mesure.

Un son bref est émis. Il se propage et atteint le premier micro M₁ (micro fixe). 

Ce micro est relié à un dispositif électronique qui déclenche le chronomètre. 

Le son continue à se propager et atteint le deuxième micro M₂ (micro mobile). 

Le deuxième micro est relié à un dispositif électronique qui provoque l’arrêt du chronomètre.

Pour la distance L, le temps mesuré noté t₀ est donné en μs.

Pour la distance L + x, le temps mesuré noté t₁ est donné en μs

Pour la distance L + 2 x, le temps mesuré noté t₂ est donné en μs.

…………………………………………………..

On effectue plusieurs mesures (5) pour une même distance. Comme valeur, on prend la valeur moyenne des mesures pour une même distance..

Décrire le principe de la mesure. Pourquoi effectue-t-on plusieurs mesures pour une même distance ? Pourquoi utilise-t-on cette méthode différentielle ?

3)- Mesures.

Reproduire et compléter le tableau suivant :

4)- Exploitation.

Sur papier millimétré, tracer x (cm) = f (t). 

-  Quel type de graphe obtient-on ? 

-  Tracer la droite moyenne. 

-  Calculer son coefficient directeur. 

-  Que représente-t-il ? 

-  Donner son unité dans le (S.I).

-  En déduire la valeur expérimentale v_exp de la célérité du son dans l’air.

Comparaison avec la valeur théorique. À 0 °C = 273 K, la célérité du son dans l’air est de 331, 45 m / s. 

-  On admet que la célérité du son dans l’air est proportionnelle à la racine carrée de la température absolue T.

-  Donner la relation liant la vitesse du son à une température donnée T. 

-  En déduire la valeur de la vitesse du son v _th à la température de la salle.

-  Comparer la valeur expérimentale avec la valeur théorique. Conclusion.

III- Mesure d’un retard pour une salve ultrasonore.

1)- Dispositif expérimental.

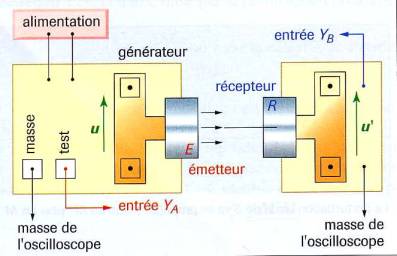
Schématiser le montage et le réaliser.

2)- Mesures.

Figure 1.	Fugure 2.

  Mettre en place l’émetteur ultrasonore et le récepteur. 

Observer l’écran de l’oscilloscope lorsque l’émetteur est en mode salve 

(Une salve ultrasonore est une perturbation sonore de fréquence supérieure à 20 kHz séparée par une durée réglable.)

-  Fixer la règle et déplacer le récepteur R pour obtenir sur l’écran de l’oscilloscope la disposition de la figure 1.

-  Placer le zéro de la règle à la position du récepteur R quand l’écran montre la figure 1.

-  Déplacer lentement le récepteur R en observant l’écran jusqu’à ce que le début de la salve soit décalé d’une division. 

-  Lorsque le récepteur R est dans la position de la figure 2, la déformation reçue a un retard τ par rapport à la déformation reçue dans la position de la figure 1.

-  Repérer la position du récepteur sur la règle : d = .

3)- Exploitation.

-  Grâce à la durée de balayage de l’oscilloscope, déduire la valeur du retard τ . 

-  À quel parcours des ultrasons le retard t correspond-il ? 

-  En déduire la célérité des ultrasons dans l’air. 

-  Comparer cette valeur à celle trouvée précédemment. 

-  Conclusion.