|
Phys. N°06 |
Le circuit RC : Exercices. Correction. |
|
|
|
|
Programme 2012 : Programme 2020 : |
I- Applications.
Pour aller plus loin :
|
Mots clés : Récepteur et générateur ; convention récepteur ; convention générateur ; le circuit électrique ; orientation d'un circuit électrique ; loi d'Ohm ; le conducteur ohmique ; résistance d'un conducteur ohmique ; le condensateur ; capacité d'un condensateur ; charge et décharge d'un condensateur ; énergie d'un condensateur ; constante de temps d'un circuit RC ; ... |
|
Un dipôle RC est constitué d’un
conducteur ohmique de résistance R = 2,7 kΩ et d’un condensateur
de capacité C = 10–7 F. La constante de temps du circuit vaut :
a)- 2,7 ×
10– 7 s ;
b)- 2,7 ×
10 4 s ; c)- 0,27 ms ; |
|
- La constante de temps τ d’un circuit RC est donnée par la relation : τ = RC . réponse c)-. - τ = 2,7 × 10–3 × 10–7 - τ = 2,7 × 10–4 s - τ ≈ 0,27 ms |
|
Un condensateur de capacité C = 0,50 μF est chargé pendant une durée t = 3,5 s. Le générateur délivre un courant électrique d’intensité constante I = 0,60 mA. a)- Calculer la charge accumulée sur l’armature positive. En déduire la charge accumulée sur l’armature négative. b)- Combien vaut la tension aux bornes du condensateur ? |
|
a)- Charge accumulée sur l’armature positive et charge accumulée sur l’armature négative. - Schéma du circuit :
- Charge accumulée sur l’armature positive. - qA = I . t - qA = 0,60 × 10–6 × 3,5 - qA ≈ 2,1 × 10–6 C - qA ≈ 2,1 μC - Charge accumulée sur l’armature négative. - À chaque instant : - qA = – qB ≈ 2,1 μC b)- Combien vaut la tension aux bornes du condensateur ? - Tension aux bornes du condensateur. -
|
|
L’expression de la tension aux bornes d’un condensateur est de la forme :
a)- Préciser la signification et l’unité de chaque terme. b)- Quelle est la valeur de u(t) à t = 0 s ? Lorsque t → ∞ ? Le condensateur se charge-t-il ou se décharge-t-il ? c)- Donner l’expression de la charge q (t) du condensateur. d)- En déduire celle de l’intensité i (t) dans le dipôle RC. e)- Quelle est la valeur de l’intensité en régime permanent ? |
|
a)- Signification et l’unité de chaque terme. - Schéma du montage :
- u (t) tension aux bornes du condensateur : volt V. - U constante qui représente la valeur de l’échelon de tension volt V. - Le temps t en seconde s. - La constante de temps du circuit RC : t en seconde s. b)- Valeur de u (t) à t = 0 s ? Lorsque t → ∞ et état du condensateur - Valeur de u (t) à t = 0 s : -
- Expression que l’on peut mettre sous une autre forme : -
-
- Valeur de u (t) lorsque τ → ∞ : -
- Lorsque l’on ferme l’interrupteur K au temps t = 0 s, le condensateur se charge. c)- Expression de la charge q (t) du condensateur. - Expression de la charge q (t) du condensateur : (voir schéma)
-
d)- Expression de l’intensité i (t) dans le dipôle RC. - Intensité du courant électrique dans le circuit avec l’orientation choisie : -
e)- Valeur de l’intensité en régime permanent. - Valeur de l’intensité en régime permanent : c’est-à-dire lorsque le régime permanent est atteint. - Dans l’expression trouvée précédemment, on fait tendre le temps t vers l’infini. -
- En conséquence, lorsque le condensateur est chargé, l’intensité du courant électrique dans le circuit est nulle.
|
|
Dans le circuit ci-dessous, on ferme l’interrupteur K à l’instant t = 0 s. Le condensateur est initialement déchargé. - Schéma :
a)- Quelle est la valeur de la tension uAB aux bornes du condensateur à t = 0 s ? Lorsqu’il est chargé ? b)- Exprimer la tension uBD aux bornes du conducteur ohmique de résistance R en fonction de R, C et uAB. c)- En déduire l’équation différentielle vérifiée par uAB(t). d)- La solution de cette équation différentielle est du type : uAB (t) = k1 + k2 . e–k t avec k, k1 et k2 constantes. En considérant la valeur de u AB pour t = 0 s et lorsque t → ∞, déterminer l’expression de uAB(t). e)- Vérifier que uAB (t) est bien solution de l’équation différentielle établie à la question c)-. f)- À partir de uAB (t), établir les expressions de q (t) et i (t).
|
|
- Schéma :
a)- Valeur de la tension uAB aux bornes du condensateur à t = 0 s et lorsqu'il est chargé - Valeur de la tension uAB aux bornes du condensateur à t = 0 s : - Le condensateur est déchargé au temps t = 0 s : uAB (0) = 0 V.- Lorsque le condensateur est chargé : uAB (∞) = E. b)- Expression de la tension uBD aux bornes du conducteur ohmique de résistance R - Tension uBD aux bornes du conducteur ohmique de résistance R en fonction de R, C et uAB. - Loi d’Ohm aux bornes du conducteur ohmique : - Schéma du circuit avec l’orientation choisie.
- 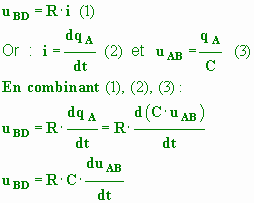
c)- Équation différentielle vérifiée par uAB (t) : - Additivité des tensions : -
d)- Solution de l’équation différentielle :- Les conditions initiales permettent d’écrire que : - u AB (t) = k1 + k2 . e – k × 0 => k1 + k2 = 0 => k1 = – k2 (1)
- uAB (t) = k1 + k2 . e– k t - uAB (t) = E - E . e– k t - uAB (t) = E . (1 – e– k . t) - Il reste à déterminer l’expression de k. - On utilise le fait que uAB (t) est solution de l’équation différentielle :
-
- Cette équation est vérifiée ceci quel que soit t. En conséquence, il faut que :
-
- Expression de uAB (t ) : -
e)- Vérifier que uAB (t) est bien solution de l’équation différentielle établie à la question c)-. - Vérification : -
- Cette équation est vérifiée ceci quel que soit t. f)- À partir de uAB (t), établir les expressions de q (t) et i (t). - Expressions de qA (t) :
-
- Expressions de i (t) : -
|
|
Charge d’un condensateur. Pour étudier la charge d’un condensateur, on réalise un circuit RC que l’on soumet à un échelon de tension E. Grâce à l’oscilloscope, on observe simultanément : La tension uR aux bornes du conducteur ohmique de résistance R (Ajustée à R = 200 Ω) ; - La tension uC aux bornes du condensateur. 1)- Quelle tension permet de connaître les variations de l’intensité du courant en fonction du temps ? Justifier. 2)- La masse du générateur est isolée de la Terre. Il est ainsi possible de brancher la masse de l’oscilloscope comme indiquée sur la figure. On obtient l’oscillogramme ci-dessous.
Afin de mieux distinguer les deux courbes, l’une est décalée vers le haut et l’autre vers le bas, avec les réglages : - Base de temps (ou durée de balayage) : 0,5 ms / div ; - Sensibilité verticale de la voie A et de la voie B : 2 V / div ; - Entrée B inversée. a)- Identifier les deux courbes. b)- Compléter le circuit en indiquant les connexions à réaliser avec l’oscilloscope. c)- Déterminer à l’aide de l’oscillogramme : 3)- La constante de temps τ est définie comme la durée au bout de laquelle le condensateur initialement déchargéatteint 63 % de sa charge maximale. a)- Déterminer la valeur de τ. b)- Déterminer par analyse dimensionnelle l’expression correcte de cette constante parmi les relations suivantes : c)- en déduire une valeur approchée de la capacité C du condensateur. 4)- Pour les mêmes réglages du générateur et de l’oscilloscope, on augmente la valeur de la résistance R du conducteur ohmique. a)- Les grandeurs E, Imax et t sont-elles modifiées ? Si, oui, dans quel sens ? b)- L’oscillogramme ci-dessous représente l’allure de la tension aux bornes du condensateur pour R pour une augmentation de R et pour une diminution de R. à quel cas correspond chacune des courbes ?
5)- On augmente la valeur de l’échelon de tension E, les grandeurs I max et τ sont-elles modifiées ? Si oui, dans quel sens ? |
|
Charge d’un condensateur. 1)- Tension qui permet de connaître les variations de l’intensité du courant en fonction du temps et justification - Schéma :
- Avec l’orientation choisie, on peut écrire la loi d’Ohm aux bornes du conducteur ohmique : - uMB = uR = R . i - La tension aux bornes du conducteur ohmique de résistance R permet de visualiser les variations de l’intensité du courant en fonction du temps ceci à une constante près. -
2)- Oscillogramme :
a)-
Identifi - La courbe 1 visualise les variations de la tension uR en fonction du temps (c’est-à-dire les variations de i en fonction du temps). - La courbe 2 visualise les variations de la tension uC en fonction du temps. - Lorsque l’on charge un condensateur avec un échelon de tension, l’intensité dans le circuit diminue et s’annule lorsque le condensateur est chargé. - La tension aux bornes du condensateur augmente et devient maximale et égale à E lorsque le condensateur est chargé. b)- Circuit et connexions à réaliser avec l’oscilloscope. - Schéma :
- À la voie 1 ou A (YA) de l’oscilloscope, on visualise la tension uAM. - C’est la tension aux bornes du condensateur de capacité C. -
Avec l’orientation choisie :
ceci à une constante près. - À la voie 2 ou B (Y B) de l’oscilloscope, on visualise la tension uBM. - Avec l’orientation choisie, uBM = – uR = – R . i. - Pour visualiser les variations de i, à une constante près, il faut appuyer sur la touche – B ou B ‘’inversée’’. - Cela revient à visualiser uMB = – uBM = R.i. c)- Déterminer à l’aide de l’oscillogramme : - tension E entre les bornes du générateur :
- uAMmax = E = k . y - uAMmax = E = 2 × 2 - uAMmax = E ≈ 4 V - La valeur maximale Imax de l’intensité du courant qu’il débite. - Valeur maximale Imax de l’intensité du courant qu’il débite.
-
3)- La constante de temps τ est définie comme la durée au bout de laquelle le condensateur initialement déchargé atteint 63 % de sa charge maximale. a)- Déterminer la valeur de τ. - Constante de temps du circuit RC. -
- Détermination graphique : -
- En utilisant l’oscillogramme, on peut donner une valeur approchée de la constante de temps τ du circuit RC. - Ici, on trouve que τ ≈ 0,25 ms. - Cette méthode à l’aide de l’oscillogramme n’est pas très précise mais elle donne un ordre de grandeur de la valeur de τ. b)- Déterminer par analyse dimensionnelle l’expression correcte de cette constante parmi les relations suivantes : -
- Analyse dimensionnelle : -
-
-
- La bonne relation est : τ = RC c)- Valeur approchée de la capacité C du condensateur : -
4)- On augmente la valeur de la résistance R du conducteur ohmique. a)- Les grandeurs E, Imax et t sont-elles modifiées - Lorsqu’on augmente la valeur de la résistance du conducteur ohmique, la valeur E de l’échelon de tension reste inchangée. - La valeur Imax diminue et la constante de temps t augmente. b)- L’oscillogramme ci-dessous représente l’allure de la tension aux bornes du condensateur pour R pour une augmentation de R et pour une diminution de R. à quel cas correspond chacune des courbes ?
- La courbe 2 correspond à R = 200 Ω.
-
La courbe 1 correspond à R < 200 Ω, la constante de
temps est plus petite, le condensateur se charge plus vite.
-
La courbe 3 correspond à R > 200 Ω, la constante de
temps est plus grande, le condensateur se charge plus lentement. 5)- On augmente la valeur de l’échelon de tension E, les grandeurs I max et τ sont-elles modifiées ? Si oui, dans quel sens ? - Lorsque l’on augmente la valeur de l’échelon de tension E, I max augmente et la constante de temps τ du circuit ne change pas.
|