I -But. II - Etude préliminaire. III - Mesures des valeurs d'un échantillon de résistances à l'ohmmètre. IV - Utilisation du code des couleurs. V - Mesure d’une résistance avec un seul ohmmètre. Incertitude due à l’appareil. VI - Conclusions. VII - Notions de statistiques descriptives pour une variable (Se qu'il faut connaître)

I- But :

-  Prendre conscience que l’écart à la moyenne est insuffisant pour décrire la dispersion des valeurs.

-  Introduire la notion d’écart type et de variance.

-  Remarque : La dispersion des valeurs rend compte de la répartition des valeurs par rapport à la valeur moyenne.

II- Étude préliminaire :

1)- Choix de l ‘échantillon.

-  Pour l’étude préliminaire et pour introduire des notions de statistiques, on travaille sur un échantillon d’âges dans un groupe de personnes.

2)- Terminologie.

-  L’âge est désigné par x. Un âge particulier par x_i L’indice i représente le numéro de l’âge dans la liste.

-  Exemple : x₁ = 39 ; x₅ = 48 ……

-  Le nombre total de valeurs de la liste est n. Ici n  = 10.

3)- Effectif d’une valeur.

-  on appelle effectif  n_i le nombre de fois où une valeur x _i apparaît dans la liste.

-  Exemple : quelle est l’effectif de la valeur 39 ?

-  La valeur 39 apparaît deux fois ; son effectif est n₁ =  2.

4)- Moyenne arithmétique .

-  La moyenne arithmétique est le quotient de la somme des valeurs x_i par le nombre n.

-  On écrit :

- 

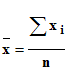
-  Explication : En mathématique, une somme est représentée par la lettre grecque ( lettre sigma en majuscule).

5)- Écart à la moyenne de chacune des valeurs.

-  Notation : l’écart à la moyenne de chacune des valeurs est notée :

-  Reproduire et compléter le tableau suivant :

6)- La variance : var.

-  La variance var est le quotient de la somme des carrés des écarts à la moyenne par le nombre n de l’effectif total.

- 

-  Calculer la variance de l’échantillon :  var  ≈  204

7)- L’écart-type.

-  L’écart-type σ est égal à la racine carrée de la variance.

-  L’écart-type caractérise la dispersion des valeurs.

-  Affirmation : En mathématique, on constate que l’intervalle contient plus de la moitié des valeurs de la liste.

Calculer la valeur de l’écart-type σ : 

Calculer les bornes de l’intervalle .

Compter le nombre de valeurs comprises dans cet intervalle. L’affirmation est-elle vérifiée ?

8)- Représentation par un diagramme en barres ou histogramme.

-  En abscisse, on fait figurer les valeurs de la liste et en ordonnée l’effectif de chaque valeur.

-  On trace un ensemble de segments (ou rectangles) verticaux.

-  Faire apparaître sur le graphique l’abscisse de la moyenne arithmétique et les bornes de l’intervalle .

III- Mesure des valeurs d’un échantillon de résistances avec un ohmmètre.

1)- Matériel et principe.

-  On utilise des ‘’résistances’’ vendues par un fabricant comme des résistances de valeur 1 kΩ  connue à 1 % près. 

-  Elles sont ‘’livrées’’ en bandes de 7, 8 ou 10 que l’on évite de défaire pour réaliser les mesures. 

-  Les binômes échangent les différentes bandes et  travaillent sur un échantillon de 100 résistances.

-  Par la suite, on va faire une étude statistique des valeurs de la résistance de cet échantillon.

-  Pour effectuer la mesure de la valeur de chaque résistance, on utilise un multimètre transformé en ohmmètre.

2)- Préparation du multimètre.

Configurer le multimètre pour mesurer une résistance dont la valeur est voisine de 1 kΩ . 

-  Indiquer les étapes suivies : (on utilise les sondes spéciales)

-  Étape 1 :……………………………………………………………………………………………………………

-  Étape 2 :……………………………………………………………………………………………………………

-  Étape 3 :……………………………………………………………………………………………………………

3)- Mesures et saisie des valeurs.

-  Ouvrir le dossier MPI et sur le fichier Excel : TP MPI n° 09 élèvesZ.zip.

-  Le fichier  possède trois feuilles de calcul  et  s’ouvre à la feuille de calcul :  mesures.

Tableau de valeurs : 

-  Il faut entrer les valeurs mesurées les unes à la suite des autres dans le tableau bleuté (plage A5 : T9). Il faut entrer des valeurs entières.

-  Lorsque le tableau est rempli, il faut déterminer la valeur maximale et la valeur minimale de la résistance de l’échantillon. 

-  On utilise des formules spécifiques qui permettent de simplifier et accélérer le travail.

4)- Effectifs des valeurs des résistances de l’échantillon.

-  On travaille dans la feuille de calcul :  ‘’mesures’’

-  Le but de cette étape est de déterminer l’effectif, noté n_i de chaque valeur, notée x_i de la résistance de l’échantillon.

-  Dans la cellule E11 (jaune) taper la formule : =MAX(A5:T9) puis

-  Dans la cellule E13 (bleue) taper la formule : =MIN(A5:T9) puis

-  À partir de la cellule D17 (verte), faire varier la valeur de R de sa valeur minimale à sa valeur maximale en augmentant d’une unité.

-  Pour déterminer la valeur de l’effectif n _i pour chaque valeur x _i de R,

-  taper la formule suivante dans la cellule D18 (orange) : =NB.SI($A$5:$T$9;D17) puis 

-  Remarque : pour faire le point, utiliser la combinaison des touches ‘’MAJ + . ‘’ du clavier.

-  Recopier la formule vers la droite pour compléter le tableau : sélectionner la cellule D18 (orange). 

-  Déplacer la souris vers le coin droit en bas de la cellule jusqu’à ce qu’un plus (+) noir apparaisse. 

-  Tout en maintenant le clic gauche, déplacer la souris vers la droite tant que cela est nécessaire.

-  Reproduire le tableau des effectifs des valeurs de l’échantillon.

-  Quelles sont les observations que l’on peut faire ?

5)- Moyenne arithmétique des valeurs des résistances de l’échantillon.

-  Calculer la moyenne arithmétique en utilisant l’ensemble des valeurs du tableau bleuté. 

-  Taper la formule suivante dans la cellule F26 (jaune) :  =MOYENNE(A5:T9) puis 

-  Calculer la moyenne arithmétique en utilisant les effectifs.

-  Taper la formule permettant de la calculer dans la cellule F29 (verte)  : =D20/H22 puis 

-  Justifier ce calcul et donner la formule permettant de calculer la moyenne arithmétique

-  à partir des effectifs  des valeurs des résistances de l’échantillon.

6)- Variance de l’échantillon des valeurs.

-  On travaille dans la feuille de calcul :  ‘’var’’

-  Relation :

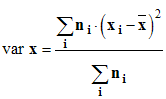
-  Calculer la variance de l'échantillon de valeurs :

-  Première étape : Calculer .

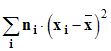-  Dans la cellule D5 (jaune) , taper la formule : =SOMME(D4:T4) puis 

-  Deuxième étape : Diviser le résultat de la cellule D5 par l'effectif total.

-  Dans la cellule H11 (verte), taper la formule : =D5/H7 puis 

-  Remarque 1 : on peut faire le calcul en une seule étape. Proposer une solution.

-  Remarque 2 : La cellule K11 (blanche) affiche la valeur de la variance de l'échantillon de mesure grâce à une formule interne d'Excel.

-  Comparer les valeurs trouvées dans les cellules K11(blanche) et H11(verte).

7)- Écart-type.

-  Calculer l'écart-type de l'échantillon de valeurs :

-  Dans la cellule H21 (bleue), taper la formule : =RACINE(H11) puis 

-  Remarque : dans la cellule K21 (blanche), On affiche l'écart type grâce à une formule interne d'Excel,

-  Comparer les valeurs trouvées dans les cellules K21 (blanche) et H21 (bleue).

-  Donner l'encadrement des valeurs de R sachant que  x - σ  < R  < x + σ.

-  Il faut utiliser la feuille de calcul et travailler avec les cellules H28 (rose)  et L28 (orange).

-  Dans la cellule H28 (rose), taper la formule : =H9-H21 puis 

-  Dans la cellule L28 (orange), taper la formule : =H9+H21 puis 

-  Quel est le nombre n, de valeurs de résistance, qui appartient à l’intervalle x - σ  < R  < x + σ ?

-  Quelle conclusion peut-on tirer quant à la dispersion des valeurs de la résistances de l’échantillon ?

8)- Histogramme.

-  On travaille dans la feuille de calcul :  ‘’hist’’

-  Tracer l’histogramme des effectifs en fonction des valeurs de R à l’aide du Tableur.

-  Commenter l'allure de l'histogramme obtenu.

-  Que peut-on dire de la répartition des valeurs de R de l'échantillon ?

fichier complet

IV- Utilisation du code des couleurs.

1)- Les contraintes du fabricant.

-  Le fabricant est tenu de respecter le cahier des charges. 

-  Les conducteurs ohmiques possèdent un anneau de tolérance. 

-  La couleur de cet anneau indique la tolérance sur la valeur de la résistance donnée par les autres anneaux de couleur.

-  Donner l’encadrement des valeurs de R prévu par le fabricant.

2)- Comparaison et conclusion.

-  Comparer cet encadrement avec celui trouvé à la question III- 7) -.

-  Que peut-on dire des deux encadrements ? Le fabricant a-t-il respecté le cahier des charges ?

V- Mesure d’une résistance avec un seul ohmmètre. Incertitude due à l’appareil.

1)- Utilisation de la documentation technique du multimètre.

-  Le fabricant d’appareils de mesure est tenu de tester son matériel. 

-  Il donne des indications à l’utilisateur dans une notice technique le plus souvent en termes d’incertitude relative exprimée en %.

-  Chercher dans la documentation technique du multimètre utilisé de quoi compléter le tableau suivant :

-  Remarque : 

-  Dans ces documentations techniques, on voit des données telles que ± 0,3 % de la valeur lue ± un digit ou Unité de Représentation (UR).

-  Ce ‘’digit’’ ou ‘’UR’’ est une unité qui correspond au dernier chiffre affiché.

-  Exemple : Si la fiche technique annonce 2 UR sur le calibre utilisé et que l’affichage donne : 0.123. 

-  Cela correspond à une incertitude sur la mesure de ± 0,002.

-  Exemple : sur le calibre utilisé, la fiche technique annonce ± 0,3 % de la valeur lue ± 2 UR.

-  L’affichage donne 0,996. La valeur lue est R _lue = 0,996 kΩ.

-  L’incertitude absolue :

-

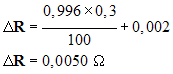
-  L’encadrement de la valeur de R : 0,991 Ω  <  R  < 1,001 Ω. 

2)- Mesure de la valeur de la résistance.

-  Utiliser une résistance de 1 kΩ utilisée précédemment (sans l’extraire de la bande).

-  Calculer l’incertitude absolue notée ΔR d’après les renseignements fournis par la documentation.

-  À partir de la mesure effectuée de cette résistance, donner l’encadrement de la valeur R _lue autorisé par la notice de l’appareil.

-  Cet encadrement est-il inclus dans celui trouvé préalablement ? Dans celui prévu par le fabricant ?

VI- Conclusions.

Classer les propositions suivantes en facteur positif (P), négatif (N) ou sans influence (O) sur la qualité d’une mesure :

►  Une seule mesure est suffisante.

►  On n’utilise qu’un seul appareil de mesure.

►  On recommence un grand nombre de fois la même mesure avec le même appareil.

►  On recommence un grand nombre de fois la même mesure avec des appareils différents.

►  On refait la même mesure en changeant de manipulateur.

►  On prend l’appareil le plus cher.

►  On se fie à la notice du constructeur de l’appareil.

-  Conclure sur les conditions d’une « bonne mesure ».

-  Toutes les mesures sont entachées d’erreurs pour diverses raisons examinées dans les 3 cas précédents.

-  Le résultat d’une mesure est généralement plus ou moins sûr.

-  La valeur exacte ou vraie nous demeure inconnue.

-  Afin de préciser numériquement cette incertitude, on écrit, pour la grandeur mesurée A :

- 

Complément : 

Fichier Excel compressé :

Code des résistances zip :

Code des résistances zip

VII- Notions de statistique descriptive pour une variable.

1)- Population : c’est l’ensemble étudié. Les éléments de l’ensemble sont appelés unités statistiques.

2)- Échantillon : c’est un sous-ensemble quelconque de la population. Si l’échantillon est prélevé au hasard, c’est un échantillon aléatoire.

3)- Caractère : c’est l’aspect de l’unité statistique auquel on s’intéresse.

Il peut être qualitatif (couleur d’une voiture) ou quantitatif (valeur de la résistance d’un conducteur ohmique) : il se traduit alors par un nombre.

4)- Valeur statistique ou valeur du caractère : la valeur du caractère est sa mesure lorsque l’on a choisi une unité.

On obtient des valeurs de la variable statistique.

5)- Variable discrète : elle ne peut prendre que des valeurs isolées.

On convient d’ordonner ces valeurs dans l’ordre croissant.

6)- Variable continue : elle peut prendre n’importe quelle valeur d’un intervalle.

7)- Effectif : l’effectif de x_i est le nombre d’observations n_i associé à la valeur x_i de l’intervalle statistique.

8)- L’effectif total :

9)- Série statistique : c’est l’ensemble des couples ( x_i ; n_i ). On donne souvent cette série sous forme d’un tableau statistique.

10)- Fréquence : .

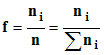11)- La dominante ou mode : c’est la valeur du caractère la plus fréquente.

12)- La moyenne : c’est le quotient de la somme des mesures par l’effectif total.

-      

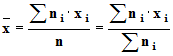
13)- La médiane : c’est une valeur de x_i  telle que l’effectif des valeurs inférieures à cette valeur est égale à la moitié de l’effectif total.

14)- L’étendue : c’est la différence entre la plus grande et la plus petite des valeurs observées.

15)- La variance : elle est égale à la moyenne des carrés diminuée du carré de la moyenne.

- 

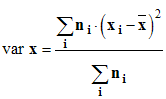
-  Formule de Kœnig :

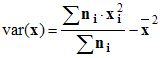
-  Il s’agit d’évaluer les écarts de chaque valeur de x_i  à la valeur moyenne .

16)- L’écart-type : C’est la racine carrée de la variance :

-  Si représente la moyenne, σ  l‘écart-type et x une valeur incluse dans l'ensemble de données, alors

-  environ 68 % des données se situent à l'intérieur de l'intervalle :

-  environ 95 % des données se situent à l'intérieur de l'intervalle :
-  Environ 99 % des données se situent à l'intérieur de l'intervalle :