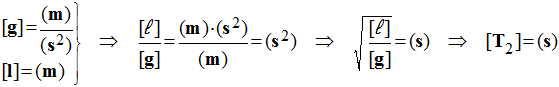I- Les Pendules de Galilée.

 

"J'ai pris deux boules, l'une de plomb et l'autre de liège, celle-là au moins cent fois plus lourde que celle-ci, puis j'ai attaché chacune d'elles à deux fils très fins, long tous deux de quatre coudées ; les écartant alors de la position perpendiculaire, je les lâchais en même temps (…) ; une bonne centaine d'allées et venues accomplies par les boules elles-mêmes, m'ont clairement  montré qu'entre la période du corps pesant, et celle du corps léger, la coïncidence est telle que sur mille vibrations comme sur cent, le premier n'acquiert sur le second aucune avance, fût-ce minime, mais que tous deux ont un rythme de mouvement rigoureusement identique. On observe également l'action du milieu qui, en gênant le mouvement, ralentit bien davantage les vibrations du liège que celles du plomb, sans toutefois modifier leur fréquence ; même si les arcs décrits par le liège n'ont plus que cinq à six degrés, contre cinquante à soixante pour le plomb, ils sont en effet traversés en des temps égaux."

 

Les pendules de Galilée peuvent être assimilés à des pendules simples.

1)- Dans le cas d'un pendule simple, qu'appelle-t-on oscillation ? Quelles sont les deux expressions employées dans le texte pour désigner une oscillation ?

-  Une oscillation du pendule simple correspond au mouvement entre deux passages successifs par la même position, dans le même sens, c'est un aller retour.

-  Les deux expressions employées dans le texte : "allée et venue", "vibration".

2)- Un pendule simple présente une position d'équilibre. Comment Galilée la désigne-t-il ?

-  Galilée désigne la position d'équilibre par "la position perpendiculaire". Galilée écarte les pendules de la position perpendiculaire pour les mettre en mouvement.

3)- Le texte permet-il de montrer que la période T du pendule simple dépend ou non :

a)-  De la masse m de la boule ?

-  Galilée compare la période d'un pendule simple de longueur ℓ et de masse m avec celle d'un pendule de même longueur et de masse différente (la boule de liège et la boule de plomb).

-  On lit dans le texte : "… qu'entre la période du corps pesant, et celle du corps léger, la coïncidence est telle que sur mille vibrations comme sur cent, le premier n'acquiert sur le second aucune avance".

-  En conséquence, la période des oscillations du pendule simple est indépendante de la masse.

b)-  De la longueur ℓ du fil ?

Justifier les réponses. Si le texte ne permet pas de répondre, proposer une expérience permettant de montrer l'influence de l'une ou de l'autre des grandeurs précédentes.

   

-  Le texte ne donne aucune information concernant la longueur du fil puisque les deux pendules ont la même longueur.

-  L'expérience complémentaire, consiste à fabriquer deux pendules avec deux boules de même masse mais de longueur différentes et de mesurer leur période.

4)- On propose les expressions suivantes pour la période :

  où  g = 9,8  m / s²

a)-  à partir du texte, quelles expressions de la période doit-on éliminer ?

-  Comme la période T est indépendante de la masse m, on peut éliminer les expressions où la masse intervient :

 - 

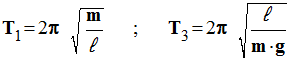
b)-  Par analyse dimensionnelle, choisir l'expression correcte de la période.

-  La période T est homogène à un temps, elle s'exprime en seconde.

-   

-  En conséquence, T₂ est homogène à un temps, alors que T₄ ne peut pas être homogène à un temps, T₄ est homogène à la racine carrée d'une longueur.

-  L'expression 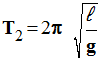est la bonne.

a)- Calculer la période des pendules utilisés par Galilée. La coudée sera prise égale à 50 cm et g = 9,8  m / s².

-  Période des pendules de Galilée :

-   

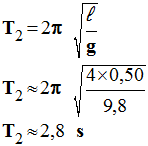
5)- On suppose que toutes les causes d'amortissement sont négligeables.

Les deux pendules sont écartés d'un même angle par rapport à leur position d'équilibre.

à l'instant t₀ = 0 s, on les lâche sans vitesse initiale.

a)-  Les pendules ont-ils même énergie cinétique au passage par leur position d'équilibre ? Justifier la réponse.

-  Les deux pendules ont "un rythme de mouvement rigoureusement identique", à chaque instant, ils ont la même vitesse.

-  Ayant des masses différentes, ils n'ont pas la même énergie cinétique.

b)-  Que dire de l'énergie mécanique au cours du mouvement ?

-  Étant donné que toutes causes d'amortissement est négligeable, l'énergie mécanique du système

-  S = {pendule, fil, Terre} se conserve.

 

II- Le pendule élastique.

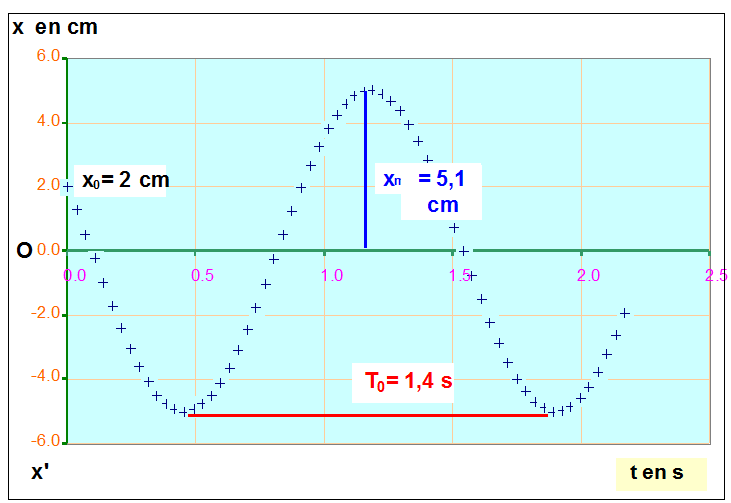
L'enregistrement ci-dessous est celui de l'élongation x d'un oscillateur élastique horizontal (raideur du ressort k et masse du mobile m = 536 g).

Le ressort a sa longueur naturelle lorsque x = 0.

1)- Déterminer la période propre T₀ des oscillations. En déduire la pulsation propre ω₀ des oscillations.

-  Période propre des oscillations :

-   

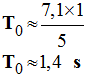
-  Pulsation propre :

-   

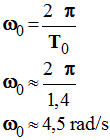
2)- Déterminer l'amplitude x_m des oscillations. Déterminer la raideur k du ressort.

-  Amplitude des oscillations :

-   

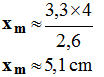
-  Raideur du ressort :

-   

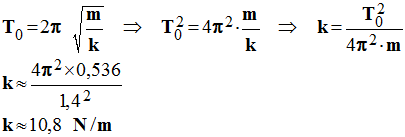
3)-  En utilisant le modèle suivant : x = x_m cos(ω₀ . t + φ), déterminer la phase φ à l'origine des dates.

 

-  Phase à l'origine des dates :

-  x₀ = 2 cm et x_m = 5,1 cm.

 

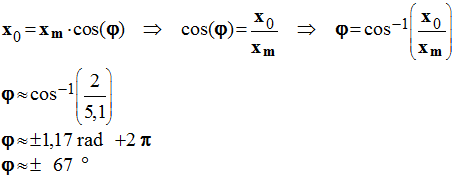
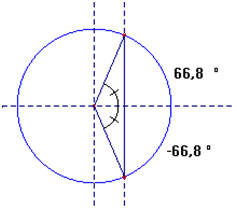
-  La vitesse permet de choisir la bonne solution :