I- Mouvement parabolique.

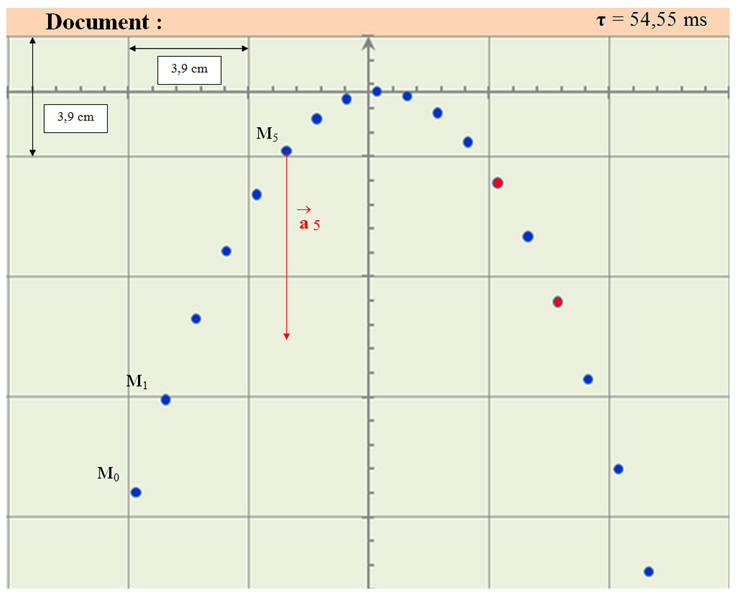
On enregistre, avec diginum, la trajectoire parabolique du centre d’inertie d’un mobile autoporteur de masse m = 536 g, sur un plan incliné d’un angle α = 7,0 ° par rapport à l’horizontale.

Pour cela, le mobile est lancé vers le haut et parallèlement au plan incliné, avec une vitesse initiale v₀ = 0,81 m / s qui fait l’angle θ = 73,5 ° avec la ligne de plus grande pente.

On enregistre ainsi la position du centre d’inertie du mobile à intervalles de temps τ = 54,55 ms.

On obtient l’enregistrement suivant.

Document :

1)- Quel est le référentiel utilisé ? Est-il Galiléen ? Préciser le repère de temps choisi ? Quel est le repère d’espace choisi ? (utiliser les données du document joint)

-    Référentiel : la table à digitaliser qui est liée à la Terre. C’est par rapport à la table à digitaliser que l’on étudie le mouvement du mobile. C’est un référentiel terrestre supposé Galiléen

-    Repère de temps : origine des temps : instant ou le mobile occupe la position O (sommet de la parabole) et l’unité de temps : la seconde

-    Repère d’Espace : lié au référentiel d’étude :

-    La position O (sommet de la parabole) est l’origine des espaces :

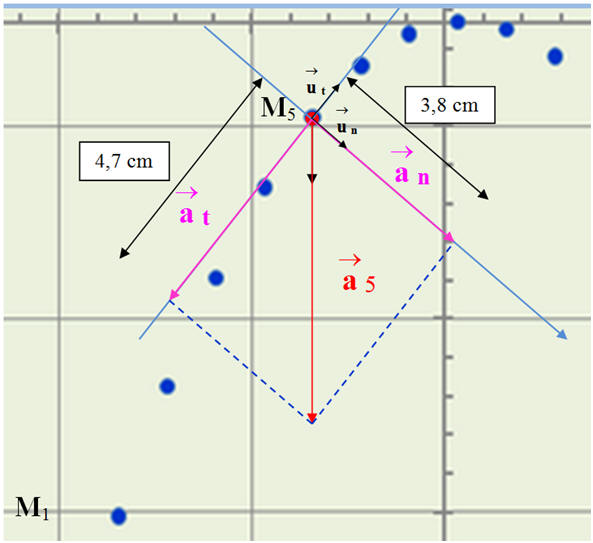
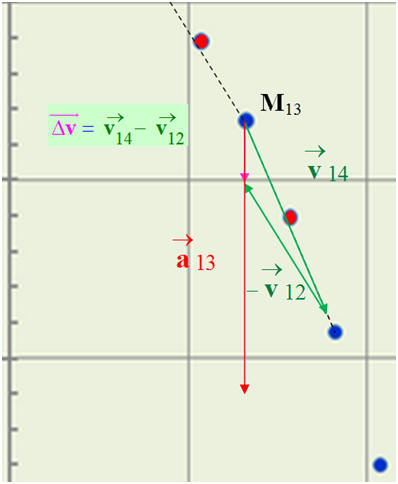
2)- Construction graphique du vecteur accélération.

a)-  construire graphiquement le vecteur accélération . Faire apparaître les éléments de la construction. Donner la valeur a₁₃  de l’accélération.

 

-    construction  graphique le vecteur accélération . (Échelle pour les vecteurs vitesse 0,10 m / s ↔ 1 cm)

-     

-     

-     

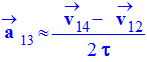
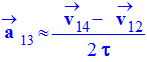
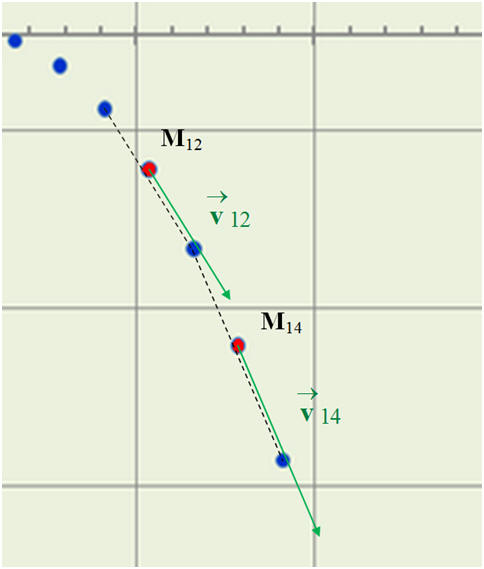
-    Tracé des vecteurs vitesses :

 

 

 

-    On trace 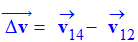 à partir du point M₁₃.

-    Le représentant du vecteur 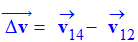 mesure 1,34 cm.

 

 

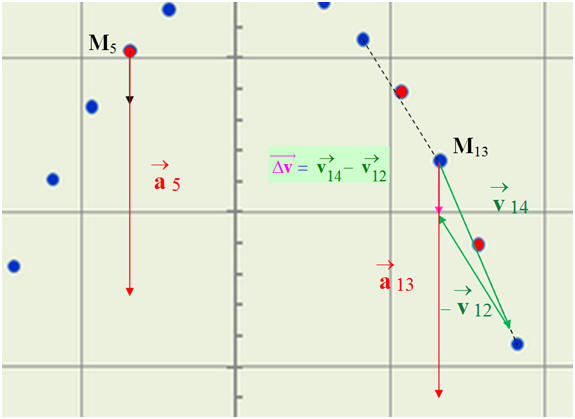
-    On en déduit la valeur du vecteur variation  du vecteur vitesse : Δv ≈ 0,13 m / s

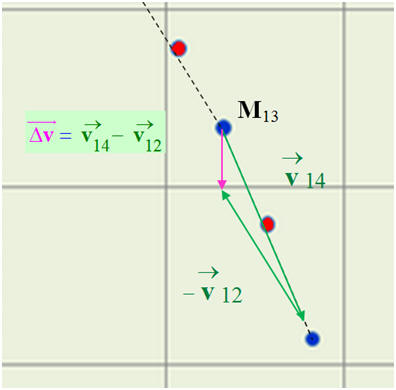
-    Valeur de l’accélération :

-      

-    Récapitulatif :

-     

 

b)-  comparer le représentant du vecteur  à celui donné au point 5 du document. (5 cm représente 1 m /s² )

-    Comparaison :

-    Théoriquement 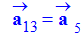  et on remarque que :

-     .

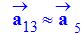-    expérimentalement :

-     

 

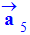-    Le vecteur est sensiblement égal au vecteur

3)- Accélération dans le repère de Frénet.

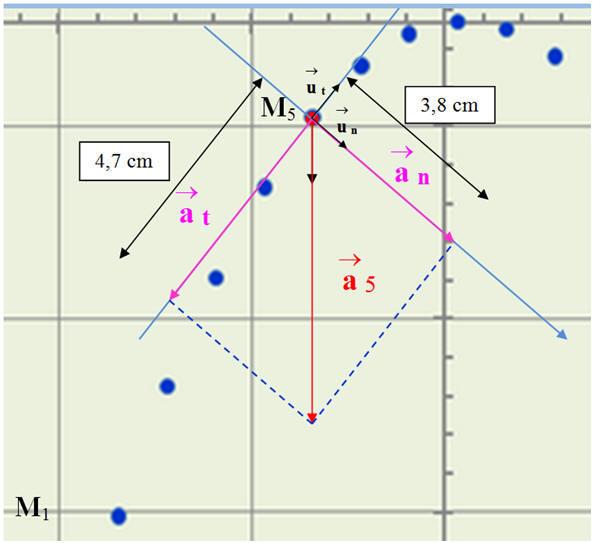
a)-  Déterminer la composante tangentielle du vecteur accélération au point 5.

-    composante tangentielle du vecteur accélération au point M₅.

-    Pour obtenir la composante tangentielle du vecteur accélération au point M₅ à partir de l’enregistrement, on projette le vecteur 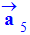sur la tangente à la parabole au point M₅.

-    Repère de Frenet :

 

 

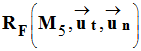
-    La longueur du représentant de la composante tangentielle mesure 4,7 cm.

-    On en déduit la valeur de l’accélération tangentielle :

-    .

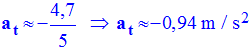-    Cette composante est négative car son sens est opposé à celui du mouvement (sens positif).

b)-  Justifier, à partir de l’enregistrement pourquoi elle n’est pas nulle ?

-    a_t ≠ 0, au cours du déplacement du mobile, la valeur de la vitesse varie au cours du temps.

-    On remarque que pendant la première phase la distance entre deux positions successives du mobile diminue alors que l'intervalle de temps reste égal à τ.

-    Le mouvement n’étant pas uniforme, il possède une accélération tangentielle.

-    L’accélération tangentielle traduit les variations de la valeur de la vitesse.

c)-  déterminer la composante normale du vecteur accélération au point 5.

-    composante normale du vecteur accélération au point 5.

-    Composante normale : on projette le vecteur accélération 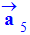 sur la perpendiculaire à la tangente à la parabole passant par le point M_5.

-    composante normale :

 

 

-    Longueur du représentant : ℓ = 3,8 cm : 

-     

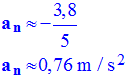
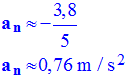
-    Vérification :

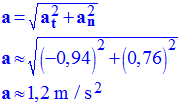
d)-  Justifier, à partir de l’enregistrement pourquoi elle n’est pas nulle ?

-    L’accélération normale n’est pas nulle car le vecteur vitesse change de direction à chaque instant.

-    Le mouvement n’est pas rectiligne.

-    L’accélération normale traduit les variations de la direction du vecteur vitesse au cours du mouvement.

e)-  Pouvez-vous expliquer, sans calcul, et de deux façons différentes, pourquoi l’accélération tangentielle est nulle au point O, sommet de la parabole.

-    l’accélération tangentielle est nulle au point O, sommet de la parabole.

-    Au sommet de la parabole, la vitesse est minimale :

-    .

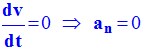-    Au sommet de la parabole, l'axe x'Ox est tangent à la parabole, en conséquence, a_x = a_t = 0.

4)- Testez vos connaissances sur l’accélération.

On considère les expressions suivantes où A₁, A₂ et A₃ peuvent être des vecteurs (préciser quand c’est le cas) ou des scalaires (nombres) :

                                             

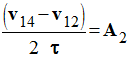
Répondre par Vrai ou Faux aux affirmations suivantes et justifier vos réponses.

            Expression A₁ :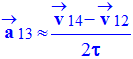

            Représente le vecteur accélération au temps t₁₃.                                  

            Expression A₂ :

            Représente la composante tangentielle du vecteur accélération au temps t₁₃.

            Expression A₃ :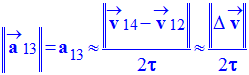

            Représente la norme, l'intensité ou la valeur de l'accélération au temps t₁₃.

a)-  A₁  traduit à la fois une variation de la direction et de la valeur de la vitesse.

-    VRAI. Expression A₁ :

-     

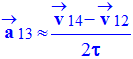
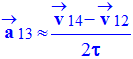
-    traduit à la fois les variations de la valeur de la vitesse et de la direction du vecteur vitesse.

-    Il traduit les variations du vecteur vitesse.

b)-  A₂  est la valeur du vecteur accélération.

-    FAUX. Expression A₂ :

-     

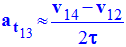
-    représente la composante tangentielle du vecteur accélération.

-    Elle traduit la variation de la valeur du vecteur vitesse.

c)-  A₂  traduit une variation de la valeur du vecteur vitesse.

-    VRAI. Expression A₂ :

-     

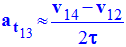
-    traduit la variation de la valeur, de l'intensité ou de la norme du vecteur  vitesse.

d)-  A₃  est la norme, la valeur ou l’intensité du vecteur accélération.

-    VRAI. Expression A₃ :

-     

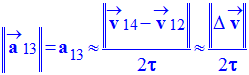
-    représente la norme, la valeur ou l'intensité du vecteur accélération.

e)-  A₃  est la composante tangentielle du vecteur accélération.

-    FAUX.

-     

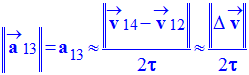
-    Ne pas confondre l’accélération tangentielle et l’accélération. (La composante tangentielle du vecteur accélération et le vecteur accélération)

5)- étude dynamique du mobile en mouvement sur le plan incliné.

a)-  Faire l’inventaire des forces qui s’exercent sur le mobile en mouvement.

-    Étude dynamique.

-    Bilan des forces : réaction du support , perpendiculaire au support car les frottements sont négligeables.

-    Poids du mobile .

b)-  déterminer, à partir des lois de Newton, les caractéristiques du vecteur accélération du centre d’inertie du mobile en mouvement sur le plan incliné.

-    Théorème du centre d'inertie :

-    Énoncé :

-    dans un référentiel galiléen, la somme des vecteurs forces extérieures appliquées au système est égale au produit de la masse m du système par le vecteur accélération de son centre d’inertie.

-     

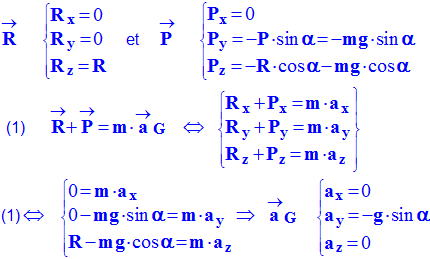
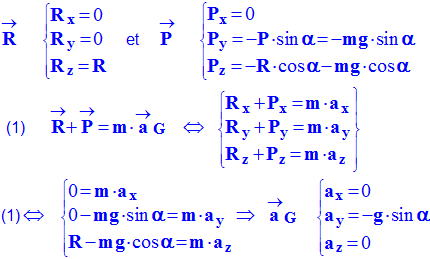
c)-  comparer ce résultat à celui obtenu dans la question 2)- a)-. Données : g = 9,8 m / s².

-    Valeur de l'accélération :

-     

 

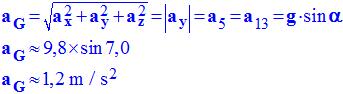
II-  Une base forte : l'ion éthanolate.

 

L'éthanol, de formule C₂H₅OH, réagit avec le sodium suivant l'équation bilan :

(Réaction 1)

L'ion éthanolate C₂H₅O ^–, formé au cours de cette réaction (1), réagit avec l'eau en donnant quantitativement de l'éthanol et des ions hydroxyde ; L’équation bilan de sa réaction avec l'eau est appelée réaction 2.

 

Protocole :

Dans un volume V₁ = 20,0 mL d'éthanol pur on introduit une masse m₂ = 1,00 g de sodium ; une réaction assez vive, exothermique se produit, accompagnée d'un dégagement gazeux important.

Après s'être assuré que tout le sodium a disparu, on refroidit le mélange réactionnel.

On verse dans une fiole jaugée de 200 mL contenant de l'eau distillée.

On complète jusqu'au trait de jauge avec de l'eau distillée. Soit S la solution homogène ainsi obtenue.

On dose une prise d'essai de volume V₀ = 10,0 mL de la solution S par une solution d'acide chlorhydrique de concentration C = 1,00 x 10 ^–1 mol / L.

 

Données : M (Na) = 23 g / mol ; M (H) = 1 g / mol ; M (C) = 12 g / mol ; M (O) = 16 g / mol

Masse volumique de l'éthanol : μ = 790 g / L.

1)- Étude des réactions 1 et 2.

a)-  Montrer que l'éthanol est introduit par excès par rapport au sodium.

-     

-    Quantité de matière d'éthanol :

-     

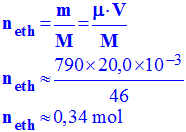
-     Quantité de matière de sodium :

-     

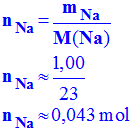
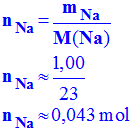
-    n_eth > n_Na : L'éthanol a été introduit en excès.

b)-  En déduire la quantité de matière n₃ d'ions éthanolate formée lors de la réaction 1.

-    Quantité de matière d'ions éthanolate formé. D'après le bilan molaire de la réaction (1) et sachant que l'éthanol a été introduit en excès, le sodium limite la réaction :

-     n₃ = n_Na ≈ 0,043 mol.

c)-  L'ion éthanolate est une base forte : Donner la définition d'une base forte. Écrire l'équation bilan de la réaction 2.

-    L'ion éthanolate est une base, elle capte un proton :

C₂H₅O^–   +   H⁺   =   C₂H₅OH

-    Réaction (2) :

C₂H₅O^–   +   H₂O   →   C₂H₅OH   +   HO^–

d)-  Quelles sont les caractéristiques de la réaction 2.

-    caractéristiques de la réaction 2 : Réaction totale, rapide, exothermique, unique.

2)- Dosage de la solution S.

a)-  Le volume de la solution d'acide chlorhydrique versé pour atteindre l'équivalence est V_eq = 21,4 mL. Par quelles méthodes peut-on repérer cette équivalence ?

-    Repérage de l’équivalence : dosage pH-métrique ou dosage colorimétrique.

b)-  Parmi les indicateurs colorés suivants, lequel choisir ? Justifier la réponse.

 

-    Indicateurs colorés : il faut choisir le B.B.T car le point d’équivalence appartient à la zone de virage.

-    À l’équivalence, le pH = 7 : Dosage acide fort base forte.

c)-  Définir l’équivalence.

-    Il y a équivalence lorsque les réactifs ont été mélangés dans les proportions stœchiométriques définies par les coefficients de la réaction.

 

d)-  Écrire l'équation bilan de la réaction support du dosage.

-    équation bilan de la réaction support du dosage.

H₃O⁺   +   HO^–    →     2 H₂O

e)-  Donner les caractéristiques de cette réaction.

-    caractéristiques de cette réaction : réaction totale, rapide, exothermique, unique

f)-    Donner la relation d’équivalence.

-    relation à l’équivalence :

-    n (HO^–) _initial = n (H3O⁺) _ajouté

g)-  Déduire du volume d'acide chlorhydrique versé à l'équivalence la quantité de matière, d'ions hydroxyde, présente dans les 200 mL de solution S.

-    quantité de matière, d'ions hydroxyde :

-    n (HO^–) _initial = C . V_eq

-    n (HO^–) _initial ≈ 1,00 x 10 ^{– 3}   x 21,4 x 10 ^{– 3}

-    n (HO^–) _initial ≈ 2,14 x 10 ^{– 3} mol / L

-    dans les 200 mL de solution S :

-     n (HO^–)  = n (HO^–) _initial  x 20 ≈ 2,14 x 10 ^{– 3}  x 20 mol / L

-    n (HO^–)  ≈ 0,0428 mol / L

h)-  Montrer que ce résultat est en accord avec la réponse donnée à la question 1)- b)-.

-    Ce résultat est en accord avec la réponse donnée à la question 1)- b)-. Car : du point de vue théorique :

-    Quantité de matière d'ions éthanolate formé. D'après le bilan molaire de la réaction (1) et sachant que l'éthanol a été introduit en excès, le sodium limite la réaction :

-     n₃ = n_Na ≈ 0,043 mol.

-    Or :

-    n (HO^–)  = n (CH₃COO^–)   ≈ 0,0428 mol / L

-    et expérimentalement, on trouve :

-    n (HO^–)  ≈ n (CH₃COO^–)

Fin