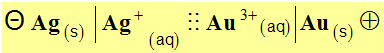On a réalisé 3 expériences avec le même mobile S de masse m.

Ce mobile est muni d’une soufflerie qui lui permet de se déplacer sur coussin d’air.

Le mobile est autoporteur lorsque la soufflerie est en marche et l’on peut négliger les forces de frottements.

Lorsque la soufflerie est à l’arrêt, le mobile n’est plus autoporteur et les frottements ne sont plus négligeables.

Les expériences 2 et 3 permettent de déterminer les valeurs des composantes tangentielle R_T et normale R_N dde la réaction du support.

1)- Le mobile S est suspendu à un dynamomètre par une ficelle de poids négligeable (voir l’expérience 1).

En appliquant les conditions d’équilibre et le principe de l’interaction, montrer que l’intensité de la force exercée par la ficelle sur le dynamomètre

est égale à l’intensité du poids du mobile S.

En déduire l’intensité P du poids du mobile S.

-  D’après le principe de l’interaction entre le fil et le mobile S,

-    (3)

-  D’après le principe de l’interaction entre le fil et le dynamomètre D ,

-  (4)

-  Les relations (1), (2), (3), (4) donnent :

-  P = F_fil/S = F_S/fil = F_fil/D = F_D/fil

-  valeur l’intensité P du poids du mobile S.

-  En conséquence :

-  P = F_fil/D ≈ 5,40 N

2)- Exploitation des expériences 2 et 3 :

a)-  A l’aide de l’expérience 2, déterminer la valeur de l’angle d’inclinaison α du support par rapport à l’horizontale.

-  La valeur de l’angle d’inclinaison α du support par rapport à l’horizontale.

-  Considérons comme système, le mobile S.

-  Il est en équilibre.

-  Il est soumis aux forces suivantes : Le poids, la tension du fil et la réaction du support

-  Les conditions d’équilibre :

-  S est soumis à des forces dont les effets se compensent et les forces sont concourantes et coplanaires.

-  Schéma :

-  La soufflerie étant en marche, les frottements sont négligeables :

-   

-  Coordonnées des différents vecteur dans le repère

-  La condition nécessaire d’équilibre permet d’écrire :

-   

b)-  A l’aide de l’expérience 3, déterminer les valeurs de R_T et de R_N.

-  valeurs de R_T et de R_N.

-  Les frottements ne sont plus négligés, le mobile S est à l’arrêt, c’est-à-dire en équilibre.

-  Le solide S est soumis à son poids  et à la réaction du support , force que l’on peut décomposer :

-  Schéma :

             ou       

-  La condition nécessaire d’équilibre permet d’écrire :

-   

La soufflerie étant arrêtée (voir expérience 3), on augmente progressivement l’inclinaison du support.

Le coefficient de frottement  est pratiquement constant et μ = 0,60.

c)-  Montrer qu’il existe une valeur α₀ de l’angle α et un sens du vecteur vitesse pour lesquels le mobile est en translation rectiligne uniforme.

-  valeur α₀ de l’angle α pour lequel le mobile est en translation rectiligne uniforme.

-  Le mobile est en translation rectiligne uniforme.

-  En conséquence le centre d’inertie du solide S est animé d’un mouvement rectiligne uniforme :.

-  D’après la réciproque du principe de l’inertie :

-   

d)- L’angle α est supérieur à α₀ . On abandonne le mobile sans vitesse initiale. Décrire qualitativement son mouvement.

-  L’angle α est supérieur à α₀ .

-  Le mobile n’est plus pseudo-isolé, il est animé d ‘un mouvement rectiligne accéléré.

Cliquer sur l'image pour l'agrandir

1)- Calculer, en m/s, les valeurs des vitesses instantanées aux points A₁, A₆ et A₁₀.

-  valeurs des vitesses instantanées aux points A₁, A₆ et A₁₀.

-   

2)- Tracer les vecteurs vitesses en ces points. Expliquer la méthode utilisée.

 Échelle : 1 m/s ↔ 4 cm

-  Tracé des vecteurs vitesses en ces points : méthode utilisée.

-  La direction du vecteur vitesse : tangente à la trajectoire au point considéré (parallèle issue de A₁ à la droite (A₀A₂).

-  Le sens : celui du mouvement et la longueur, celui du représentant.

Cliquer sur l'image pour l'agrandir

-   

3)- Que peut-on en déduire pour le mouvement de la bille ?

-  mouvement de la bille.

-  Le vecteur vitesse change de direction et de valeur à chaque instant.

-  Le mouvement du centre d’inertie de la bille est curviligne varié.

-  La trajectoire est un arc de parabole.

4)- On considère le système formé par la bille. Faire le bilan des forces appliquées à la bille.

Donner les caractéristiques de chaque force. Le système est-il pseudo-isolé ? Justifier la réponse.

-  bilan des forces appliquées à la bille. caractéristiques de chaque force.

-  On néglige la résistance de l’air car dans le titre, on parle de chute libre. La bille est soumise à l’action du poids.

-  Le poids (force à distance) :

-  Direction : verticale du lieu

-  Sens : vers le bas

-  Point d’application : centre d’inertie G

-  Valeur : P = m.g

-  le système n’est pas pseudo isolé car

5)- Que peut-on déduire à propos du vecteur vitesse du centre d’inertie du système ?

Ce résultat est-il en accord avec les résultats des questions 2)- et 3)- ?

-  Le système n’étant pas pseudo isolé, , d’après le principe de l’inertie,

le vecteur vitesse du centre d’inertie n’est pas un vecteur constant  ce qui correspond aux résultats du 2 et 3 :

-   

Pour déboucher les canalisations, on utilise des produits domestiques qui sont des solutions concentrées

d’hydroxyde de sodium (lessive de soude) contenant quelques adjuvants que l’on néglige.

On se propose de préparer une solution diluée à l’aide de l’une d’entre elles.

► Matériel mis à disposition :

-  Pipettes jaugées de 5 mL, 10 mL, 20 mL.

-  Pipette graduée de 10 mL.

-  Pipeteur ou propipette.

-  Fioles jaugées de 50 mL, 100 mL, 200 mL, 250 mL, 500 mL.

-  Béchers gradués de 50 mL, 100 mL, 250 mL.

-  Éprouvettes graduées de 10 mL, 50 mL, 100 mL, 250 mL.

-  Gants et lunettes de protection.

► Produits disponibles :

-  Eau distillée

-  Produit déboucheur 1,00 L

► Données :

-  Masse molaire de l’hydroxyde de sodium : M(NaOH) = 40,0 g.mol^-1.

-  Masse volumique de l’eau : μ₀ = 1,00 kg / dm³

2)-  Concentration de la solution commerciale :

a)-  Calculer la masse m’ de un litre de solution commerciale.

-  masse de un litre de solution commerciale.

-  m’ = μ . V = μ₀ . d .V ≈ 1,00 x 1,21 x 1,00

-  m’ ≈ 1,21 kg  

b)-  Calculer la masse m, d’hydroxyde de sodium, contenue dans un litre de solution commerciale.

-  masse d’hydroxyde de sodium, contenue dans un litre de solution commerciale.

-   

c)-  En déduire la quantité de matière n, d’hydroxyde de sodium, contenue dans un litre de solution commerciale.

-  quantité de matière n, d’hydroxyde de sodium, contenue dans un litre de solution commerciale.

-    

d)-  Montrer que la concentration molaire volumique de la solution commerciale S₁ a pour valeur C₁ = 6,05 mol / L.

En déduire le titre massique t_m de la solution.

3)- On veut diluer la solution commerciale pour obtenir un volume V₂ = 200 mL de solution S₂ de concentration .

-  Faire des schémas légendés représentant les différentes étapes de la préparation de la solution S₂.

-  Indiquer aussi les précautions à prendre pour la réalisation de la dilution.

-    Justifier l’utilisation de chaque matériel ou produit.

-  schémas légendés représentant les différentes étapes de la préparation de la solution S₂.

-  On verse environ 20 mL de solution commerciale dans un bécher de 150 mL.

-  On pipette avec une pipette jaugée (2 traits) de 5 mL.

-  On verse les 5 mL de solution commerciale dans une fiole jaugée de 200 mL contenant un peu d’eau distillée.

-  On ajoute de l’eau distillée environ aux ¾, on mélange,

-    puis on complète avecde l’eau distillée jusqu’au trait de jaugée.

-    On homogénéise en fin d'opération.

-  précautions à prendre pour réaliser la dilution. Justification du choix du matériel ou produit.

-  La solution étant très concentrée, il faut utiliser des lunettes et des gants.

-  La réaction entre l’hydroxyde de sodium et l’eau étant très exothermique,

-    il faut verser un peu d’eau distillée dans la fiole jaugée avant d’introduire la solution commerciale.

-    Il faut verser doucement la solution commerciale.

-  Choix du matériel : une fiole jaugée de 200 mL (dans l’énoncé, il est demandé de préparer 200 mL de solution diluée)

-  Un bécher de 150 mL (on ne pipette jamais dans la solution mère, il faut verser la solution mère dans un bécher).

-  Une pipette jaugée de 5 mL :

-  au cours de la dilution, il y a conservation de la quantité de matière de soluté :

4)- Écrire l’équation bilan de la réaction de dissolution de l’hydroxyde de sodium dans l’eau.

-  En déduire la concentration des ions présents dans la solution S₂.

-  équation bilan de la réaction de dissolution de l’hydroxyde de sodium dans l’eau.

-  En déduire la concentration des ions présents dans la solution S₂.

-  D’après l’équation de la réaction (1) :

-   

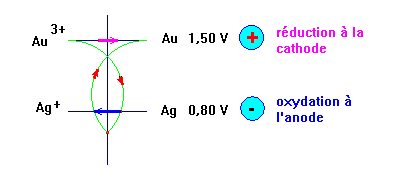
On réalise une pile en associant les deux demi-piles faisant intervenir les couples oxydant / réducteur suivants :

Au ³⁺ / Au et Ag ⁺ / Ag

1)- Dessiner cette pile, indiquer la polarité des électrodes et déterminer sa f.é.m. Donner son schéma conventionnel.

-  Dessin de la pile, polarité des électrodes, f.é.m. et schéma conventionnel.

-   électrode d’or : borne + et électrode d’argent : borne –.

-   La force électromotrice :

-  e _Ag–Au = E⁰ _{(Au3+ / Au)} –  E⁰ _{(Ag+ / Ag)}

-  e _Ag–Au ≈ 1,50 – 0,80

-  e _Ag–Au ≈ 0,70 V

-  Schéma conventionnel :

2)- nommer chaque électrode, donner les réactions aux électrodes et indiquer s'il s'agit d'une réduction ou d'une oxydation.

-  à la cathode se produit une réduction :

 Au³⁺  +  3 e^–  →    Au 

-  à l'anode se produit une oxydation :

Ag      →    Ag⁺  +  e^–

3)- Écrire l'équation bilan de la réaction qui s'effectue lorsque la pile débite du courant.

4)- On laisse la pile fonctionner pendant Δt = 3 h. On constate que la masse de l'électrode d'or a varié de m = 98 mg.

-  Au cours de la réaction, de l'argent disparaît, la masse de l'électrode d'argent diminue.

-  D'après de bilan des quantités de matière de l'équation bilan de la réaction :

-  Calcul de x :

-  La masse de l'électrode d'or a varié (augmentée) de m = 98 mg

-   

5)- La masse de l'électrode d'argent a-t-elle augmenté ou diminué ?  Justifier.

 Calculer la variation de masse m' de l'électrode d'argent.

-  La quantité de matière d’argent a diminuée de 3 x.

-  m’ = 3 x . M (Ag)

-  m’ ≈ 3 × 5,0 × 10 ^{– 3} × 107

-  m’ ≈ 0,16 g

6)- Calculer l'intensité supposée constante I du courant qui a circulé.

-  D'après le bilan de quantités de matière de la demi-équation électronique du couple Au³⁺ / Au

-  Quantité de matière d’électrons consommés : n (e^–) = 3 x

-