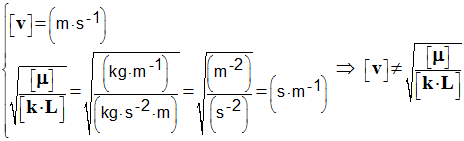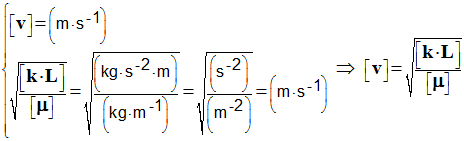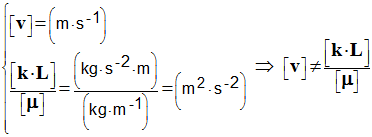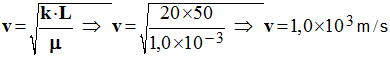|
Correction |
|
|
EXERCICE III : LE TELEPHONE "POT DE YAOURT" (4 points)
A l'ère du téléphone portable, il est encore possible de communiquer
avec un système bien plus archaïque…
|
L'onde sonore produite par le premier interlocuteur fait vibrer le fond du pot de yaourt, le mouvement de va et vient de celui-ci, imperceptible à l'œil, crée une perturbation qui se propage le long du fil. Cette perturbation fait vibrer le fond du second pot de yaourt et l'énergie véhiculée par le fil peut être ainsi restituée
sous la forme d'une onde
sonore perceptible par un second protagoniste. |
Données:
célérité du son dans l'air à
A- A PROPOS DES ONDES
|
1)- Identifier la chaîne des différents milieux de propagation des ondes mécaniques au sein du dispositif : - de la bouche de la personne qui
parle, à l'oreille de la personne qui écoute (figure1). - L'onde sonore se propage d'abord dans l'air, puis fait vibrer le fond du 1er pot de yaourt qui se comporte comme la membrane d’un H.P,
- ensuite le signal se propage dans
le fil, puis dans le
fond du 2nd pot de yaourt
et finalement dans l'air
pour arriver à l’oreille du second
protagoniste. |
|
Ce fil légèrement élastique peut être modélisé par un ressort à spires
non jointives. Les schémas suivants illustrent les conséquences de deux modes de déformation d'un ressort : l'écartement d'une extrémité du ressort selon une direction perpendiculaire à l'axe de celui-ci produit une onde de cisaillement (figure 2),
alors qu'une déformation selon l'axe du ressort produit une onde de
compression (figure 3). |
|
2)-
Attribuer, à chacune des situations représentées sur les
figures 2 et
3, les termes d'onde
longitudinale et d'onde transversale. Justifier votre réponse. - Onde longitudinale (figures 3) : - la direction de déplacement temporaire de la matière et la direction de propagation de l'onde sont les mêmes. - On parle aussi d'ondes de compression : - elles créent de proche en proche des ondes de compression -détente du milieu de propagation. - Elles vibrent parallèlement à leur direction de propagation (cas du ressort) - Onde transversale (figures 2) : - la direction de déplacement temporaire de la matière et la direction de propagation de l'onde sont perpendiculaires. - On parle aussi d'ondes de cisaillement. - Elles vibrent perpendiculairement à leur direction de propagation (cas de la corde) |
Seul le second mode de déformation
(figure 3) correspond au
phénomène observé sur le fil du dispositif étudié par la suite.
B- CELERITE DE L'ONDE QUI SE PROPAGE LE LONG DU FIL
|
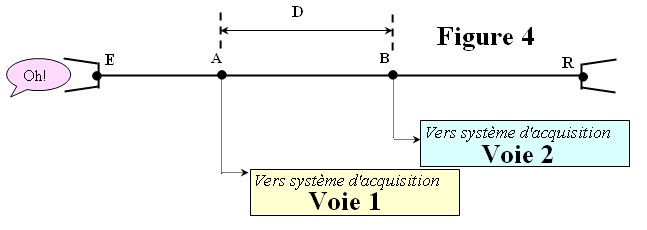
A
Deux capteurs, reliés en deux points
A et
B distants de
D =
détectent
successivement le passage d’une perturbation générée par un son bref à
l’entrée du pot de yaourt émetteur
E. |
Les capteurs enregistrent l'amplitude de cette perturbation au cours du
temps.
|
1)- A partir de l'enregistrement (figure 5), déterminer avec quel retard τ,
par rapport au point A,
le point B est atteint
par le signal. |
|
|
|
Figure 5
Sensibilité verticale :
1 mV / div
pour les deux
voies
Sensibilité horizontale :
5 ms / div |
|
|
|
- Retard entre le point B et le point A : - τ = x . s - τ = 4 × 5
-
τ =
20
ms
2)- Donner l'expression de la célérité v de l'onde sur ce fil en fonction de D et τ. Calculer sa valeur.
Comparer cette valeur à celle de la
célérité du son dans l'air à
Quelle propriété justifie ce résultat ? - Célérité v de l'onde sur ce fil en fonction de D et τ.
- - Propriété de l’onde : - Remarque : - La célérité de l'onde le long de la corde est supérieure à celle dans l'air. - La célérité d’une onde dépend du milieu de propagation. - Une onde sonore se déplace plus vite dans un solide que dans l’air. - La célérité de l’onde est une propriété du milieu de propagation.
Le fil
ER
de longueur
L
=
Dans le cas d'un fil, le produit
k.L
est une constante caractéristique du milieu de propagation.
3)-
Un modèle simple de la célérité
v d'une onde de ce type
dans ce fil correspond à l'une des expressions suivantes:
(1)
- Retrouver la bonne expression parmi celle proposées en effectuant
une analyse dimensionnelle.
- Expression (1) :
- L’expression (1) est à rejeter, elle n’est pas homogène à une vitesse.
- Expression (2) :
- L’expression (2) est à retenir, elle est homogène à une vitesse.
- Expression (3) :
- L’expression (3) est à rejeter, elle n’est pas homogène à une vitesse.
4)-
Calculer la célérité de l'onde sur le fil
ER.
- Ce résultat est en accord avec celui obtenu précédemment. |
|
Une autre méthode, permettant de déterminer la célérité v de l'onde se propageant dans le fil, consiste à placer, devant le pot de yaourt émetteur, un haut parleur (figure 6) qui émet des ondes sonores sinusoïdales de fréquence fE.
Les ondes sinusoïdales qui se propagent dans le fil ont la même
fréquence. |
|
Lorsque la distance D est
égale à
on obtient
l'enregistrement de la figure 7. |
|
|
|
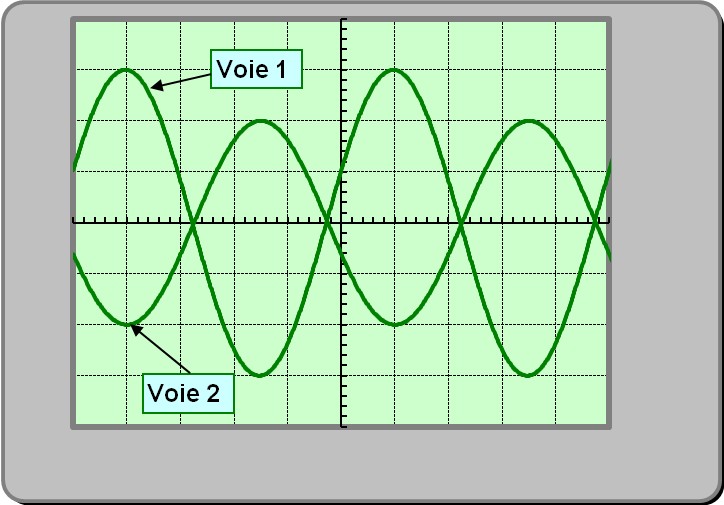
Figure 7
Sensibilité verticale :
1 mV / div
pour les deux voies
Sensibilité horizontale :
1 ms / div |
|
5)-
Comment peut-on expliquer que l'amplitude du signal au point
B (voie 2) soit plus faible
que l'amplitude du signal au point
A (voie 1) ? - Le point B est plus éloigné de la source que le point A. - Au cours de la propagation, l’onde s’amortie à cause des frottements. - L’énergie transportée par l’onde diminue au cours de la propagation.
6)-
A partir de l'enregistrement de la
figure 7, déterminer la
fréquence f de l'onde qui se
propage dans le fil. - Fréquence f de l'onde qui se propage dans le fil - À l’aide de l’oscillogramme, on peut déterminer la valeur de la période du signal : - T = x . s - T = 5 × 1 - T = 5 ms - On peut en déduire la valeur de la fréquence :
-
7)-
Lorsque l'on éloigne le point B,
du point A, on constate que
les signaux se retrouvent dans la même configuration pour les valeurs de
la distance:
D
=
a) En déduire la valeur de la longueur d'onde
l
associée à l'onde qui se propage dans le fil, puis la célérité
v de cette onde.
- Pour la distance
D =
- Cette distance est égale à un nombre entier de fois la longueur d’onde : - On peut écrire que : k . λ = 25,0 (1) avec k entier naturel.
- Pour la distance
D =
- On peut écrire que : (k + 1) . λ = 30,0 (2) - Et enfin : (k + 2) . λ = 35,0 (3)
- Des relations (1), (2) et (3), on tire :
λ =
b) Sur la figure de l'annexe à rendre avec la copie, représenter
l'allure de la courbe que l'on observerait sur la voie 2 si la distance
D était égale à |
Schéma :
|
|
Sensibilité verticale : 1 mV / div pour les deux voies
Sensibilité
horizontale :
1 ms / div |
|
8)- La voix est un signal complexe constitué d'ondes sonores de fréquences différentes. A l'écoute des signaux transmis, le fil ne semble pas être un milieu de propagation notablement dispersif. Qu'est-ce qu'un milieu dispersif ?
Quelle serait la conséquence sur les signaux reçus si
le fil qui constitue le dispositif était un milieu de propagation très
dispersif ? - Un milieu est dispersif si la célérité de l’onde dans le milieu dépend de la fréquence imposée par la source. - Si le fil était un milieu dispersif, les ondes de basses fréquences ne se propageraient pas à la même célérité que les ondes de hautes fréquences. - Il y aurait un décalage entre les sons de différentes fréquences. - Le téléphone pot de yaourt ne fonctionnerait pas.
L'antenne d'un téléphone portable, émet ou reçoit des ondes
électromagnétiques qui ont les mêmes propriétés que la lumière.
9)-
Quelle différence fondamentale existe-t-il concernant la propagation des
ondes du téléphone "pot de yaourt" et celles d'un téléphone portable ? - Les ondes électromagnétiques peuvent se propager dans le vide contrairement aux ondes mécaniques qui nécessitent la présence d’un milieu matériel pour se propager.
|
Annexe :




 (2)
(2) (3)
(3)