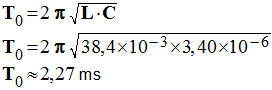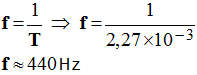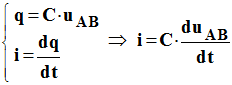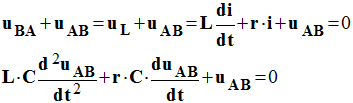|
|
Exercice 2 : Le Xylophone électronique 4 points
|
On réalise un montage série comprenant un condensateur d’armatures A et B, de capacité C = 3,40 μF, initialement chargé, une bobine d’inductance
L = 38,4 mH et de
résistance r =
9,0 Ω et
d’un interrupteur
K ouvert. On utilise un dispositif informatisé d’acquisition de données qui permet de visualiser sur la voie 1 la tension uAB aux bornes du condensateur en fonction du temps. Au temps
t = 0 s, on ferme
l’interrupteur K et
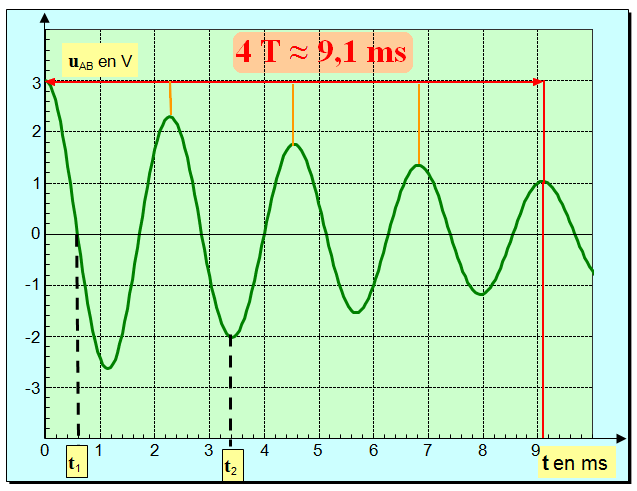
simultanément, on réalise l’acquisition. On obtient l’enregistrement suivant : |
Cliquer sur l'image pour l'agrandir
|
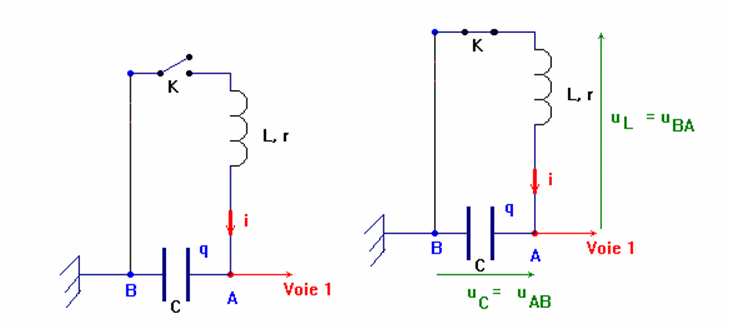
1)- Faire un schéma légendé du circuit. Représenter la tension aux bornes du condensateur et la tension aux bornes de la bobine.
-
Schéma du
circuit :
Cliquer sur l'image pour l'agrandir 2)- Quel est le phénomène physique mis en évidence ? - Phénomène physique mis en évidence :
-
décharge oscillante du condensateur dans la bobine. 3)- Mesurer la pseudo-période T des oscillations électriques. Comparer cette valeur à la période propre T0 du circuit (L, C) idéal et conclure.
Cliquer sur l'image pour l'agrandir - Pseudo-période des oscillations : - 4 T ≈ 9,1 ms
-
T
≈
2,27 ms
-
- T
≈ T0
- L’amortissement est faible. 4)- Les oscillations électriques sont transformées à l’aide d’un amplificateur et d’un haut-parleur en un son audible de même fréquence. a)- à une fréquence donnée correspond une hauteur musicale identifiée par une note :
-
Quelle
est la hauteur musicale du son produit ?
- Hauteur musicale
du son produit :
-
- C’est le
La3 b)- Par quel facteur faut-il multiplier ou diviser la valeur de la capacité C du condensateur pour obtenir la note La4 de fréquence f = 880 Hz ? - Pour ce faire, il faut multiplier la valeur de la fréquence par deux, c’est-à-dire diviser la période par 2.
- En conséquence, diviser la valeur de la capacité par
4.
5)- équation différentielle : a)- établir la relation liant l’intensité du courant i dans le circuit, la tension uAB aux bornes du condensateur et sa capacité C.
- Avec l’orientation
choisie pour le circuit :
- b)- établir l’équation différentielle que vérifie la tension uAB aux bornes du condensateur. Justifier.
- En utilisant
l’additivité des tensions, on peut écrire :
-
6)- Charge et énergie électromagnétique : a)- Calculer la valeur de la charge portée par l’armature A du condensateur au temps t = 0 s.
- Valeur de la
charge portée par l’armature A du condensateur au temps
t
= 0 s
- q = C . uAB
=> q
(0) =
3,40
× 10–3 × 3,0
- q
(0) =
1,0
×
10–5 C b)- Dans quel dipôle est stockée l’énergie électromagnétique E1 de l’oscillateur au temps t1 ? Justifier. - Au temps t1, la tension aux bornes du condensateur est nulle. - L’énergie emmagasinée dans le condensateur est nulle. - Au cours des oscillations, des échanges d’énergie se produisent entre le condensateur et la bobine.
- L’énergie se trouve emmagasinée dans la bobine au temps
t1. c)- Dans quel dipôle est stockée l’énergie électromagnétique E2 de l’oscillateur au temps t2 ? Justifier. - Au temps t2, la tension aux bornes du condensateur est extrémale. - L’énergie est emmagasinée dans le condensateur.
- Le condensateur est
chargé et l’intensité dans le circuit est nulle. La bobine ne
possède
pas d’énergie. d)- Calculer la valeur de la charge portée par l’armature A du condensateur au temps t2. Conclure.
- Valeur de la
charge portée par l’armature A du condensateur au temps
t2 - q = C . uAB
- q
(t2) =
3,40
× 10–3
× (– 2,0)
- q
(t2)
= –
6,8
× 10–6
C
- La charge portée
par l’armature A est négative au temps t2.
- De plus la valeur
absolue de la charge diminue au cours du temps. |