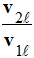|
Métropole 2011 : Bac Sciences Physiques Exercice 2 : CHUTE VERTICALE D'UN BOULET
(5,5 points) Énoncé et Correction |
|
|
|
Exercice
2 : CHUTE VERTICALE D’UN BOULET (5,5 points) |
Exercice 2 : CHUTE VERTICALE D’UN BOULET (5,5 points)
|
Selon la légende, Galilée (1564-1642) aurait étudié la chute des corps en lâchant divers objets du sommet de la tour de Pise (Italie). Il y fait référence dans deux ouvrages : Dialogue sur les deux grands systèmes du monde et Discours concernant deux sciences nouvelles dans lesquels il remet notamment en question les idées d'Aristote. Dans cet exercice, on présente trois
courts extraits de ces deux livres. Il s’agit de retrouver certains résultats avancés par Galilée concernant la chute verticale dans l’air d’un boulet sphérique en fer, lâché sans vitesse initiale. Pour cette étude, on choisit le référentiel terrestre, supposé galiléen, auquel on adjoint un repère d’espace (Ox) vertical orienté vers le bas (Photo 1). |
Photo 1
La Tour de Pise |
Donnée :
![]() Intensité du champ de pesanteur, supposé
uniforme : g = 9,8 m . s –2
Intensité du champ de pesanteur, supposé
uniforme : g = 9,8 m . s –2
|
1. Modélisation par une chute libre. 1.1. Étude des hauteurs de chute. |
|
Extrait n° 1 : « Avant tout, il faut considérer que le mouvement des corps lourds n’est pas uniforme : partant du repos, ils accélèrent continuellement (…). Si on définit des temps égaux quelconques, aussi nombreux qu’on veut, et si on suppose que, dans le premier temps, le mobile, partant du repos, a parcouru tel espace, par exemple une aune*, pendant le second temps, il en parcourra trois, puis cinq pendant le troisième (…) et ainsi de suite, selon la suite des nombres impairs ». * une aune = 1,14 m Le boulet est lâché au point O, d’abscisse x0 = 0 à la date t0 = 0. On suppose l’action de l’air négligeable ; dans ce cas,
l’équation horaire du mouvement du centre d’inertie
G du boulet
est :
|
|
1.1.1. Soient x1 la distance parcourue au bout de la durée τ, x2 la distance parcourue au bout de la durée 2 τ et
ainsi de suite, exprimer
x1,
x2,
x3
en fonction de
g et de
τ. 1.1.2.
Exprimer la différence
h1
= x1 –
x0
en fonction
de g et de
τ puis
les différences
h2
= x2 –
x1
et h3
= x3 –
x2 en fonction
de h1. 1.1.3.
Retrouve-t-on la suite des hauteurs de chute annoncée par Galilée dans
l’extrait n°1 ? Justifier. 1.2. Étude de la durée de la chute Les points de vue d’Aristote et de Galilée, au sujet de l’influence de la masse m du boulet sur la durée totale Δt de sa chute, diffèrent. |
|
Extrait n° 2 : « Cherchons à savoir combien de temps
un boulet, de fer par exemple, met pour arriver sur Aristote dit qu’une « boule de fer de cent livres**, tombant de cent coudées, touche terre avant qu’une boule d’une livre ait parcouru une seule coudée », et je vous dis, moi, qu’elles arrivent en même temps. Des expériences répétées montrent qu’un boulet de cent livres met cinq secondes pour descendre de cent coudées ». * une coudée correspond à une distance de 57 cm ; ** une livre est une unité de masse |
|
1.2.1. Parmi les propositions ci-dessous, attribuer celle qui correspond à la théorie d’Aristote et celle qui correspond à la théorie de Galilée : a) La durée de chute augmente quand la masse du boulet augmente ; b) La durée de chute diminue quand la masse du boulet augmente ; c) La durée de chute est indépendante de la masse. 1.2.2.
En utilisant l'expression
Ce résultat est différent de la valeur annoncée dans l’extrait n° 2. Proposer une explication à l’écart constaté. |
|
Galilée admet plus loin que les deux boules, de masses respectives une et cent livres, arrivent au sol avec un léger écart. |
|
Extrait n° 3 : « Vous constatez, en faisant l’expérience, que la plus grande précède la plus petite de deux doigts, c’est à dire que quand celle-là frappe le sol, celle-ci s’en trouve encore à deux doigts. Or, derrière ces deux doigts, vous ne retrouverez pas les quatre-vingt-dix-neuf coudées d’Aristote. » |
|
On considère que trois forces s’exercent sur un boulet pendant sa chute verticale : Son poids
La norme de la force de frottement a pour
expression :
Où v est la vitesse du centre d’inertie du boulet, R est le rayon du boulet et C est une constante sans unité. Données :
2.1. Lors de la chute, représenter ces trois forces sur un schéma sans souci d’échelle. 2.2. Le poids et la poussée d’Archimède sont constants pendant la chute d’un boulet. Établir le rapport de leurs expressions et en déduire que la poussée d’Archimède est négligeable. 2.3. Étude dynamique 2.3.1. Appliquer la deuxième loi de Newton. Projeter les forces sur l’axe (Ox) vertical orienté vers le bas (Photo 1). Déterminer l’expression de la dérivée par rapport au temps de la
vitesse
2.3.2.
En déduire que l’expression de la vitesse
limite v
ℓ
est :
2.3.3. Vérifier, en effectuant une analyse dimensionnelle, que l'expression de vℓ est bien homogène à une vitesse. 2.4. On considère deux boulets sphériques B1 et B2 en fer de masses respectives m1 = 1 livre et m2 = 100 livres et de rayons respectifs R1
= On note v 1ℓ et v 2ℓ les vitesses limites respectives des boulets B1 et B2. Exprimer le rapport
2.5. Un logiciel permet de simuler les évolutions de la vitesse v (t) (figure 2) et de la position x (t) du boulet pendant sa chute (figure 3 et zoom de la figure 3 sur la figure 4). Ces courbes sont obtenues pour les trois situations suivantes : - La chute du boulet B1 dans l’air (courbes c et c’), - La chute du boulet B2 dans l’air (courbes b et b’), - La chute libre (courbes a et a’). 2.5.1. Expliquer l’attribution des courbes b et c aux boulets B1 et B2. 2.5.2.
La hauteur de chute est de
2.5.3. À quelle distance du sol se trouve l’autre boulet à cette date ? Ce résultat est-il en accord avec l’extrait n° 3 ? |
|
|
|
|