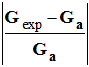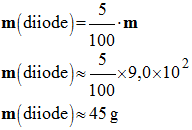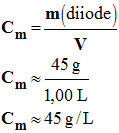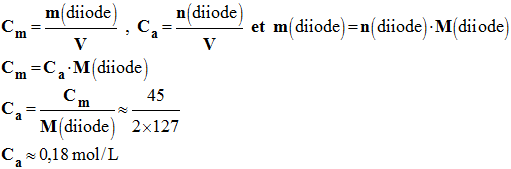Exercice 2 : Spectrophotométrie (5,5 pts)

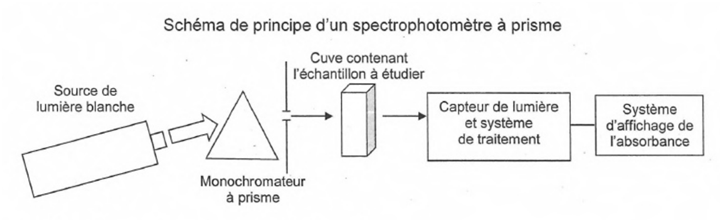
La lumière est un « outil » précieux en chimie analytique. En effet, toute espèce chimique est susceptible d’interagir avec des radiations lumineuses. Par exemple, une espèce colorée X absorbe certaines radiations visibles. Le principe de la spectrophotométrie repose sur la mesure de l’absorbance A de l’espèce X en solution dans un solvant Y. Cette grandeur A est le résultat de la comparaison de deux intensités lumineuses : celle d’une radiation monochromatique ayant traversé une cuve transparente contenant le solvant Y, et celle de la même radiation émergeant de la même cuve contenant la solution de l’espèce X dans le solvant Y.

 

 

1. 1^ière partie : lumière et spectrophotométrie.

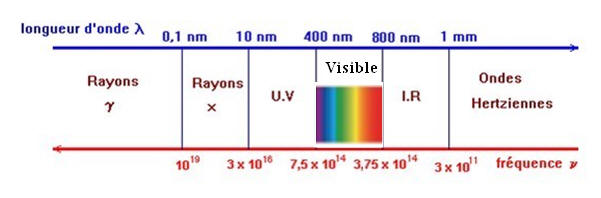
1.1. Donner les valeurs limites des longueurs d’onde du spectre visible dans le vide et les couleurs correspondantes. -   Valeurs limites des longueurs d’onde du spectre visible dans le vide et les couleurs correspondantes : -   L’œil humain n’est sensible qu’aux radiations dont les longueurs d’onde sont comprises entre 400 nm et 800 nm. Cliquer sur l'image pour l'agrandir 1.2. Situer, du point de vue de leur longueur d’onde, les rayonnements ultraviolets et infrarouges par rapport au spectre visible. Cliquer sur l'image pour l'agrandir -   I.R : 800 nm ≤ λ ≤ 1 mm -   U.V : 10 nm ≤ λ ≤ 400 mm 1.3. Le rôle du monochromateur dans un spectrophotomètre est de sélectionner une radiation monochromatique particulière. Donner la définition d’une lumière monochromatique. -  Lumière monochromatique : -  Une lumière monochromatique ne contient qu’une seule radiation et ne peut être décomposée par un prisme. -  C’est une radiation lumineuse qui est caractérisée par sa longueur d’onde λ0 (lambda) (en mètre m) dans le vide ou l’air ou sa fréquence ν (en hertz Hz). 1.4. Certains monochromateurs comportent un prisme de verre. 1.4.1. Définir l’indice de réfraction n d’un milieu transparent. -   Indice de réfraction n d’un milieu transparent : -   Pour une radiation donnée, un milieu transparent homogène est caractérisé par un indice de réfraction n. -   Relation :   n : indice de réfraction c : vitesse de la lumière dans le vide en m / s v : vitesse de la lumière dans le milieu transparent en m / s -   Remarque : comme c ≥ v alors n ≥ 1 1.4.2. De quel paramètre caractéristique d’une radiation lumineuse dépend l’indice n pour un milieu transparent donné ? -   Paramètre caractéristique d’une radiation lumineuse dont dépend l’indice n pour un milieu transparent donné : -   L’indice de réfraction n d’un milieu transparent dépend de la longueur fréquence ν (en hertz Hz) de la radiation qui le traverse. 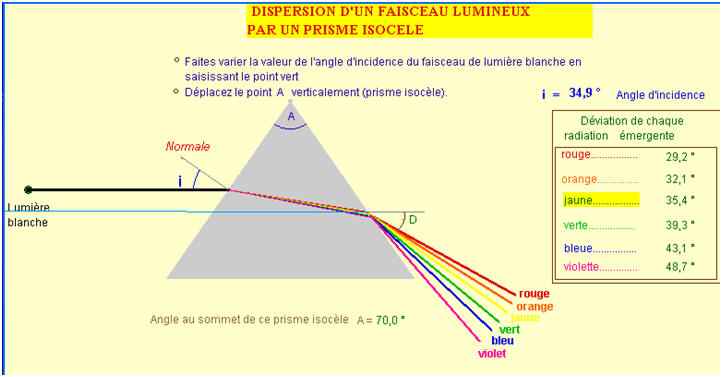-   Ou : -   L’indice de réfraction n d’un milieu transparent dépend de la longueur d’onde dans le vide λ0 de la radiation qui le traverse. 1.4.3. Le prisme de verre décompose la lumière blanche. Nommer le phénomène responsable de cette décomposition et le décrire brièvement en quelques lignes. -   Phénomène responsable de cette décomposition : -   Le prisme dévie et décompose la lumière blanche en lumières colorées du rouge au violet. -   C'est un phénomène de dispersion. -   L'ensemble des couleurs obtenues constitue le spectre de la lumière blanche. -   Le spectre est continu du rouge au violet. -   Lorsqu’une lumière arrive sur un prisme, elle subit deux réfractions : -   Une sur la face d’entrée et une sur la face de sortie. -   Deuxième loi de la réfraction : n1 . sin i1 = n2 . sin i2  -   Le trajet d’une radiation dépend de l’indice du prisme car l’angle d’incidence est le même pour les différentes radiations qui constituent la lumière blanche. -   Le trajet d’une lumière dans le prisme dépend de sa couleur. -   Or ce trajet dépend de l’indice du prisme. 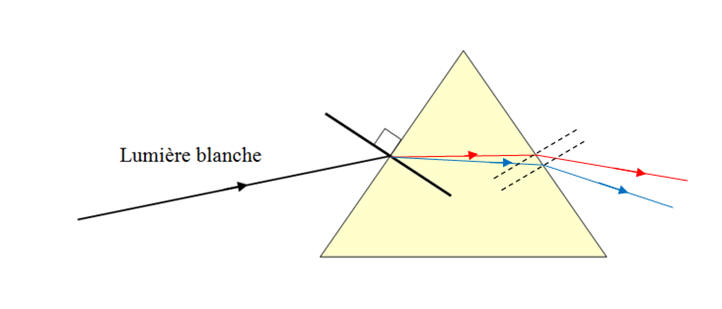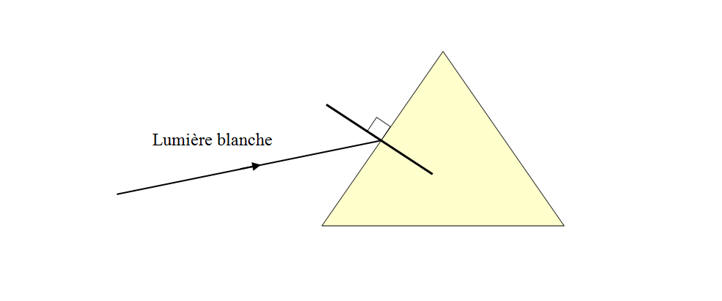-   C’est le phénomène de dispersion. 1.4.4. Lors d’une réfraction air-verre, la déviation d’une radiation lumineuse est d’autant plus importante que la longueur d’onde de la radiation est faible. Sans faire de calcul, compléter la figure de la feuille annexe (à rendre avec la copie) en y faisant figurer le trajet d’un rayon lumineux bleu et d’un rayon rouge à l’intérieur du prisme et après sa sortie. -  On indique que : « la déviation d’une radiation lumineuse est d’autant plus importante que la longueur d’onde de la radiation est faible… » : -  Comme λbleue < λrouge, la radiation bleue est plus déviée que la radiation rouge. Cliquer sur l'image pour l'agrandir Cliquer sur l'image pour l'agrandir

2. 2^ième partie : Dosage colorimétrique par étalonnage.

On se propose de déterminer la concentration en diiode dans une teinture d’iode officinale. On commence par diluer 200 fois la teinture d’iode (trop concentrée pour une étude spectrophotométrique directe). La solution aqueuse obtenue à l’issue de cette dilution est appelée solution S. Par ailleurs, on dispose d’un ensemble de solutions aqueuses de diiode notées Di (D1, D2, etc.) de concentrations connues toutes différentes. Ces solutions ont des colorations proches de celle de la solution S.

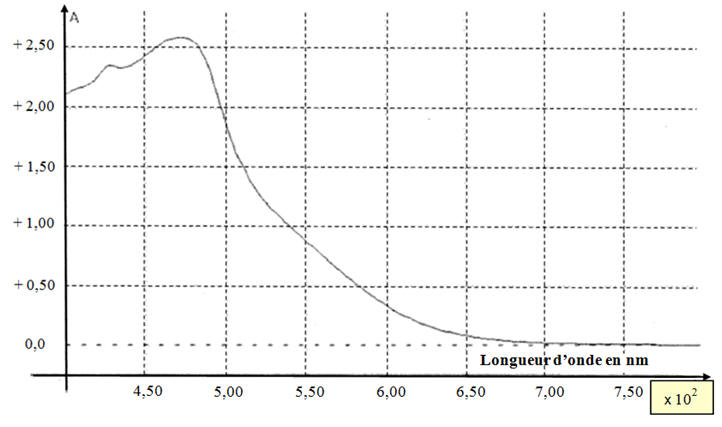
Données :

Spectre d’absorption d’une solution aqueuse de diiode

de concentration molaire C = 3,0 x 10 ^{– 3} mol.L^–1

 

Cliquer sur l'image pour l'agrandir

Masse molaire atomique de l’iode : 127 g.mol^-1

 

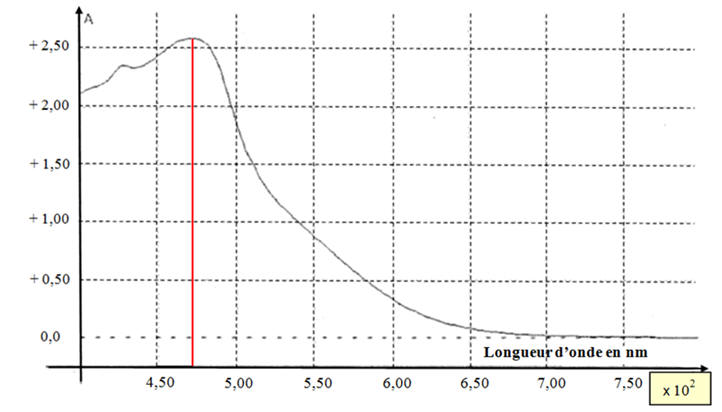
Écart relatif entre une valeur expérimentale Gexp et une valeur attendue Ga d’une grandeur quelconque G : 2.1. On peut trouver expérimentalement un encadrement de la concentration en diiode de la solution S, sans utiliser un spectrophotomètre. 2.1.1.  Expliquer brièvement la méthode. -   Pour trouver expérimentalement un encadrement de la concentration en diiode de la solution S, on réalise une échelle des teintes. -   À partir d’une solution mère, on prépare des solutions filles par dilutions successives que l’on place dans des tubes à essais identiques. -   On connait ainsi la concentration des différentes solutions filles que l’on dispose dans l’ordre. -   On verse la solution S dans un tube à essais et on compare la teinte de cette solution à celle des solutions filles. 2.1.2.  Pourquoi lors de la mise en œuvre de cette méthode, faut-il que les récipients utilisés (tubes à essais ou béchers) soient tous identiques ? -   Il faut que les récipients utilisés (tubes à essais ou béchers) soient tous identiques car la teinte d’une solution dépend de l’épaisseur de solution traversée. 2.2. À l’aide d’un spectrophotomètre, on mesure l’absorbance Ai de chaque solution Di de diiode, puis celle de la solution S. 2.2.1. Donner la valeur d’une longueur d’onde qui vous paraît bien appropriée pour ces mesures. Justifier brièvement. Cliquer sur l'image pour l'agrandir Longueur d’onde 200 nm 23 nm mesures 8,4 0,98 -   Longueur d’onde maximale : λmax ≈ 450 + 23 -    λmax ≈ 473 nm -   On choisit λmax = 473 nm, pour avoir le maximum de variations pour la valeur de l’absorbance A. -   Cette longueur d’onde λmax correspond au maximum d’absorption. 2.2.2.  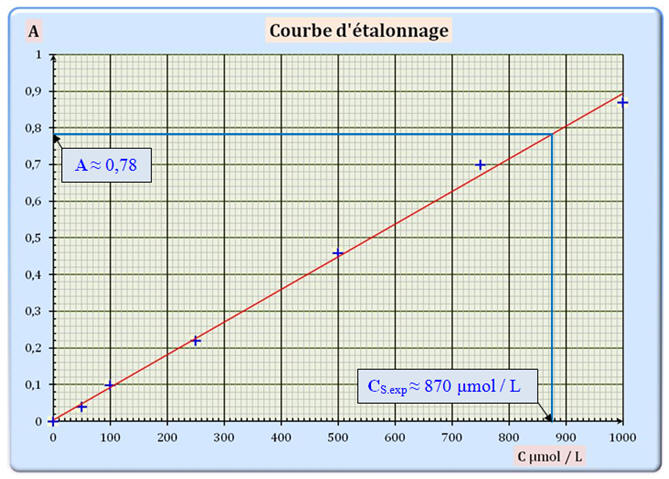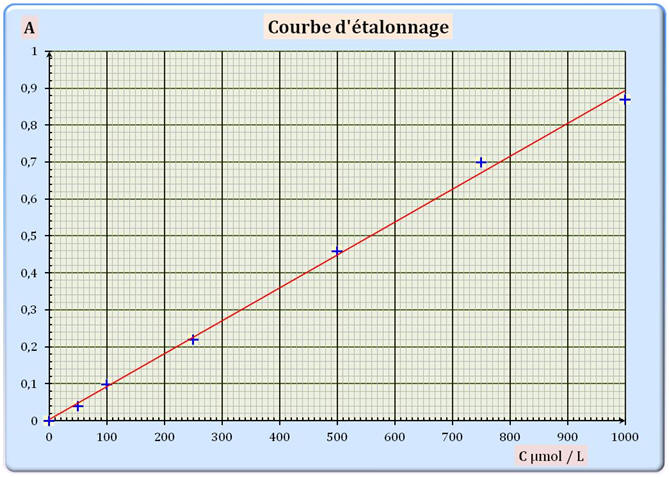On obtient les résultats suivants : Concentration C de la solution en μmol / L 50 100 250 500 750 1000 Absorbance A de la solution 0,041 0,10 0,22 0,46 0,70 0,87 Absorbance de la solution S : A = 0,78. La courbe d’étalonnage de l’absorbance en fonction de la concentration molaire C en diiode est fournie en annexe. La relation entre l’absorbance A et la concentration C est appelée loi de Beer-Lambert. Elle s’écrit : A = k . C avec k une constante et C la concentration molaire de l’espèce colorée dans la solution. La courbe d’étalonnage obtenue est-elle en accord avec cette loi ? Justifier. -  Les points sont sensiblement alignés. -  La courbe obtenue est un segment de droite passant par l’origine. -  On en déduit que pour les concentrations utilisées, -  l’absorbance A est proportionnelle à la concentration C en diiode de la solution. : -  En conséquence : A = k . C -  Ceci est bien en accord avec la loi de Beer-Lambert. 2.2.3. Déterminer graphiquement la concentration molaire CS.exp en diiode de la solution S. En déduire la concentration molaire Cexp en diiode de la teinture d’iode officinale. - Concentration molaire CS.exp en diiode de la solution S : Cliquer sur l'image pour l'agrandir -  La lecture graphique donne pour A = 0,78, -  CS.exp ≈ 870 μmol / L. -  On indique dans le texte : « On commence par diluer 200 fois la teinture d’iode (trop concentrée pour une étude spectrophotométrique directe). » -  La solution en diiode de de la teinture d’iode officinale a été diluée 200 fois : -  Cexp = 200 CS.exp -  Cexp ≈ 200 x 870 -  Cexp ≈ 0,174 mol / L 2.3. La teinture d’iode officinale est étiquetée à 5,0 % en masse de diiode. Sa masse volumique est ρ = 9,0 x 102 g . L– 1. 2.3.1.  À partir de ces données, vérifier que la concentration massique Cm en diiode attendue dans cette teinture est 45 g . L– 1. -  Concentration (ou titre) massique Cm en diiode : -  On donne la masse volumique de la teinture d’iode officinale : -  ρ = 9,0 x 102 g . L–1 -  Masse de 1,00 L de solution : -  m = ρ . V -  m ≈ 9,0 x 102 x 1,00 -  m ≈ 9,0 x 102  g -  La teinture d’iode officinale est étiquetée à 5,0 % en masse de diiode : -    -  En conséquence, dans 1,00 L de teinture d’iode officinale, il y a 45 g de diiode : -    -  C’est bien la valeur attendue. 2.3.2.  En déduire la valeur de la concentration molaire attendue en diiode dans cette teinture. On la notera Ca. -  Valeur de la concentration molaire attendue en diiode dans cette teinture : -     2.3.3.  Calculer l’écart relatif entre la valeur expérimentale Cexp à la valeur Ca. Conclure. -  Écart relatif entre la valeur expérimentale Cexp à la valeur Ca : -   -  La valeur expérimentale est proche de la valeur attendue. -  L’écart relatif est d’environ 3,3 %.

 

Questions 2.2.2 et 2.2.3 : Courbe d’étalonnage :