![]()
|
|
|
|
|
|
|
|
Exercices : DS
|
|
QCM r
|
1)- Exercice : Exploitation d’une courbe de résonance.
|
Exploitation d’une courbe de résonance Le graphique représente la courbe de réponse d’un système
oscillant soumis à des oscillations forcées. 1.
Déterminer la valeur de la fréquence de
résonance. 2.
Déterminer la valeur de la largeur de la
bande passante à 3 dB. |
|
Exploitation d’une courbe de résonance : 1.
Valeur de la fréquence de résonance.
-
L’amplitude des oscillations
du système oscillant (résonateur) dépend de la fréquence f de
l’excitateur.
-
Cette amplitude est maximale
lorsque
f0 =
fR.
-
C’est-à-dire lorsque la
fréquence de l’excitateur est égale à la fréquence du résonateur.
-
On dit que le résonateur
entre en résonance. - Le résonateur est caractérisé par sa courbe de réponse donnant l’amplitude des oscillations
en fonction de la fréquence délivrée par l’excitateur :
xm =
f (f).
-
À la résonance, l’amplitude
xm
des oscillations est maximale.
-
Détermination graphique :
-
fR
≈ 25 Hz.
-
xmR
≈ 2,0 cm. 2.
Valeur de la largeur de la bande passante à
3 dB.
-
Pour un amortissement
important, le phénomène de résonance disparaît pratiquement.
-
L’acuité de la résonance
dépend de l’amortissement.
-
Plus l’amortissement est
faible et plus la résonance est aiguë et inversement.
-
Acuité de la résonance.
-
Un résonateur est
caractérisé par sa bande passante à 3 décibels (3 dB). - La bande passante à 3 dB est l’ensemble des fréquences pour lesquelles l’amplitude xm est supérieure à l’amplitude à la résonance divisée par
-
En conséquence :
-
Δf
= f2 –
f1 représente la
bande passante à 3 dB. :
-
Dans le cas présent :
-
xmR ≈ 2,0 cm et
-
Exploitation graphique :
-
Δf =
f2 –
f1
-
Δf
≈ 33 – 16
-
Δf
≈ 17 Hz
-
On peut en déduire la valeur du
facteur de qualité Q du
résonateur :
-
On définit aussi le facteur de
qualité pour un résonateur :
-
|
2)- Tracé d’une courbe de réponse :
|
Tracé d’une courbe de réponse : Au cours d’une séance de travaux pratiques, on a relevé les valeurs xm des amplitudes d’un résonateur en
fonction de la fréquence f de l’excitateur.
1.
Tracer la courbe représentative de
l’amplitude xm en fonction de la fréquence f. 2.
Déterminer la fréquence fR
de résonance et la valeur (xm)R
correspondante. 3.
Déterminer graphiquement les valeurs de f2
et f1 des fréquences correspondantes à une
amplitude :
-
|
|
Tracé d’une courbe de réponse : 1.
Courbe représentative de l’amplitude xm
en fonction de la fréquence f.
-
Réalisé avec le tableur Excel : 2.
Fréquence fR de résonance
et la valeur (xm)R correspondante.
-
Tableau de mesures :
-
Fréquence de résonance :
-
L’amplitude des oscillations
du système oscillant (résonateur) dépend de la fréquence f de
l’excitateur.
-
Cette amplitude est maximale
lorsque
f0 =
fR.
-
C’est-à-dire lorsque la
fréquence de l’excitateur est égale à la fréquence du résonateur.
-
On dit que le résonateur
entre en résonance.
-
Exploitation graphique : 3.
Valeurs de f2 et f1
des fréquences correspondantes :
-
Acuité de la résonance.
-
Un résonateur est
caractérisé par sa bande passante à 3 décibels (3 dB). - La bande passante à 3 dB est l’ensemble des fréquences pour lesquelles l’amplitude xm est supérieure à
l’amplitude à la résonance divisée par
-
En conséquence :
-
Δf
= f2 –
f1 représente la
bande passante à 3 dB. :
-
Dans le cas présent :
-
xmR ≈ 27,2 cm et
-
Exploitation graphique :
-
En conséquence :
-
f1 ≈ 18 Hz et
f2 ≈ 24,3 Hz
-
On peut calculer la valeur de bande à
3 dB :
-
Δf =
f2 –
f1
-
Δf
≈ 24,3 – 18
-
Δf
≈ 6,3 Hz
-
On peut en déduire la valeur du
facteur de qualité Q du
résonateur :
-
On définit aussi le facteur de
qualité pour un résonateur :
-
|
|
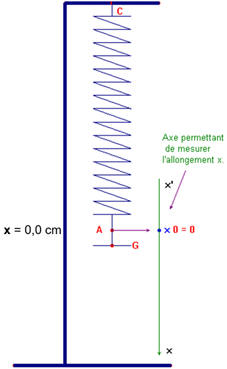
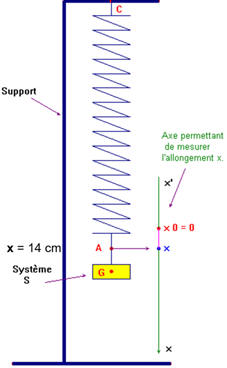
Oscillateur élastique : On considère le dispositif schématisé sur le document ci-dessous. Le solide S a une masse m = 216 g. Le ressort est à spires non jointives ; Sa constante de raideur est k et sa masse est négligeable.
-
Tableau de valeurs :
1. Préalablement à l’expérience, on accroche une masse marquée de 200 g à l’extrémité libre du ressort suspendu à un support. On mesure un allongement Δℓ = 14,0 cm. Déterminer
la valeur de la constante de raideur k du ressort. Donnée :
g = 9,8 N . kg–1. 2. Le ressort étant suspendu à un support, on accroche à son extrémité des masses marquées telles que la masse totale soit égale à 216 g. On écarte de système de sa position d’équilibre et on l’abandonne sans vitesse initiale. La durée de 10
oscillations, mesurée avec un chronomètre donne une moyenne égale à
7,82 s. a.
Quel type d’oscillations observe-t-on ? b.
Vérifier que le résultat de la mesure est en
accord avec l’expérience précédente. 3. On utilise le dispositif ci-dessous. On note dans un tableau la fréquence n de l’excentrique et
l’amplitude xm des oscillations du solide sur le
banc à coussin d’air.
-
Tableau de valeurs :
a.
Quel type d’oscillations observe-t-on ?
Préciser le résonateur et l’excitateur. b.
Représenter sur une feuille de papier
millimétré, le graphique donnant l’amplitude xm
des oscillations en fonction de la fréquence f de
l’excitateur. c.
Quel phénomène ce graphique met-il en
évidence ? Évaluer la fréquence de résonance fR. 4.
Déterminer : a.
Les bornes de la bande passante à 3dB. b.
La largeur de la bande passante Δf. c.
Le facteur de qualité
d.
Comparer fR et f0,
fréquence propre du résonateur. Conclure.
|
Oscillateur élastique : 1.
Déterminer la valeur de la constante de
raideur k du ressort.
-
Donnée : g = 9,8 N . kg–1.
-
Masse marquée
m = 200 g
-
Allongement : Δℓ = Δx =
14,0 cm.
-
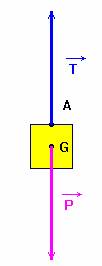
Schémas :
Tension
d'un ressort. Équilibre d'un solide.
-
Le
référentiel d’étude est le support. C’est un référentiel terrestre.
-
Le
système S (c’est-à-dire la masse marquée)
-
Est
soumis à l’action exercée par
-
L’action exercée par
-
Est
soumis à l’action du ressort (action de contact).
-
L’action exercée par le ressort sur le système S est appelée,
tension du ressort :
-
Principe de l’Inertie :
-
Énoncé : tout corps persévère dans son état de repos ou de mouvement
rectiligne uniforme si les forces qui s’exercent sur
lui se compensent.
-
Condition d’équilibre :
-
Caractéristiques du vecteur Poids :
-
Point d’application : G
-
Direction : verticale du lieu passant par G : la
droite (AG)
-
Sens : du haut vers le bas : de A vers G.
-
Valeur : P = m . g
-
Caractéristiques du vecteur tension d’un ressort :
-
Point d’application : le point d’attache A
-
Direction : la droite (AG)
-
Sens : du bas vers le haut : de G vers A.
-
Valeur : T = P = m . g
(1)
-
Schéma à l’équilibre :
-
Constante de raideur du ressort :
-
Le ressort étant à spires non
jointives, il y a proportionnalité entre la tension
T exercée par le ressort
et l’allongement : - Δℓ = Δx.
-
T =
k . Δℓ
(2)
-
Or T = P = m .
g (1)
-
En combinant (1) et (2) :
-
2.
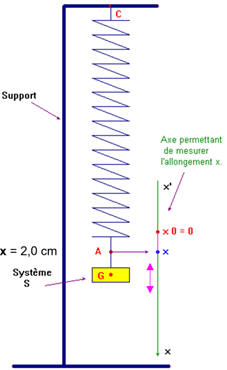
Premier type d’oscillations.
-
Schéma du dispositif :
-
Le système
S oscille autour de sa
position d’équilibre.
-
Expression de la période propre du
pendule élastique (masses marquées + ressort) :
-
-
Analyse dimensionnelle.
-
-
Masses marquées
m’ = 216 g.
-
On écarte de système de sa position
d’équilibre
-
On l’abandonne sans vitesse initiale.
-
Durée de 10 oscillations : Δt
= 7,82 s a.
Type d’oscillations :
-
On observe des oscillations libres
peu amorties. b.
Vérification du résultat.
-
On peut calculer la période propre
des oscillations de façon théorique et comparer
le résultat obtenu avec la valeur
expérimentale :
-
-
Valeur expérimentale :
-
-
T ≈
T0
-
Le résultat est en accord avec
l’expérience. 3.
Deuxième type d’oscillations .
-
Tableau de valeurs :
n
(tr , min–1)
f
(Hz)
xm
(cm)
24
0,40
1,0
36
0,60
1,3
48
0,80
1,6
60
1,00
2,3
66
1,10
3,5
72
1,20
7,3
74
1,24
12,1
77
1,28
13,4
79
1,32
11,9
82
1,36
6,0
84
1,40
4,8
90
1,50
3,0
96
1,60
1,7
108
1,80
1,0
120
2,00
0,6
132
2,20
0,4 a.
Type d’oscillations :
-
On observe des oscillations forcées.
-
Résonateur : le pendule élastique
constitue le résonateur.
-
L’excitateur : le moteur avec son
excentrique constitue l’excitateur. b.
Graphique donnant l’amplitude xm
= g (f).
-
Graphe : c.
Phénomène graphique mis en évidence :
-
Phénomène de résonance d’amplitude :
-
L’amplitude des oscillations
du système oscillant (résonateur) dépend de la fréquence f de
l’excitateur.
-
Cette amplitude est maximale
lorsque
f0 =
fR.
-
C’est-à-dire lorsque la
fréquence de l’excitateur est égale à la fréquence du résonateur.
-
On dit que le résonateur
entre en résonance.
-
Le résonateur est
caractérisé par sa courbe de réponse donnant l’amplitude des
oscillations
en fonction de la
fréquence délivrée par l’excitateur : xm =
f (f).
-
À la résonance, l’amplitude
xm
des oscillations est maximale.
-
Fréquence de résonance
fR :
-
À la résonance l’amplitude des
oscillations du résonateur est maximale.
-
Exploitation graphique :
-
fR ≈ 1,28 Hz
-
fR ≈ 1,3 Hz
-
Amplitude à la résonance :
xmR
≈ 13,4 cm 4.
Détermination : a.
Les bornes de la bande passante à 3dB.
-
Acuité de la résonance.
-
Un résonateur est
caractérisé par sa bande passante à 3 décibels (3 dB).
-
La bande passante à 3 dB est
l’ensemble des fréquences pour lesquelles l’amplitude xm est supérieure à
l’amplitude à la résonance divisée par
-
En conséquence :
-
Δf
= f2 –
f1 représente la
bande passante à 3 dB. :
-
Dans le cas présent :
-
xmR ≈ 13,4 cm
-
-
Exploitation graphique :
-
En conséquence :
-
f1
≈ 1,21 Hz et f2 ≈ 1,34 Hz b.
La largeur de la bande passante Δf.
-
On peut calculer la valeur de bande à
3 dB :
-
Δf =
f2 –
f1
-
Δf
≈ 1,34 – 1,21
-
Δf
≈ 0,13 Hz c.
Le facteur de qualité
-
On peut en déduire la valeur du
facteur de qualité Q du
résonateur :
-
On définit aussi le facteur de
qualité pour un résonateur :
-
-
On remarque que :
-
Si
Q ≈ 10, la
résonance est aiguë.
-
On peut détériorer le système. d.
Comparaison de fR et f0,
fréquence propre du résonateur.
-
-
D’autre part, la fréquence de
résonance :
-
fR ≈ 1,28 Hz
-
Conclusion :
fR ≈ f0
-
Il y a résonance lorsque la fréquence
de l’excitateur (fR)
est égale de la fréquence propre du résonateur (f0).
![]() .
.![]()
![]()
![]()
![]()



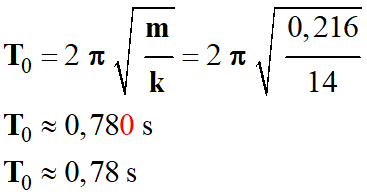
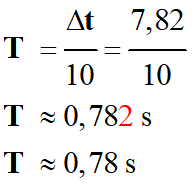
 .
.![]()

![]() .
.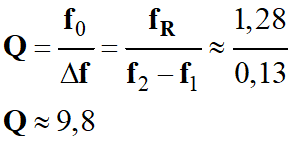

![]()
4)- Résonance d’une corde de piano :
|
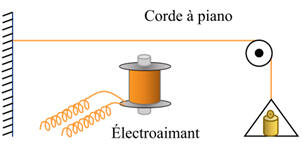
Résonance d’une corde de piano : On tend une corde de piano au-dessus d’un électroaimant. La tension de la corde est importante de l’ordre de 400 N. La bobine de l’électroaimant est parcourue par un courant
alternatif de fréquence f.
1.
: a.
Pourquoi les pôles de l’électroaimant
sont-ils alternativement nord et sud ? b.
Avec quelle fréquence un pôle
d’électroaimant retrouve-t-il le même nom ? 2. L’acier est attiré aussi bien par un pôle nord que par un pôle sud de l’électroaimant. Choisir parmi les propositions
suivantes, la valeur de la fréquence f’ avec laquelle la
corde est attirée : f / 2 : f :
2 f. 3. La corde constitue un oscillateur élastique en régime forcé. Elle vibre avec la fréquence f’. L’amplitude des vibrations est
importante pour certaines vibrations particulières vérifiant la
relation :
-
f’ =
p ×
f1 (p : nombre
entier)
-
Donnée :
f1 = 128 Hz a.
Pour quelles fréquences f de l’intensité du
courant qui traverse l’électroaimant, la corde va-t-elle vibrer
fortement ? b.
Comment appelle-t-on se phénomène ? |
Résonance d’une corde de piano : 1.
: a.
Pôles de l’électroaimant alternativement
nord et sud :
-
Le courant étant alternatif,
l’intensité du courant change de sens de façon périodique.
-
Comme le sens du champ magnétique
b.
Fréquence à laquelle un pôle d’électroaimant
retrouve le même nom :
-
Les pôles de l’aimant changent de nom
à la fréquence f du
courant alternatif. 2.
Fréquence f’ avec laquelle la corde
est attirée :
-
f / 2 :
f : 2 f.
-
La corde est attirée quel que soit le
nom du pôle de l’aimant.
-
La corde vibre à la fréquence 2
f car l’électroaimant
attire la corde aussi bien quand le pôle de l’électroaimant est un
pôle nord ou sud. 3.
: a.
Fréquences f de l’intensité du
courant pour lesquelles la corde vibre fortement :
-
f’ =
p ×
f1 (p : nombre
entier)
-
Donnée :
f1 = 128 Hz
-
L’amplitude des oscillations est
importante pour f1
= 128 Hz.
-
En conséquence la fréquence de la
tension excitatrice :
-
-
La corde vibre fortement pour les
fréquences :
-
f =
p ×
fu (p : nombre
entier)
-
f = 64 ×
p b.
Nom du phénomène :
-
La corde constitue le résonateur et
l’électroaimant l’excitateur.
-
On est en présence d’un phénomène de
résonance
-
Pour
p = 1 , la fréquence de
la tension excitatrice est f = 64 Hz, on observe 1 fuseau :
-
Pour
p = 2 , la fréquence de
la tension excitatrice est f = 128 Hz, on observe 2 fuseaux.
-
Pour p = 3 , la fréquence de
la tension excitatrice est f = 192 Hz, on observe 3 fuseaux
-
La corde de piano constitue un
résonateur à fréquences multiples.
![]() dépend du sens du courant, la
nature des pôles de l’aimant dépendent du sens du courant.
dépend du sens du courant, la
nature des pôles de l’aimant dépendent du sens du courant.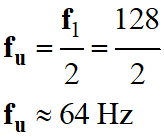
![]()
![]()
![]()
![]()
|
|