![]()
|
|
|
|
|
|
|
|
QCM r
|
1)- Exercice 09: Comparaisons entre les forces de gravitation et les forces électriques :
|
Comparaisons entre les forces de gravitation et les forces
électriques : La molécule de diazote est constituée de deux atomes d’azote dont
les noyaux comportent 7 protons. Les noyaux sont à la distance d = 0,14 nm l’un de l’autre. Donnée : La masse de chaque noyau est m = 2,3 × 10–26
kg. 1. Déterminer la valeur des forces d’interaction électrique entre les deux noyaux. Ces forces
sont-elles attractives ou répulsives ? 2. Déterminer la valeur des forces d’interaction gravitationnelle entre les deux noyaux. Ces forces
sont-elles attractives ou répulsives ? 3.
Comparer les valeurs de ces deux forces
d’interaction. Conclure. |
|
Comparaisons entre les forces de gravitation et les forces
électriques : 1.
Valeur des forces d’interaction électrique
entre les deux noyaux. - Dans le vide, deux particules A et B, portant les charges électriques respectives qA et qB, séparées par la distance d sont
soumises à deux forces directement opposées :
-
-
Expression :
-
-
Dans le cas présent :
qA = qB
= 7 e > 0
-
-
k :
constante
-
-
Charge élémentaire : e = 1,60
× 10–19 C
-
Schéma :
-
Valeur de la force d’interaction
électrique :
-
-
Les charges étant de même signe, les
forces sont répulsives. 2.
Valeur des forces d’interaction
gravitationnelle entre les deux noyaux. - Deux corps ponctuels A et B de masses respectives mA et mB exercent l’un sur l’autre des forces d’attraction, directement opposées, dirigées suivant la droite (AB), de valeur proportionnelle aux masses et inversement proportionnelle
au carré de leur distance d.
-
-
Dans le cas présent :
-
-
Application numérique :
-
-
Les forces d’attraction
gravitationnelle sont toujours attractives. 3.
Comparaison des valeurs de ces deux forces
d’interaction.
-
Étude du rapport :
-
-
Conclusion :
-
À l’échelle du noyau, la force de
gravitation est très faible devant la force électrique.
►
Analogies : les forces électriques et
les forces de gravitation, sont :
-
Proportionnelles aux grandeurs qui
les créent
-
Et inversement proportionnelle au
carré de la distance.
►
Différences :
-
Les forces de gravitation sont
toujours attractives alors que les forces électriques sont
attractives ou répulsives.
-
À l’échelle macroscopique les forces
électriques sont négligeables devant les forces de gravitation,
-
À l’échelle microscopique les forces
de gravitation sont négligeables par rapport aux forces électriques.
►
Attention :
-
Pour la valeur de la force : les
charges sont des grandeurs algébriques.
-
Pour ne pas avoir de problème :
-
il
faut écrire
-
|
2)- Exercice 13 : Le condensateur plan :
|
Le condensateur plan : La d.d.p entre deux plaques conductrices planes, parallèles est
distantes de d = 2,0 cm est : VP – VN = 600
V 1.
Faire un schéma représentant les lignes de
champ. 2.
Quelle relation donne la valeur du champ
électrique entre les deux plaques ? Préciser l’unité. 3.
Représenter le champ en un point M
situé entre les plaques. Échelle : 1 cm ↔ 10 kV . m–1. |
|
Particule chargée dans un champ électrique : 1.
Schéma représentant les lignes de champ.
-
Autre représentation :
-
-
Un champ électrique est dit uniforme
dans une région de l’espace si le vecteur champ
conserve en tout point de
cette région, la même direction, le même sens et la même valeur.
-
Les lignes de champ sont des droites
parallèles entre elles.
-
Une ligne de champ vectoriel est une
ligne tangente en chacun de ses points au vecteur champ.
-
Elle est orientée par une flèche dans
le même sens que celui du champ. 2.
Relation donnant la valeur du champ
électrique entre les deux plaques
-
Caractéristiques du champ électrique
-
Relation :
-
Valeur du champ :
-
E : Valeur du champ électrique
-
Unité
: ( V . m–1)
-
3.
Représentation du champ en un point M
situé entre les plaques.
-
Échelle : 1 cm ↔ 10 kV . m–1.
-
E ≈ 30 kV . m–1
-
Longueur du représentant du vecteur
champ électrique
-
ℓ ≈ 3,0 cm
-
Schéma :
|
||||||||||||||||
3)- Exercice 17 : Particule chargée dans un champ électrique :
|
Particule chargée dans un champ électrique Une particule chargée est située dans un
champ électrique
E = 5,0 × 105 V . m–1, Elle est soumise à une force électrique de sens opposé au vecteur
Fe = 8,0 × 10-14 N. 1.
: a.
Donner l’expression de la force électrique. b.
Représenter le champ et la force électrique. 2.
: a.
Calculer la valeur de la charge électrique. b.
Quel est le signe de la charge électrique ? |
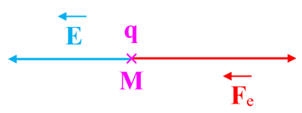
Particule chargée dans un champ électrique
-
Valeur du champ électrique :
-
E = 5,0 × 105 V . m–1
-
Force électrique :
-
Fe = 8,0 × 10-14
N 1.
: a.
Expression de la force électrique.
-
On note q la charge de la
particule chargée :
-
La force électrostatique
-
Relation donnant la valeur de la
force électrique Fe :
-
Fe = |q| .
E b.
Représentation du champ et de la force
électrique
-
Schéma :
-
Échelle : Échelle : 1 cm ↔ 2,0 × 10-14
N 2.
: a.
Valeur de la charge électrique.
-
Fe = |q| .
E
-
b.
Signe de la charge électrique :
-
La charge électrique
q est négative car les vecteur champ électrique
-
q = – e = – 1,6 × 10–19
C
![]()
![]()
![]()
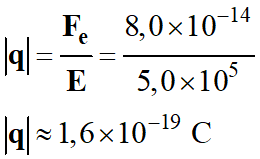
![]() et force électrique
et force électrique ![]() ont des sens opposés :
ont des sens opposés :![]()
4)- Exercice 20 : Pendule chargé dans un champ électrique :
|
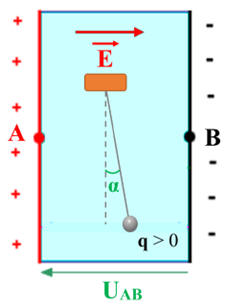
Pendule chargé dans un champ électrique : Un pendule électrique, de charge q, est placé dans un
champ électrique
Il s’écarte d’un angle de 10 ° par rapport à sa position
d’équilibre verticale. 1.
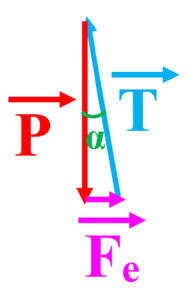
Faire un schéma en précisant le signe de la
charge q. 2.
La masse m de la boule du pendule est
égale à m = 0,10 g a.
Faire le bilan des forces s’exerçant sur la
boule. b.
Énoncer la loi d’équilibre d’un solide
soumis à trois forces. c.
Calculer la force électrique s’exerçant sur
la boule. d.
En déduire la valeur de la charge q.
-
Donnée : g = 10 m . s–2. |
Pendule chargé dans un champ électrique :
-
Champ électrique uniforme horizontal,
-
Valeur : E = 2,0 × 104
V . m–1
-
Pendule électrique :
-
Angle α par rapport à sa
position d’équilibre verticale :
-
α = 10 °
-
Système : Boule
-
Charge électrique q ?
-
Masse : m = 0,10 g.
-
g = 10 m . s–2. 1.
Schéma en précisant le signe de la charge
q. 2.
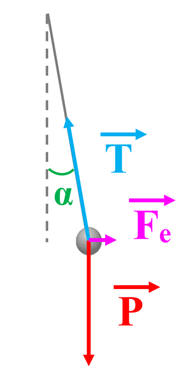
Étude de la boule du pendule : a.
Bilan des forces s’exerçant sur la boule.
-
Schéma :
-
Système d’étude : La boule
-
Référentiel d’étude : Référentiel
terrestre supposé galiléen
-
Tension du fil :
Direction
Celle du fil
Sens
Vers le haut
Valeur
T
-
Force électrique :
Direction
Horizontale
Sens
Gauche à droite
Valeur
Fe
= q . E
-
Poids de la boule :
Direction
Verticale
Sens
Vers le bas
Valeur
P
= m
. g
b.
Loi d’équilibre d’un solide soumis à trois
forces.
-
D’après la réciproque du principe de
l’Inertie, la boule est soumise à des actions mécaniques qui se
compensent :
-
-
Les trois forces sont coplanaires et
concourantes.
-
Valeur du poids :
-
P =
m .
g
-
P = 0,10 × 10–3
× 10
-
P = 1,0 × 10–3
N c.
Force électrique s’exerçant sur la boule.
-
d.
Valeur de la charge q.
-
La charge q est positive :
-
Fe = |q|
. E =
q .
E
-
-
Valeur de la tension T du
fil :
-
![]()
![]()
![]()
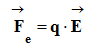
![]()
![]()
![]()
![]()
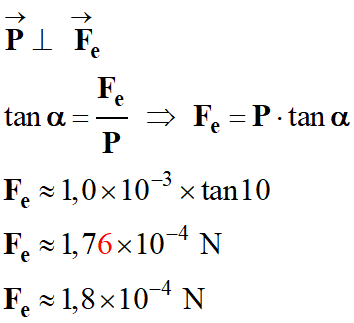
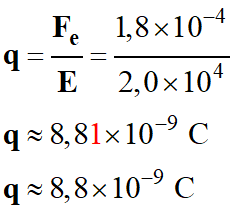
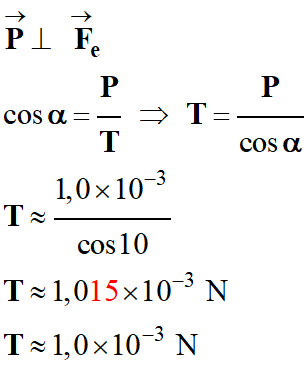
![]()
5)- Exercice 28 : Expérience de Millikan :
|
Expérience de Millikan : On veut superposer au champ de gravitation qui s’exerce sur des gouttes d’huile électrisées négativement un champ électrique uniforme. On utilise pour cela un dispositif constitué De deux plaques
métalliques planes et parallèles, reliées à une source de tension
continue. 1.
: a.
Représenter sur un schéma la disposition des
plaques et des lignes de champ pour s’opposer à l’effet de la
gravitation sur les gouttes d’huile. b.
La tension entre les plaques distantes de
7,0 mm est de 24 V. Calculer la valeur du champ électrique
2.
L’une des gouttes, de rayon r = 0,88
× 10–6 m et de masse volumique ρ = 0,80 kg . dm–3,
reste alors en équilibre. a.
Calculer la valeur de la force électrique
exercée sur la goutte. b.
Calculer la valeur de la charge électrique
portée par la goutte.
-
Donnée : g = 9,8 m . s–2. |
|
Expérience de Millikan : 1.
: a.
Schéma la disposition des plaques et des
lignes de champ.
b.
Valeur du champ électrique
-
La tension entre les plaques : UAB
= 24 V
-
Distantes entre les plaques :
-
d
= 7,0 mm
-
Caractéristiques
du champ électrique
-
Relation :
-
Valeur du champ :
-
2.
Équilibre d’une goutte :
-
Rayon de la goutte :
-
r
= 0,88 × 10–6 m
-
masse volumique de la goutte :
-
ρ = 0,80 kg . dm–3
-
Donnée : g = 9,8 m . s–2.
-
Système d’étude : La goutte d’huile.
-
Référentiel d’étude : Référentiel
terrestre supposé galiléen
-
Bilan des forces :
-
FForce électrique :
-
PPoids de la boule :
-
D’après la réciproque du principe de
l’Inertie, la boule est soumise à des actions mécaniques qui se
compensent :
-
-
Les deux forces ont la même ligne
d’action.
-
Volume de la goutte :
-
-
Masse de la goutte :
-
-
P = 0,10 × 10–3
× 10
-
P = 1,0 × 10–3
N
-
Poids de la goutte :
-
-
Application numérique :
-
a.
Valeur de la force électrique exercée sur la
goutte.
-
Les deux forces sont égales et
opposées :
-
Fe =
P ≈ 2,2 × 10–14 N b.
Valeur de la charge électrique portée par la
goutte.
-
Fe = |q|. E
-
Fe = |q|. E =
P ≈ 2,2 × 10–14
N
-
-
q est négatif :
-
q = –
n .
e
-
n ≈ 41 électrons
-
Le but de l’expérience de Millikan,
datant de 1909, était de mesurer la
valeur de la charge électrique portée
par un l'électron.
-
La charge électrique portée par une
goutte d'huile chargée est toujours un multiple entier positif ou
négatif de cette valeur fondamentale e. |
||||||||||||||||||||||||||||||||
|
|