Bac Blanc : Physique N° 1 énoncé et correction De Képler, Galilée et Newton à Voyager…

1. Galilée et la chute libre (1564 - 1642).

En laissant tomber un objet de la tour de Pise, Galilée constate que la durée de chute est de 1,01 s pour une hauteur de chute de 5 mètres. Huyghens fait la même constatation à Londres. 1.1. Montrer que l'accélération de ce mouvement est égale à l'intensité du champ de gravitation, g0, au niveau du sol. - Le système étudié : S = {objet} - Le référentiel d'étude : La tour de Pise, référentiel terrestre supposé galiléen (la durée de l'expérience est courte). - Bilan des forces : le système est soumis à la force de gravitation F - Théorème du centre d'inertie : -  Dans un référentiel Galiléen, la somme des vecteurs forces extérieures appliquées à un solide est égale au produit de la masse du solide par le vecteur accélération de son centre d'inertie. -  On écrit : -  1.2. En déduire la valeur de l'intensité g0 du champ de gravitation au niveau du sol. -  Il faut utiliser les lois de la chute libre : -

2. Newton et le mouvement de la Lune (1647 - 1727).

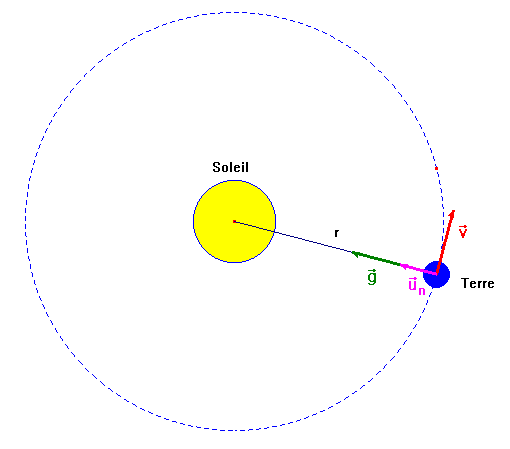
En 1666, Newton étudie les caractéristiques du vecteur accélération d'un mobile animé d'un mouvement circulaire uniforme, puis les utilise pour le mouvement de la Lune qui décrit une orbite circulaire de rayon r = 60 RT en 27 jours 7 heures 43 minutes et 11 secondes.   2.1. Tester vos connaissances sur le mouvement circulaire uniforme : répondre par Vrai ou Faux - Justifier. 2.1.1. L'accélération est nulle car la vitesse est constante ?  Faux, l'accélération n'est pas nulle, elle est centripète car le mouvement est circulaire uniforme. Le vecteur vitesse garde la même valeur, mais il change de direction à chaque instant.  2.1.2. L'accélération est normale, car la norme de la vitesse ne change pas ?  Faux, l'accélération est normale car le mouvement est circulaire uniforme. 2.1.3. L'accélération est constante ?  Faux , si on parle du vecteur accélération et Vrai si on parle de la valeur. La valeur de l'accélération ne change pas : Mais le vecteur accélération change de direction à chaque instant.  2.1.4. La norme du vecteur accélération ne change pas si la vitesse est multipliée par 2 ainsi que le rayon de l'orbite ? Faux, l'accélération est multipliée par deux.  2.2. Calculer la vitesse de la Lune sur son orbite et en déduire la norme de son vecteur accélération (distance Terre - Lune r = 382000 km). Vitesse de la lune :  2.3. En utilisant la deuxième loi de Newton, en déduire la valeur de l'intensité du champ de gravitation créé par la Terre au niveau de la Lune.  Valeur de l'intensité du champ de gravitation : il faut utiliser la deuxième loi de Newton : théorème du centre d'inertie (voir question1.1)

3. Loi de gravitation universelle.

Après que l'astronome français Picard (1671) eut mesuré le rayon de la Terre avec la méthode d'Ératosthène (-II siècle av JC) RT = 6378 km, Newton put enfin conclure.  3.1. Établir comme l'a fait Newton, en utilisant les résultats des questions 1.2 et 2.3, la relation entre l'intensité du champ de gravitation créé par la Terre et la distance (r) du point considéré au centre de la terre. Il faut comparer : .On remarque que :

4. Loi de Kepler (1571 - 1630) et masse du Soleil (M_S).

Kepler, un siècle avant Newton publie (1627) "Les tables Redolphines", résultat de ses nombreuses observations et mesures sur le mouvement des planètes autour du soleil dont voici un extrait.

 

4.1. Représenter graphiquement T2 en fonction de r3. En déduire, comme le fit Kepler dans son "Épitome", la relation entre T2 et r3 ?  L'allure du graphique permet de conclure que le carré de la période est proportionnelle au cube du rayon de l'orbite de la planète considérée. C'est la troisième Loi de Kepler.

4.2. Établir comme le fit Newton, l'expression de la vitesse de la planète, puis de sa période T en fonction de G, MS (masse du Soleil) et r (rayon de l'orbite de la planète autour du Soleil).  Expression de la vitesse de la planète : Le mouvement de la planète autour du Soleil est circulaire uniforme. Expression de la période T : Temps mis par le satellite du Soleil pour faire un tour.  4.3. Déduire des deux questions précédentes la masse du Soleil MS.  Données : G = 6,97 x 10 – 11 S.I (mesuré par Cavendish en 1795)  Masse du Soleil :

5. La gravitation de l'Espace.

La sonde "Voyager" à destination de Saturne et de Titan a fait des mesures du champ de gravitation créé par Jupiter lors de son passage au voisinage de Jupiter. On a ainsi trouvé : g1 = 0,243 m / s² pour une altitude h1 = 650000 km et g2 = 1,040 m / s² pour une altitude h2 = 278000 km.  5.1. Ces résultats sont-ils compatibles avec la loi d'attraction universelle ? Justifier.  Données pour JUPITER : - m = 1,889 x 1027 kg - RJ = 7,14 x 107 m. En conséquence, les résultats expérimentaux sont compatibles