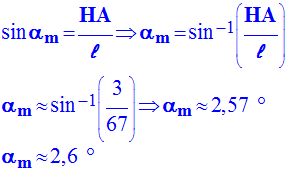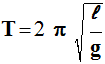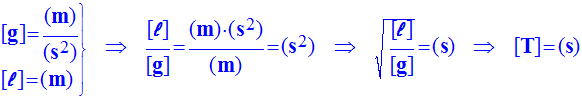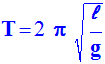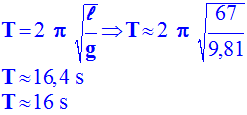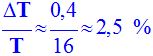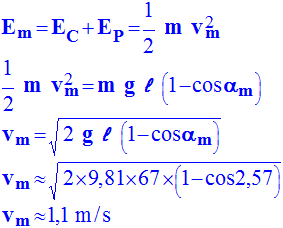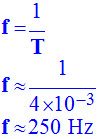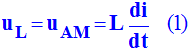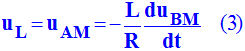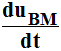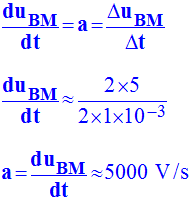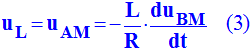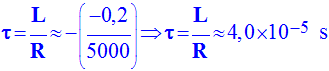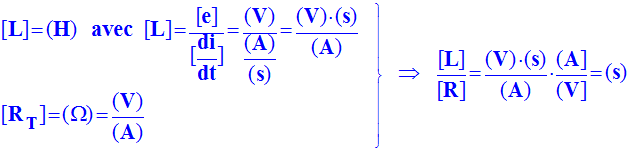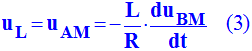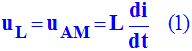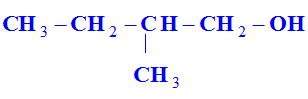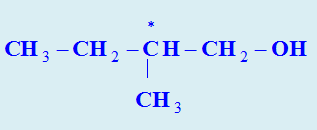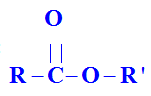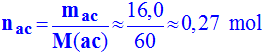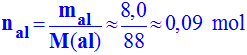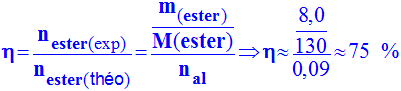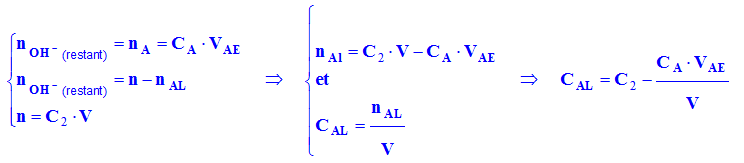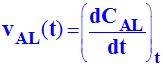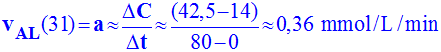|
Bac Blanc |
|
|
A- Exercice
1 (6 pts) : Le pendule de Foucault.
I- Les
oscillations du pendule.
B- Exercice
2 (5 pts) : Une drôle de bobine. |
A- Exercice 1 (6 pts) : Le pendule de Foucault.
Pour permettre d'apporter une preuve expérimentale de la rotation de la Terre sur elle-même,
Foucault imagina plusieurs expériences qui utilisent les propriétés du pendule simple.
Celle réalisée au Panthéon eut un grand succès populaire.
Il fit connaître sa découverte à l'Académie en 1851 ; voici des extraits du texte de sa communication :
|
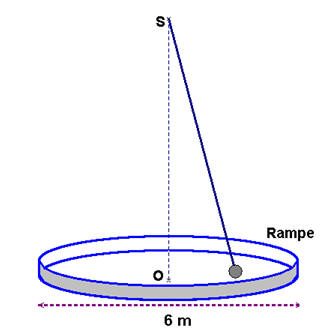
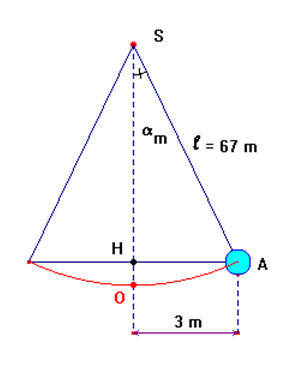
" Le mouvement de la Terre sur elle-même est ici rendu évident au moyen d'un grand pendule, dont le fil attaché au sommet de la coupole descend jusqu'au niveau de la rampe et porte à son extrémité inférieure une boule formée d'une enveloppe de cuivre renfermant une masse de plomb qui le remplit complètement. Le fil a 67 mètres de long…; la boule pèse 28 kilogrammes…Quand il est au repos, le pendule marque le point de centre commun à la table et au grand cercle de bois (rampe) qui l'entoure. Ce
cercle a 6 m de diamètre…"
"…Si on éloigne de sa position d'équilibre la masse du pendule et si on l'abandonne à l'action de la pesanteur sans lui communiquer aucune impulsion latérale, son centre de gravité repassera par la verticale, et, en vertu de la vitesse acquise, il s'élèvera de l'autre côté de la verticale à une hauteur presque égale à celle d'où il est parti. Parvenu à ce point, sa vitesse expire, change de signe, et le ramène, en le faisant encore passer par la verticale, un peu au‑dessous de son point de départ. Ainsi l'on provoque un mouvement oscillatoire de masse pendulaire suivant un arc de cercle dont le plan est nettement déterminé et auquel l'inertie de la masse assure une position invariable dans
l'espace". "Ce pendule, le plus grand qui ait été construit jusqu'ici, donne une oscillation de huit secondes ; il faut seize secondes en effet pour aller et venir. Quoique ces oscillations diminuent d'amplitude assez rapidement, au bout de cinq à six heures,
elles sont encore assez grandes… Pour lancer le pendule on écarte la "boule" jusqu'au bord du grand cercle en bois et on le lâche sans vitesse initiale…et, pour voir comment il marche, on place sur le rebord du cercle de bois deux bancs (tas) de sable humide, fraîchement moulés. Ils sont alignés selon la course du pendule. Celui-ci pratique en passant sur chacun d'eux, une petite brèche qui s'agrandit de plus en plus tant que les oscillations dépassent le cercle de bois. L'agrandissement de la brèche a toujours lieu vers la gauche de la personne qui regarde vers le centre, comme si le plan d'oscillation tournait de droite à gauche…" |
Dans toutes les expressions littérales on notera ℓ la longueur du fil, m la masse de la "boule".
Pour les applications numériques, on prendra g = 9,81 m / s².
I- Les oscillations du pendule.
|
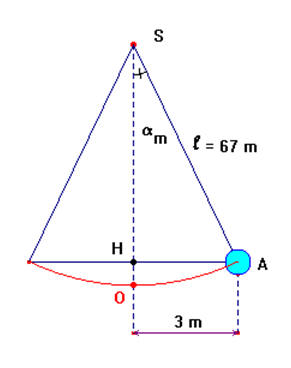
1)- Vérifier que l'amplitude angulaire maximale donnée au pendule est : αm ≈ 2,6 °.
-
L’amplitude angulaire maximale :
-
-
Schéma :
2)- Le mot "oscillation" utilisé par Foucault dans le passage "donne une oscillation de huit secondes" vous paraît-il correctement employé ? Pourquoi ? - Le mot «oscillation» employé par Foucault correspond à une demi-oscillation car une période d’oscillation correspond à durée entre
deux passages
successifs dans la même position et dans le même sens. 3)- .
a)-
La période des petites oscillations pour un
pendule simple a pour
expression :
-
Analyse dimensionnelle :
-
L’expression
b)- Calculer la période d'oscillation d'un pendule simple ayant même longueur de fil que le pendule de Foucault. En comparant cette valeur à celle de la période du pendule de Foucault, peut-on assimiler ce dernier à un pendule simple ? Justifier.
-
Période des oscillations :
-
-
« il
faut seize secondes en effet pour aller et venir »,
-
-
La
période du pendule de Foucault est proche de celle d’un pendule simple.
-
La
différence est surtout due à l’incertitude sur la longueur du pendule. |
|
1)- Le pendule est écarté de sa position de repos de l'angle αm et lâché sans vitesse initiale. L'énergie potentielle du système S = {pendule, Terre} est choisie égale à zéro pour une position de repos du pendule. a)- Sous quelles formes le système étudié possède-t-il de l'énergie ?
-
Le système
S possède de l’énergie cinétique
EC et de
l’énergie potentielle de pesanteur EP. b)- Exprimer littéralement l'énergie mécanique de ce système au moment où on lâche le pendule. Calculer sa valeur. Faire un schéma légendé explicatif. Schéma :
-
Énergie du système
S à l’instant initial : comme on lâche le
pendule sans vitesse initiale, son énergie cinétique EC
est nulle.
-
Il possède de
l’énergie potentielle de pesanteur uniquement :
-
Em = Ep = m . g . h = m . g .OH
= m . g .
ℓ . (1 – cos α)
-
Em =
28
× 9,91
×
67
×
(1 – cos 2,57)
-
Em
≈ 18,5 J 2)- On veut calculer la valeur de la vitesse vm de "la boule" (considérée comme un point matériel) au premier passage par le point le plus bas de sa trajectoire après sont lancement. a)- Quelle hypothèse doit-on faire sur l'énergie mécanique du système pour effectuer ce calcul ?
-
Hypothèse : on
considère que sur ce trajet les frottements sont négligeables et que
l’énergie mécanique
du système S = {pendule, Terre}
se conserve. b)- Cette hypothèse étant supposée admise, calculer la valeur de la vitesse vm.
-
Au
point O, la vitesse du pendule est maximale car l’énergie
potentielle de pesanteur du sytème
S est minimale
-
L’énergie
potentielle est nulle au point O car l'énergie potentielle du
système
S = {pendule, Terre} est choisie égale à zéro pour une
position de repos du pendule.
-
3)- Interpréter, en termes de transferts d'énergie, l'évolution de la vitesse du pendule décrite dans le deuxième paragraphe du texte de Foucault.
-
À
l’instant t = 0 s, le système
S ne possède que de
l’énergie potentielle de pesanteur.
-
Au
cours du mouvement cette énergie potentielle de pesanteur
diminue
jusqu’à la position d’équilibre tandis que l’énergie cinétique augmente.
-
Lorsque le pendule remonte, l’énergie cinétique diminue jusqu’à
s’annuler et l’énergie potentielle augmente jusqu’à sa valeur maximale.
|
|
1)- L'expérience de Foucault est reprise actuellement au Panthéon. On utilise un pendule de même longueur, de mêmes dimensions, mais de masse 47 kg. Parmi les grandeurs suivantes, indiquer celles qui sont modifiées et dans quel sens : (on justifiera la réponse sans calcul numérique) a)- La période du pendule.
-
La période du
pendule simple
-
On peut
assimiler le pendule de Foucault à un pendule simple. b)- L'énergie mécanique initiale du système.
-
Em = Ep = m . g . h = m . g .OH = m . g .
ℓ . (1 – cos αm)
-
Seule la masse
du pendule a changé.
-
L’énergie
mécanique initiale est proportionnelle à la masse du pendule.
-
L’énergie
mécanique initiale est plus grande car on remplace une boule de 28 kg
par une boule de 47 kg. c)- La valeur de la vitesse vm au passage par la position d'équilibre.
-
-
La
valeur de la vitesse ne dépend pas de la masse. Elle ne change pas. 2)- . a)- Quelle propriété du pendule, évoquée dans le texte permet de mettre en évidence la rotation de la Terre ? - Le plan d’oscillations devrait être fixe, or on s’aperçoit que le plan d’oscillation tourne : « le plan est nettement déterminé et auquel l'inertie de la masse assure une position invariable dans l'espace » ,
« le plan d'oscillation tournait de droite à gauche ». b)- Quelle observation faite au moment de l'expérience permet de conclure "Bien sûr qu'elle tourne !" ?
-
Foucault observe une rotation du plan d’oscillation du pendule attribuée
à la rotation de la terre. |
B- Exercice 2 (5 pts) : Une drôle de bobine.
|
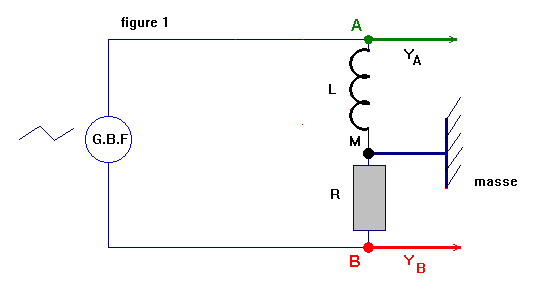
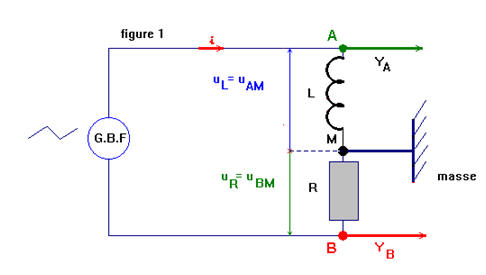
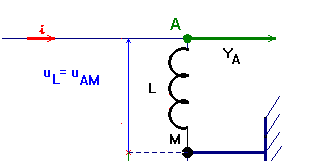
On dispose d'un générateur de signaux basses fréquences délivrant une tension alternative triangulaire symétrique. On associe ce générateur G, dont la masse est isolée de la terre, en série avec une bobine d'inductance L, de résistance négligeable, et un conducteur ohmique de résistance R = 2200 Ω (figure 1). On relie la masse de l'oscilloscope bicourbe au point M, la voie A au point au point A, la voie B au point B. La masse de l'oscilloscope est, par sécurité reliée à la terre.
-
On doit utiliser un
G.B.F avec une « masse flottante », c’est-à-dire
que la masse du
G.B.F doit être isolée de la terre.
-
Car autrement,
cela revient à court-circuiter un dipôle du circuit, soit le conducteur
ohmique, soit la bobine. 2)- . a)- quelle est la grandeur électrique observée à la voie A ? Quelle est celle observée à la voie B ? Reproduire le schéma électrique sur la copie et représenter les grandeurs électriques précédentes.
-
À la
voie A, on observe la tension
uAM, tension aux
bornes de la bobine.
-
À la voie B,
on observe la tension uBM, tension aux bornes du
conducteur ohmique.
-
Schéma :
b)- Les réglages de l'oscilloscope sont les suivants : |
|
Sensibilité verticale
voie A |
200 mV / div |
|
Sensibilité verticale
voie B |
5 V / div |
|
Durée de balayage
horizontal |
1 ms / div |
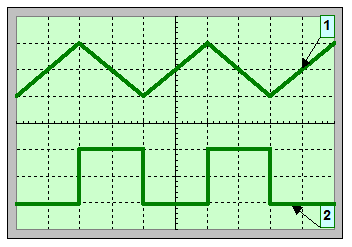
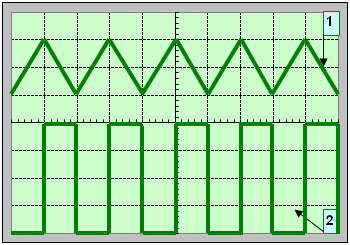
Après avoir réglé les niveaux zéros des deux voies (voir figure 2), les oscillogrammes obtenus sont représentés dans la figure 3.
|
Avant |
|
|
Figure 2 |
Figure 3 |
|
Après (avec les mêmes réglages) |
|
|
Quelle est la fréquence de la tension délivrée par le générateur. Expliquer comment vous procédez pour la déterminer. -
à
l’aide de l’oscillogramme, on peut déterminer la période du
phénomène : - T = b . x
-
T
≈ (1 ms / div) . (4 div) - T ≈ 4 ms
-
On peut en
déduire la fréquence des oscillations :
-
3)- . a)- Nommer le phénomène mis en évidence dans cette expérience. Expliquer qualitativement ce qui se passe dans la bobine.
-
Le
phénomène physique mis en évidence dans cette expérience est le
phénomène d’auto-induction.
-
Lorsque une
bobine est parcourue par un courant variable, celle-ci s’oppose aux
variations du courant.
-
La bobine est
le siège d’une f.é.m induite qui s’oppose au phénomène qui lui a donné
naissance.
-
Elle crée un
courant induit qui s’oppose soit à l’augmentation soit à la diminution
du courant dans le circuit. b)- Établir la relation entre la tension uAM aux bornes de la bobine, l'inductance L et l'intensité instantanée i circulant dans le circuit. Faire un schéma détaillé et préciser le sens du courant.
-
Schéma :
-
Tension aux bornes de la bobine :
-
c)- Établir la relation entre uAM et uBM en utilisant la loi d'ohm aux bornes d'une bobine et la loi d'Ohm aux bornes d'un conducteur ohmique.
-
Tension aux bornes
du conducteur ohmique :
-
uR = uBM = –
R . i
(2)
-
En combinant
(1) et (2) :
-
d)- Des deux oscillogrammes 1 et 2, retrouver celui qui correspond à la voie A et celui qui correspond à la voie B.
-
La
tension aux bornes de la bobine est proportionnelle à la dérivée de la
tension aux bornes du conducteur ohmique.
-
La tension en
créneaux correspond à la dérivée de la tension triangulaire.
-
L’oscillogramme (1) correspond à
la voie B (uR) et l’oscillogramme (2)
correspond à la voie A (uL = uAM). 4)- En utilisant les réglages de l'oscilloscope : a)- Déterminer les valeurs extrêmes de la tension uAM aux bornes de la bobine.
-
Valeurs
extrêmes de uAM.
-
(uAM)max
≈ 200 mV
et
(uAM)min ≈
– 200 mV
b)-
À partir de la première demi période des
oscillogrammes de la figure 3, calculer :
-
On
travaille sur la première demi période :
-
la tension
uBM
est du type :
uBM =
a . t
-
La grandeur
a représente le coefficient directeur du premier segment
de droite.
-
En
conséquence :
-
5)- .
a)-
Déduire des questions 3)-. et 4)-. la valeur
numérique du rapport :
-
De la
relation (3) du 3)- c)- :
-
- uAM ≈ – 200 mV lors de la première demi-période et -
a ≈ 5000
V / s
-
b)- Que représente cette grandeur ? Justifier que cette grandeur t est bien de même dimension qu'une durée.
-
La grandeur
-
Analyse
dimensionnelle :
-
La grandeur
c)- En déduire la valeur de l'inductance L de la bobine.
-
Inductance
de la bobine :
-
L
= τ . R - L ≈ 4,0 x 10 – 4 × 2200 - L ≈ 88 mH d)- On règle la fréquence du générateur sur 500 Hz sans modifier l'amplitude du signal délivré. Quelle est l'influence de la fréquence sur la tension uBM ? et uBM.
-
- Si la fréquence augmente, le terme augmente aussi, en conséquence,
la valeur
de la tension uAM augmente c’est-à-dire que
(uAM)max
et (uAM)minn
augmentent.. |
C- Exercice 3 (5 pts) : Une odeur de banane.
|
Un alcool commercial est un mélange de deux isomères de formule brute C5H12O, essentiellement l’alcool isoamylique A de formule :
et en faible quantité le 2-méthylbutan-1-ol, alcool B.
1)- a)- Donner le nom systématique de l’alcool A et la formule semi-développée de l’alcool B.
-
Nom de l’alcool
A :
3-méthylbutan-1-ol
-
Formule semi-développée de l’alcool
B :
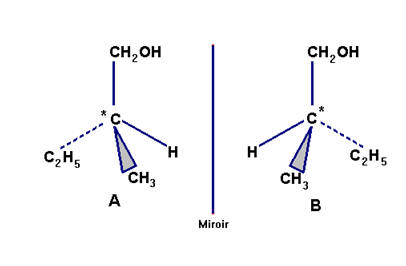
b)- Une de ces molécules possède-t-elle un atome de carbone asymétrique ? Si oui, laquelle ? Représenter les deux énantiomères selon la convention de Cram. A quel type de stéréoisomérie cela correspond-il ?
-
La
molécule B possède un carbone asymétrique :
|
|
-
C’est une
isomérie de configuration. -
Il faut rompre
des liaisons pour passer d’un énantiomère à l’autre.
2)- a)- Écrire l’équation-bilan de la réaction entre l’acide éthanoïque et l’alcool isoamylique A. (On note C et D les produits formés). Quel nom porte une telle réaction ? Quelles sont ses caractéristiques ?
-
Type
de réaction et caractéristiques :
-
On
est en présence d’un équilibre chimique :
-
C’est
une réaction d’estérification : elle est limitée, lente et athermique. b)- Indiquer le nom de chaque produit formé sachant que C dégage une odeur de banane. Préciser la fonction de C. - Le composé C est l’ester : l’éthanoate de 3-méthylbutyle. -
La
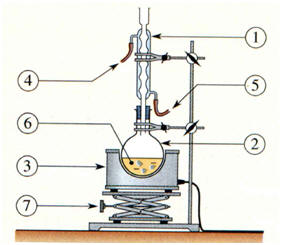
fonction ester : 3)- On mélange 16,0 g d’acide acétique pur, 8,0 g d’alcool isoamylique et 0,5 g d’acide sulfurique. On chauffe à reflux environ 1 heure. a)- Faire le schéma annoté du montage. Quel est l’intérêt d’un tel montage ? |
Schéma du montage :
|
Chauffage à
Reflux
|
1-
réfrigérant. 2-
Ballon.
3-
Chauffe-ballon.
4-
Sortie de l’eau. 5-
Arrivée de l’eau.
6-
Mélange réactionnel.
7-
Vallet ou Support. |
|
-
Le
chauffage à reflux.
-
Il
permet de condenser les vapeurs des réactifs et des produits dans le
réfrigérant
et de les faire retourner à l’état liquide dans le ballon.
-
Les
réactifs et les produits se trouvent dans le milieu réactionnel.
-
Il
permet d’éviter les pertes par évaporation b)- Pourquoi chauffe-t-on ?
-
On
chauffe pour accélérer la réaction qui est lente à température ambiante c)- Quel est le rôle de l’acide sulfurique ?
-
L’acide sulfurique joue le rôle de catalyseur.
-
Il
permet d’augmenter la vitesse de réaction et d’atteindre plus rapidement
l’équilibre chimique sans le déplacer.
d)- Calculer les quantités de matières initiales des réactifs. Ceux-ci sont-ils introduits en proportions stœchiométriques ? Sinon, pour quelle raison ?
-
nac
> nal :
-
Les
réactifs ne sont pas dans les proportions stœchiométriques.
-
Le
fait de mettre de l’acide en excès permet de déplacer l’équilibre dans
le sens de l’estérification et d’augmenter le rendement de cette
réaction. 4)- Après refroidissement du mélange, on le transvase dans une ampoule à décanter. On ajoute de l’hydrogénocarbonate de sodium puis on enlève la phase aqueuse. On peut ensuite prélever le corps C et le sécher avec du sulfate de magnésium anhydre. Après filtration sous büchner, on obtient 8,8 g de C. a)- Faire les schémas correspondant aux étapes successives de manipulation.
-
Schéma : ampoule à décanter et büchner : |
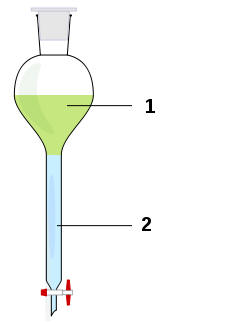

|
-
1 :
Phase organique, principalement l’ester. -
2 :
Phase aqueuse, principalement l’eau. b)- Dans le traitement par la solution d’hydrogénocarbonate de sodium, quel composé réagit avec les ions hydrogénocarbonate ? Quel est l’intérêt de cette manipulation ?
-
Le
but du traitement par la solution d’hydrogénocarbonate de sodium est de
faire réagir l’acide éthanoïque pour le retirer de la phase
organique.
-
Équation bilan :
HCO3–
+
CH3COOH
→ (CO2,
H2O)
+
CH3COO–
-
L’ion
éthanoate est hydrosoluble, il passe dans la phase aqueuse. c)- Calculer le rendement de la réaction étudiée. Commenter le résultat.
-
Le
rendement de la réaction se calcule par rapport au réactif introduit par
défaut :
-
-
Le
rendement est de 66% avec un alcool primaire lorsque les réactifs sont
dans les proportions stœchiométriques.
-
Ici
le rendement est supérieur à 66 % car on utilise un excès d’acide.
Données :
Masses
molaires de l’alcool A : 88 g/mol ; de l’acide éthanoïque : 60 g/mol ;
du corps C : 130 g/mol.
|
D- Exercice 4 (4 pts) : la Saponification
|
On étudie la saponification de l’éthanoate d’éthyle. A la date t = 0, on réalise une solution aqueuse contenant les deux réactifs en volume égal avec des concentrations C1 = 5 × 10 –2 mol/L pour l’éthanoate d’éthyle et C2 = 5 × 10 –2 mol / L pour l’autre réactif. Le mélange est maintenu à la température de 30°C. Des prises d’essai, de V = 10 mL chacune, sont effectuées à différents instants. Un indicateur coloré approprié permet de doser les ions hydroxyde restants par une solution aqueuse d’acide chlorhydrique de concentration CA = 1 × 10 –2 mol/L. Soit VAE le volume de solution acide utilisée pour réaliser ce dosage à l’instant de date t. Les résultats sont consignés dans le tableau suivant : |
|
t (min) |
4 |
9 |
15 |
24 |
37 |
53 |
83 |
143 |
|
VAE (mL) |
44,1 |
38,6 |
33,7 |
27,9 |
22,9 |
18,5 |
13,6 |
8,9 |
|
1)- Donner l’équation-bilan de la réaction de saponification étudiée. Préciser le nom de chaque corps. Quels adjectifs qualifient cette réaction ? |
|
-
La
réaction de saponification est une réaction lente mais totale. 2)- Quel indicateur coloré utilise-t-on pour le dosage des ions hydroxyde ? Justifier. Donner l’équation-bilan du dosage.
-
On
dose les ions hydroxyde (OH–
), base la plus forte dans l’eau par
une solution d’acide chlorhydrique (acide fort dans l’eau).
-
On
est en présence d ‘un dosage acide fort base forte.
-
À
l’équivalence le pH est égal à 7.
-
L’indicateur le mieux adapté est le
B.B.T car sa zone de virage
contient le point d’équivalence. H3O+ (aq) + HO– (aq) → 2 H2O (ℓ) 3)- Donner l’expression de la concentration d’alcool formé au cours du temps en fonction de C2, CA, V et VAE. |
|
-
À
l’équivalence (lors du dosage) : -
-
Expression :
-
4)- Tracer la courbe représentant les variations de cette concentration d’alcool formé en fonction du temps.
-
Tableau : |
|
t
(min) |
4 |
9 |
15 |
24 |
37 |
53 |
83 |
143 |
|
VAE
(mL) |
44,1 |
38,6 |
33,7 |
27,9 |
22,9 |
18,5 |
13,6 |
8,9 |
|
CAL
(× 10–3 mol / L |
5,9 |
11,4 |
16,3 |
22,1 |
27,1 |
31,5 |
36,4 |
41,1 |
|
Échelles : 1 cm < = > 10 min 1 cm < = > 2 x 10 –3 mol / L 5)- Comment évolue la vitesse de formation de l’alcool au cours du temps Interpréter.
-
La
vitesse de formation de l’alcool diminue au cours du temps.
-
- La vitesse de formation de l’alcool est numériquement égale
à la valeur du
coefficient directeur de la tangente à la courbe
CAL =
f
(t). - Comme la courbe tend vers une asymptote horizontale,
le coefficient directeur
de la tangente à la courbe diminue au cours du temps.
-
En
conséquence, la vitesse de formation de l’alcool
diminue au cours du temps.
-
Graphe : |
|
6)- A quelle date la concentration de l’éthanol sera-t-elle égale à 2,5 × 10–2 mol/L ? Évaluer alors la vitesse instantanée de formation de l’éthanol. -
-
À
partir du graphique :
-
Pour
CAL = 25 mmol
/ L, alors t ≈ 31 min
-
On
trace la tangente à la courbe au point considéré et on calcule la valeur
de son coefficient directeur :
|
Données :
|
Indicateur
coloré |
Zone
de virage |
|
Bleu
de bromophénol |
3,0
- 4,6 |
|
Phénolphtaléine |
8,2
- 10,0 |
|
Bleu
de bromothymol |
6,0
- 7,6 |