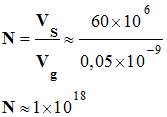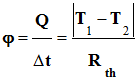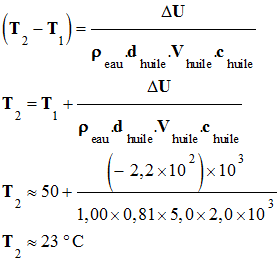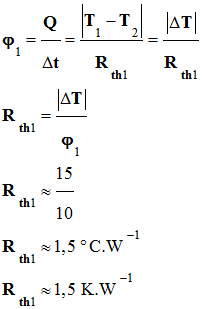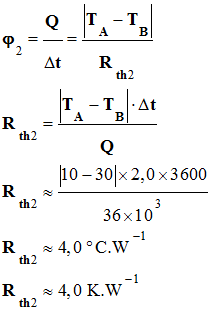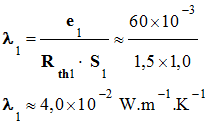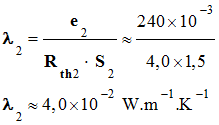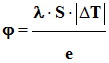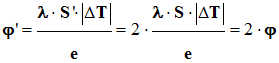1)- Nombre de grains de sable N contenus dans cette dune :

-  Volume d’un grain : V_g = 0,05 mm³

-  Volume du sable : V_S =  60 × 10⁶ m³

-   

2)- Expression  en moles n du nombre de grains de sable contenus dans la dune du Pilat :

-   

3)- Nombre de dunes du Pilat N_D pour avoir une mole de grains de sable :

-   

On considère un corps de masse m dans un état condensé.

Il passe de la température T_i à la température T_f sans changer d’état.

1)- Quand dit-on qu’un corps est dans un état condensé ?

2)- Qu’appelle-t-on capacité thermique massique c d’un corps ? Quel est son unité ?

3)- Quelle est la relation entre la variation d’énergie interne et la variation de température pour un corps dans un état condensé ?

On indiquera les unités des différentes grandeurs.

1)- Corps est dans un état condensé :

-  Les états condensés : état liquide et état solide.

-  Les particules qui constituent le solide ou le liquide (molécules, atomes ou ions) sont les unes contre les autres.

2)- Capacité thermique massique c d’un corps et son unité :

-  La capacité thermique massique c d’une substance correspond au transfert thermique nécessaire

pour faire varier de 1 ° C (ou 1 K) une masse de 1 kg de la  substance.

-  Unité : (J.kg ^{– 1}.° C^{– 1}) ou (J.kg ^{– 1}.K^{– 1})

3)- Relation entre la variation d’énergie interne et la variation de température pour un corps dans un état condensé :

 Un bain marie utilisé en chimie contient 1,7 L d’eau initialement à une température T₁ = 20 ° C.

Au bout de quelques minutes la résistance chauffante du bain-marie permet d’obtenir

 ce même volume d’eau à une température T₂ = 64 ° C.

-  Calculer la variation de l’énergie interne de ce volume d’eau

-  Données : c_eau = 4,18 × 10³ J.kg ^{– 1}.K^{– 1} ; ρ_eau = 1,00 kg . L^–1.

En été et par beau temps, l’eau d’une piscine est à la température de 25 ° C.

La température de l’air est de 30 ° C et celle du sol qui entoure la piscine est de 17 ° C.

Dans cette situation, donner un exemple où un transfert thermique a lieu :

a)-  Par conduction ;

b)-  Par convection ;

c)-  Par rayonnement.

a)-  Transfert thermique par conduction :

-  Entre la piscine et le sol ;

-  Entre la surface de l’eau de la piscine et la couche d’air qui est en contact avec la surface de l’eau.

b)-  Transfert thermique par convection :

-  Dans l’eau de la piscine

-  Dans l’air.

-  Le transfert thermique par convection se fait dans les fluides.

c)-  Transfert thermique par rayonnement :

-  Entre le Soleil et l’eau de la piscine

-  Entre le Soleil et le sol

-  Entre le Soleil et la piscine.

1)- Schéma :

2)- Valeur du flux thermique à travers la vitre :

-   

3)- Énergie thermique transférée en Δt =  1,25 h :

-  Q = φ . Δt

-  Q ≈ 4,0 × 10^–3 × 1,25 × 3600

-  Q ≈ 1,8 × 10⁷  J

Dans un radiateur à bain d’huile, des conducteurs ohmiques chauffent l’huile qu’il contient.

En refroidissant, cette huile transfère de l’énergie thermique à la pièce dans laquelle se trouve le radiateur.

On considère un radiateur contenant 5,0 L d’huile portée à la température de 50 ° C.

On coupe l’alimentation du radiateur.

Au bout d’un certain temps, l’huile est à la température de la pièce.

L’énergie thermique transférée est de 2,2 x 10² KJ.

-  Données :

-  c_huile = 2,0 × 10³ J.kg ^{– 1}.K^{– 1} ;

-  ρ_eau = 1,00 kg . L^–1 ;

-  d_huile = 0,81.

2)- Quel est le signe de la variation de l’énergie interne de l’huile ?

3)- Quelle est la température de l’huile du radiateur lorsqu’elle atteint celle de la pièce ?

1)- Signe de la variation de l’énergie interne de l’huile :

-  La température de l’huile diminue au cours du temps.

-  L’huile cède de l’énergie au milieu extérieur.

-  L’énergie interne de l’huile diminue.

-  La variation de l’énergie interne de l’huile est négative.

-  ΔU < 0

-  ΔU = – 2,2 × 10² kJ = – 2,2 × 10² × 10³ J

2)- Valeur de la température de l’huile du radiateur lorsqu’elle atteint celle de la pièce :

-  T₁ = 50 ° C

-  Température de l’huile du radiateur lorsqu’elle atteint celle de la pièce : T₂ = ? ° C

-  Variation de l’énergie interne :

-  ΔU =  m_huile . c_huile .ΔT = m_huile . c_eau . (T₂  -  T₁ )

-  ΔU = ρ_eau . d_huile .V_huile . c_huile . (T₂  -  T₁ )

-   

1)- Matériau le mieux adapté pour un vêtement d’hiver :

-  Plus la résistance thermique du matériau est élevée, plus le flux thermique est faible à travers le matériau.

-  Ce dernier empêche le transfert d’énergie à travers lui ; c’est un bon isolant thermique.

-  Un matériau qui a une résistance thermique élevée est un bon isolant thermique.

-  Le matériau le mieux adapté pour l’hiver est celui qui a la résistance thermique la plus élevée, c’est-à-dire le feutre.

2)- Résistance thermique totale de plusieurs matériaux accolés les uns aux autres :

-  Lorsque plusieurs parois sont accolées, la résistance thermique totale R_{th tot} est égale

à la somme des résistances thermiques de chaque paroi.

-  R_{th tot}  = R_th1 + R_th2 + R_th3  + R_th4

3)-  

a)-  Deux vêtements superposés :

-  Lorsque deux vêtements sont superposés, on emprisonne une fine couche d’air entre les deux vêtements.

b)-  Plusieurs vêtements fins plutôt qu’un seul épais pour se préserver du froid :

-  Parmi les exemples de matériaux donnés, on remarque que l’air possède la plus grande résistance thermique.

-  C’est un bon isolant thermique.

-  Le fait de mettre plusieurs vêtements fins permet d’emprisonner plusieurs fines couches d’air entre les vêtements et ainsi d’avoir une meilleure isolation.

-  Ceci n’est pas possible avec un seul vêtement épais.

On peut utiliser de la laine de verre pour isoler la toiture d’une maison.

Plusieurs épaisseurs sont proposées par les fabricants.

Paul et Olivia décident de déterminer la résistance thermique R_th1 d’une surface S₁ = 1,0 m²

d’une laine de verre 1 d’épaisseur e₁ = 60 mm et la résistance thermique R_th2 d’une surface S₂ = 1,5 m²

d’une laine de verre 2 d’épaisseur e₂ = 240 mm.

Paul mesure un flux thermique de 10 W lorsque la différence de température entre les deux faces de la laine de verre 1 est de 15 ° C.

Olivia soumet l’une des faces de la laine de verre 2 à une température T_A = 10 ° C et l’autre face à une température T_B = 30 ° C.

Elle mesure une énergie transférée de 36 kJ à travers la laine de verre 2 pendant une durée de 2,0 h.

1)- Calculer la résistance thermique R_th1 de la laine de verre 1.

2)- Calculer la résistance thermique R_th2 de la laine de verre 2.

Lorsque l’on parle d’isolation thermique, on indique souvent la valeur de la conductivité thermique λ d’un matériau.

Cette grandeur est liée à la résistance thermique d’une paroi plane de surface S et d’épaisseur e par :

Avec e en m, S en m² et R_th  en K . W^–1 ou ° C . W^–1

3)-  

a)-  Quelle est l’unité de la conductivité thermique ?

b)-  Calculer les conductivités thermiques respectives λ₁ et λ₂ des laines de verre 1 et 2.

4)- Pourquoi la conductivité thermique caractérise-t-elle un matériau ?

5)- Exprimer le flux thermique traversant une paroi en fonction de λ, S, e et de l’écart de température entre les deux faces.

6)- Comment le flux thermique évolue-t-il lorsque l’on double la surface S de laine de verre ?

7)- Comment le flux thermique évolue-t-il lorsque l’on double l’épaisseur e de laine de verre ?

8)- Quels conseils peut-on donner à u particulier faisant construire sa maison afin de limiter les pertes d’énergie par la toiture ?

-  Donnée : flux thermique :

1)- Valeur de la résistance thermique R_th1 de la laine de verre 1 :

-  Données :

-  Paul mesure un flux thermique de 10 W lorsque la différence de température entre les deux faces de la laine de verre 1 est de 15 ° C.

-   

2)- Valeur de la résistance thermique R_th2 de la laine de verre 2 :

-  Données :

-  S₂ = 1,5 m² d’une laine de verre 2 d’épaisseur e₂ = 240 mm

-  Olivia soumet l’une des faces de la laine de verre 2 à une température T_A = 10 ° C et l’autre face à une température T_B = 30 ° C.

-  Elle mesure une énergie transférée de 36 kJ à travers la laine de verre 2 pendant une durée de 2,0 h.

-   

3)-  

a)-  Unité de la conductivité thermique λ :

-  λ en (W . m^–1 . K^–1) ou (W . m^–1 . ° C^–1)

b)-  Valeur des conductivités thermiques :

-  Valeur de la conductivité thermique de la laine de verre 1 :

-  Données :

-  S₁ = 1,0 m² d’une laine de verre 1 d’épaisseur e₁ = 60 mm

-   

-  Valeur de la conductivité thermique de la laine de verre 2 :

-  Données :

-  S₂ = 1,5 m² d’une laine de verre 2 d’épaisseur e₂ = 240 mm

-   

4)- Conductivité thermique, grandeur caractéristique.

-  La conductivité thermique λ caractérise un matériau comme sa densité d, sa température de fusion θ_f ,…

-  Elle est propre à ce matériau, elle permet de caractériser le matériau considéré.

-  Exemples :

5)- Expression du flux thermique :

-  et

-  On tire :

-   

6)- Flux thermique et surface de la laine de verre :

-  Lorsque l’on double la surface de la laine de verre, le flux thermique est doublé.

-   

-  Pour S’ = 2 S,

-   

7)- Flux thermique et épaisseur de la laine de verre.

-  Lorsque l’on double l’épaisseur de la laine de verre, le flux thermique est divisé par 2.

-  Pour e’ = 2 e

-   

8)- Les conseils :

-  Pour limiter les pertes d’énergie dues à la toiture, il faut :

-  Limiter la surface de la toiture (autant que possible)

-  Augmenter l’épaisseur de la laine de verre utilisée.