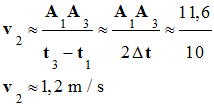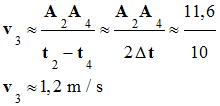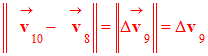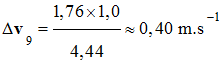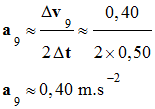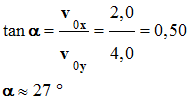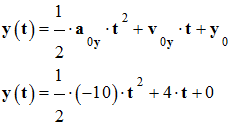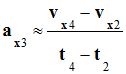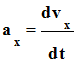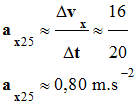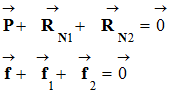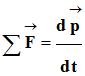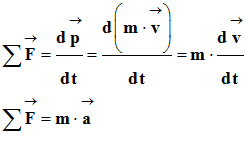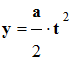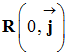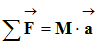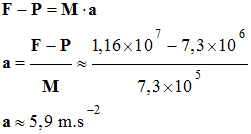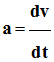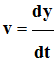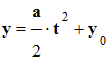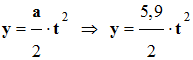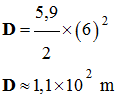|
Chap. N° 05 |
Cinématique et dynamique newtoniennes. Exercices. |
|
 |
I- Exercice 7 page 146 : Choisir un référentiel d’étude.
|
Pour chacune des situations
suivantes, choisir le référentiel d’étude le plus adapté compte tenu du
système : a)-
Terre tournant autour du Soleil ; b)-
Satellite artificiel terrestre ; c)-
Cycliste roulant sur une route ; d)-
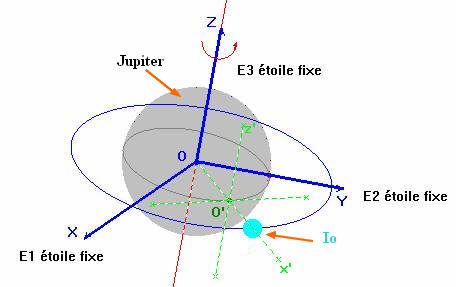
Io en rotation autour de Jupiter. |
|
a)-
Terre tournant autour du Soleil : S
= {Terre} : Référentiel Héliocentrique b)-
Satellite artificiel terrestre ; S
= {Satellite} : Référentiel Géocentrique c)-
Cycliste roulant sur une route : S
= {Cycliste} : Référentiel Terrestre. d)- Io en rotation autour de Jupiter : S = {IO} : Référentiel galiléen lié au centre de Jupiter : Référentiel Jovicentrique (Galilée).
|
II- Exercice 10 page 146 : Connaître les propriétés du vecteur
accélération.
|
On représente à intervalles de temps égaux, les positions successives d’un point A d’une
voiture téléguidée dans un référentiel terrestre. On a obtenu les situations
suivantes : a)-
b)-
c)-
Dans chaque cas, indiquer la
direction et le sens du vecteur accélération du
point A
dans la position
A3. |
|
a)- Le mobile parcourt des distances égales pendant des durées égales. Le mouvement du mobile est rectiligne uniforme. Le
vecteur vitesse est constante et l’accélération est
nulle :
Le mouvement du mobile est rectiligne accéléré : le vecteur accélération a même direction
et même sens que le vecteur vitesse.
c)- Le mobile parcourt des distances de plus en plus petites pendant des durées égales. Le mouvement du mobile est rectiligne retardé : le vecteur accélération a même direction mais un sens opposé au vecteur vitesse.
|
III- Exercice 11 page 147 : Représenter des vecteurs vitesses.
|
On a représenté les positions consécutives d’un point A d’une nacelle d’une grande roue dans un référentiel terrestre. L’intervalle de
temps séparant deux positions consécutives du point
A est Δt =
5,0 s. 1)-
Reproduire la chronophotographie, puis représenter
les vecteurs vitesses
(Préciser
l’échelle choisie pour ces représentations). 2)-
Quelle est la nature du mouvement ?
|
au point A2
et
au point A3. |
1)-
Tracé des vecteurs vitesses.
On peut réaliser les mesures avec Word sur l'image.
2
)-
Nature du mouvement.
-
La trajectoire est
une portion de cercle et la valeur de la vitesse est
constante au cours du temps.
-
Le mobile est animé
d’un mouvement circulaire uniforme.
-
|
||||||||||||||||||||||||||||
IV- Exercice 12 page 147 : Représenter des vecteurs accélérations.
|
On a représenté deux vecteurs
vitesses
L’intervalle de temps
séparant deux positions consécutives du point
A est
Δt = 0,50
s.
1)-
Reproduire le schéma, puis construire au point A9
le vecteur
2)- Calculer la valeur de ce
vecteur à l’aide de l’échelle. En déduire la norme
du vecteur accélération
3)-
Préciser les caractéristiques (direction sens et
valeur) du vecteur accélération
|
et
lors du mouvement d’un point
A dans
un référentiel terrestre. 
.
au
point A9.|
1)-
Tracé du vecteur
2)- Calculer la valeur de ce vecteur à l’aide de l’échelle. En déduire la norme du vecteur
accélération
-
Valeur de
l’accélération a9 :
-
3)-
Préciser les caractéristiques (direction sens et
valeur) du vecteur accélération
-
Caractéristiques de
-
Direction et sens :
les mêmes que - Valeur : a9 ≈ 0,40 m . s–2 |
V- Exercice 16 page 148 : Analyser un mouvement.
|
Les évolutions temporelles des coordonnées vx et vy du vecteur vitesse relatif au mouvement d’une bille lancée vers le haut dans un plan vertical (Oxy)
associé à un repère orthonormé sont représentées
ci-dessous.
1)-
Calculer la valeur de la vitesse de la bille aux
instants t1 = 0,2 s et t2
= 0,6 s. 2)-
Décrire l’évolution de la valeur de la vitesse de la
bille entre 0,0 s et 0,8 s. 3)-
Représenter les évolutions temporelles des
coordonnées ax et ay
de l’accélération de la bille au cours de ce
mouvement. 4)-
En déduire la valeur de l’accélération de la bille à
chaque instant et préciser la nature du mouvement. |
|
1)-
Valeur de la vitesse de la bille aux instants t1
= 0 s et t2 = 0,6 s.
- La valeur de la vitesse est une grandeur positive ou nulle (comme une norme),
alors que les coordonnées du vecteur
vitesse peuvent être positives, négatives ou nulles. 2)-
Évolution de la valeur de la vitesse de la bille
entre 0,0 s et 0,8 s.
-
Au cours du
mouvement :
-
Équations horaires
obtenues à partir du graphique :
-
Pour 0,0 s ≤ t
≤ 0,4 s, la valeur de la vitesse diminue.
-
Pour t > 0,4
s, la valeur de la vitesse augmente. 3)-
Représentation des évolutions temporelles des
coordonnées ax et ay
de l’accélération de la bille au cours de ce
mouvement. - Les coordonnées ax et ay de l’accélération de la bille au cours de ce mouvement sont données
par les
dérivés par rapport aux temps des coordonnées du
vecteur vitesse.
-
L’accélération est
constante au cours du temps.
-
Le vecteur
accélération garde la même direction, le même sens
et la même valeur au cours du mouvement 4)-
Valeur de l’accélération de la bille à chaque
instant et la nature du mouvement.
-
Le mobile est animé
d’un mouvement uniformément varié (retardé, puis
accéléré).
►
Pour aller plus
loin :
-
On peut représenter
le mouvement du mobile dans le plan (Oxy) :
-
Conditions initiales
-
On ne connaît pas la
position du mobile à l’instant initial , on peut
choisir :
-
On connaît les
coordonnées du vecteur vitesse initiale :
-
Coordonnées des
différents vecteurs :
-
Représentation de
x = f (t) et y = g (t) :
-
Représentation de
y = f (x) : Trajectoire du mobile
dans le repère (Oxy).
-
Chronophotographie du
mouvement (Δt = 0,10 s)
|
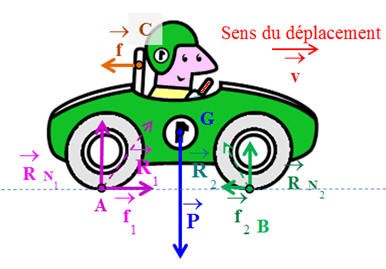
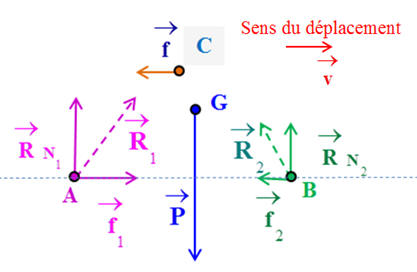
VI- Exercice 18 page 148 : Déterminer des forces inconnues.
|
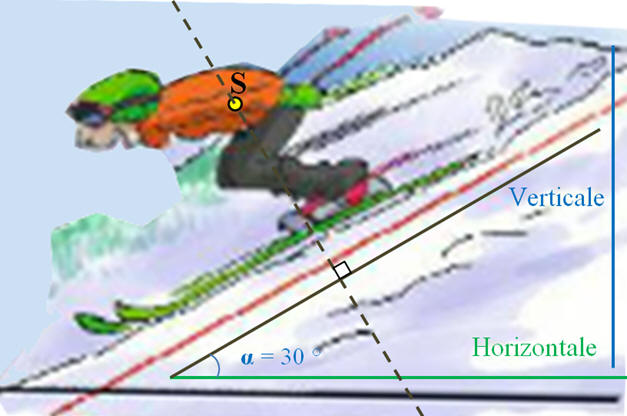
Un skieur de masse M = 60 kg glisse à la vitesse de valeur constante sur une piste rectiligne qui fait un angle α
= 30 ° avec
l’horizontale. Le skieur est modélisé par son centre de gravité S. On
considère qu’il est soumis à trois forces :
-
Son poids
-
L’action normale du
sol
-
Une force de
frottement
1)-
Quelle relation vérifient ces forces ? 2)- Schématiser, à l’échelle 1 cm pour 200 N et en respectant les angles, les vecteurs qui modélisent
ces forces. 3)-
Déduire de la construction les valeurs de
Donnée :
g = 10 N
/ kg. |
;
(perpendiculaire
au plan de la piste) ;
(parallèle à la piste et de sens opposé au
déplacement).|
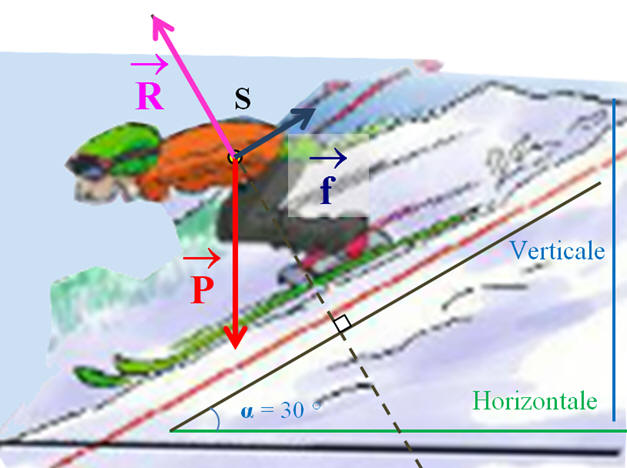
1)-
Relation vérifiée par ces forces :
-
Le référentiel
d’étude est un référentiel terrestre supposé
galiléen.
-
Le système étudié est
le skieur assimilé à un point matériel S de
masse M.
-
Le système matériel
est animé d’un mouvement rectiligne uniforme.
-
D’après la réciproque
du principe de l’inertie : - Le système S est pseudo-isolé, il est soumis à des forces dont les effets se compensent.
-
On peut écrire :
-
2)-
Schéma :
-
On connaît :
-
On connaît les
directions et sens des deux autres forces.
-
Schéma et mesures
réalisées avec Cabri Géomètre II
-
Les mesures :
3)-
Valeurs de
|
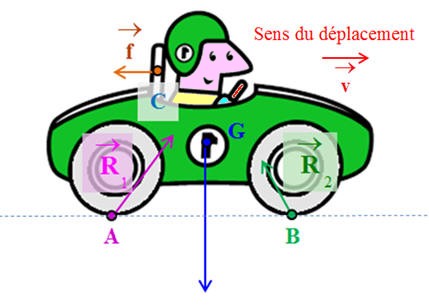
VII- Exercice 28 page 150 : Voiture au banc d’essais.
|
Lors d’une séance d’essais, on enregistre la coordonnée vx de la vitesse d’une voiture de masse
m = 1200
kg pendant une phase de démarrage sur une portion de
route rectiligne. L’axe (Ox)
étant orienté dans le sens du mouvement, on obtient
les résultats suivants :
1)-
Vitesse et accélération. a)-
Représenter l’évolution de
vx en fonction du temps. b)- Repérer et caractériser les 3 phases du mouvement. Décrire qualitativement
l’évolution de la valeur de l’accélération sur
chacune des phases. 2)-
Accélération. a)- Expliquer comment déterminer la coordonnée ax de l’accélération du véhicule à différents instants, à partir de cette
courbe ? b)-
Calculer la valeur de
l’accélération durant la première phase. c)-
Calculer la valeur de
l’accélération à la date t = 25 s. 3)-
En déduire un autre de grandeur de la valeur de la
force motrice de la voiture à t = 25 s. |
|
1)-
Vitesse et accélération. a)-
Évolution de vx
en fonction du temps.
b)-
Les 3 phases du mouvement.
-
Description et
évolution de la valeur de l’accélération sur chacune
des phases.
2)-
Accélération. a)-
Détermination de la
coordonnée ax
-
On peut utiliser la
relation approchée suivante :
-
Autre méthode : on
peut utiliser le fait que - Pour déterminer la valeur ax de l’accélération de la voiture, à un instant donné, à partir de la représentation de vx = f (t), on calcule le coefficient directeur de la tangente à la courbe au point considéré
(on peut s’aider des
points qui encadrent le point considéré)
-
Exemple : ici, on a
tracé la tangente à la courbe au point A9,
à l’instant t = 25 s.
b)-
Valeur de l’accélération
durant la première phase.
-
Durant la première
phase, l’accélération est constante : a ≈ 2,5
m . s–2 c)-
Valeur de l’accélération à
la date t = 25 s.
-
Valeur de
l’accélération à l’aide du tableau : a25
≈ 0,80 m . s–2
-
Valeur de
l’accélération à l’aide de la tangente :
-
3)-
Ordre de grandeur de la valeur de la force motrice
de la voiture à t = 25 s.
-
La masse du système
S est constante au cours du mouvement : - À l’instant t = 25 s, dans un référentiel Terrestres supposé galiléen,
on peut appliquer le théorème fondamental
de la dynamique (deuxième loi de Newton) :
-
On va distinguer 2
types de roues :
-
Les roues motrices
-
Les roues
indépendantes.
-
Cas d’une propulsion
arrière : ce sont les roues arrière qui sont
entraînées par le moteur dans un mouvement de
rotation.
-
Quelle que soit la
roue, il faut des forces de frottement pour que la
roue tourne sans glisser.
-
Bilan des forces :
-
Cas présent : Pour
simplifier l’étude,
-
On néglige les
frottements dus à l’air et la poussée d’Archimède.
-
On ne tient compte
que des frottements solides entre le sol et les
roues.
-
Interaction entre le
sol et la voiture :
-
On la décompose en :
-
La réaction normale
au support
-
La force tangente au
déplacement
-
Le poids de la
voiture :
-
Schéma :
-
-
On remplace
-
Avec
- Dans un référentiel galiléen, si un système assimilé à un point matériel est soumis à une ou plusieurs forces extérieures,
alors la somme vectorielle de ces forces est égale à
la dérivée par rapport au temps de son vecteur
quantité de mouvement :
-
On écrit :
-
La masse du système
se conserve au cours du mouvement : m = cte
-
-
-
En projetant la
relation sur l’axe (Ox), on obtient :
-
Px
+ RNx + fx =
m . ax
-
0 + 0 + f =
m . ax
-
Valeur de la force
f :
-
f ≈ 1200
x 0,80
-
f ≈ 9,6
x 102 N
-
La force de
frottement f résulte de l’action de la route
(asphalte) sur la voiture.
-
La force F,
force motrice de la voiture, résulte de l’action de
la voiture sur la route (asphalte).
-
La troisième loi de
Newton permet d’écrire que :
-
-
-
F = f ≈
9,6
x 102 N
-
Ceci au temps t
= 25 s. |
(sol
; pneu de la roue motrice). 
qui compense une partie du poids et 
qui
fait avancer la moto.
,
la roue non motrice qui tourne,
qui
compense une partie du poids et 
qui fait tourner la roue non motrice
VIII- Exercice 30 page 150-151 : Décollage d’Ariane 5.
|
La fusée Ariane 5 permet de mettre en orbite divers satellites, dont des satellites météo. Lors du décollage, la poussée
des moteurs est modélisée par une force verticale de
valeur constante
F. Tout au long du décollage, on
admet que la valeur du champ de pesanteur
g est
constante. La masse totale de la fusée est
notée M. Dans un référentiel terrestre supposé galiléen, on étudie le mouvement du centre d’inertie G de la fusée. On choisit un repère orthonormé dans
lequel l’axe vertical est dirigé vers le haut. À l’instant
t0
= 0 s, Ariane 5 est immobile au sol et son centre de
gravité G
est confondu avec l’origine
O du
repère orthonormé.
Pendant la phase de décollage, on
suppose que seuls le poids
On néglige l’action de l’air sur la
fusée et on considère que la masse
M de la
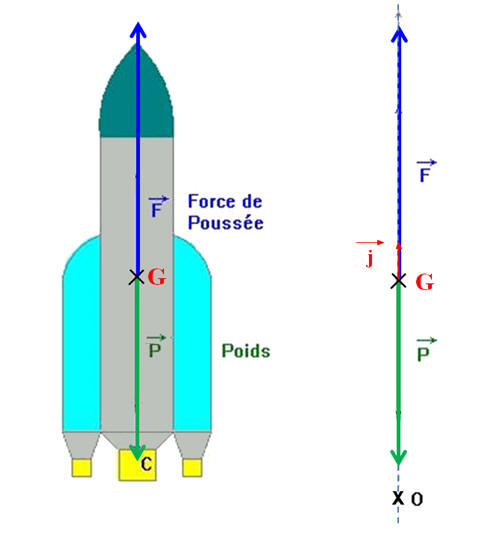
fusée reste constante. 1)- Représenter sur un schéma, à la même échelle, les forces s’exerçant sur la fusée modélisée par le
point G pendant le décollage quand elle a
quitté le sol. 2)-
Établir l’expression de la coordonnée verticale a
de l’accélération du point G. Calculer sa
valeur. 3)-
Parmi les propositions suivantes, laquelle
correspond à l’expression de la coordonnée verticale
v de la vitesse du point G ?
-
v = a .
t
-
v = v .
t
-
v = a .
t2 4)-
Parmi les propositions suivantes, laquelle
correspond à l’expression de la coordonnée verticale
y de la position du point G ?
-
y = 0
-
y = a .
t . y
-
5)- La trajectoire ascensionnelle reste verticale et l’accélération est inchangée jusqu’à la date t1 = 6,0 s. À cette date, quelle est la distance
parcourue depuis le décollage ? 6)-
Par quel principe la propulsion de la fusée est-elle
assurée ? Illustrer la réponse par un schéma. |
agissent
sur la fusée. 
|
1)-
Schéma des forces s’exerçant sur la fusée modélisée
par le point G.
2)-
Expression de la coordonnée verticale a de
l’accélération du point G et valeur.
-
Système étudié :
centre d’inertie G de la fusée de masse M.
-
Référentiel d’étude :
Référentiel terrestre supposé galiléen
-
Bilan des forces : le
poids
- On écrit :
-
Comme la masse
M du système est constante : on
peut écrire que :
-
-
Dans le cas présent :
-
On projette cette
relation sur l’axe (Oy) :
-
Fy
+ Py = M ay
-
Avec les notations
utilisées :
-
3)-
Expression de la coordonnée verticale v de la
vitesse du point G ? - L’accélération est constante.
- La fusée est animée d’un mouvement
rectiligne accéléré.
-
La vitesse est
proportionnelle au temps t.
-
Or :
-
v est une
primitive de a
-
v = a . t + v0
-
D’après les
conditions initiales, la fusée est immobile au temps
t = 0 s, v0 = 0 m / s
-
v = a .
t ou v = 5,9
t 4)-
Expression de la coordonnée verticale y de la
position du point G ?
-
La relation liant la
coordonnée verticale y à la coordonnée
verticale de la vitesse v :
-
-
y est une
primitive de v
-
-
D’après les
conditions initiales, au temps t = 0 s, y0
= 0 m
-
5)-
Distance parcourue depuis le décollage.
-
6)-
Principe de la propulsion de la fusée.
-
La force de poussée
est assurée par l’éjection des gaz de combustion
(gaz issus de la combustion du peroxyde d'azote N2O4)
-
C’est la propulsion
par réaction comme dans le cas du ballon de
baudruche qui se dégonfle. |
IX- Exercice 34 page 152 : En impesanteur.
|
|
|
|
X- Exercice 35 page 153 : Le dauphin à flancs blancs.
|
|
|
|
|
|