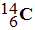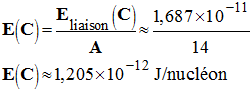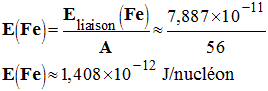|
Phys. N° 05 |
Radioactivité et réactions nucléaires. Exercices. |
|
|
Mots clés : Réaction nucléaire, radioactivité, réactions nucléaires spontanées, réactions nucléaires provoquées, équation d'une réaction nucléaire, lois de conservation, lois de Soddy, énergie libérée, relation Einstein, défaut de masse, énergie de liaison d'un noyau, QCM sur la radioactivité, exercices sur la radioactivité., ... |
 |
Classification périodique :
Cliquer sur l'image pour l'agrandir
I- Exercice 7 page 146. Reconnaître des réactions nucléaires provoquées.
|
Parmi les réactions nucléaires suivantes, repérer les équations des réactions de fission et de fusion : a)-
b)-
c)-
d)-
e)-
|
|
- La réaction de fission nucléaire : - La réaction de fission est une réaction nucléaire provoquée. - Au cours d’une fission nucléaire, un neutron lent (neutron thermique) brise un noyau lourd fissile en deux noyaux légers. - Cette réaction libère de l’énergie. - La réaction a)- est une réaction de fission nucléaire :
- La réaction de fusion nucléaire : - Au cours d’une fusion nucléaire, deux noyaux légers s’unissent pour former un noyau lourd. - C’est une réaction nucléaire provoquée qui libère de l’énergie. - La réaction b)- est une réaction de fusion nucléaire :
- La réaction c)- est une désintégration β+ (émission d’un positon) - La réaction d)- est une réaction de fusion nucléaire.
- La réaction e)- est une désintégration β– (émission d’un électron)
|
II- Exercice 10 page 146. Savoir calculer une activité.
|
En une minute, on a mesuré 5400 désintégrations de carbone 14 dans un échantillon provenant d’une momie. 1)- Quelle est l’activité de cet échantillon ? 2)- Combien aurait-on mesuré de désintégrations en 2,0 minutes ? |
|
1)- Activité de l’échantillon : - L’activité A d’un échantillon radioactif à la date t est le nombre de désintégrations par seconde de cet échantillon. - L’activité A d’un échantillon radioactif diminue au cours du temps. - Cette diminution est caractéristique du noyau radioactif présent dans l’échantillon. -
2)- Nombre N de désintégrations en 2,0 minutes : - Sur cette durée, la diminution de l’activité du carbone 14 est négligeable : - N ≈ 1,08 x 104 désintégrations. |
III- Exercice 11 page 146. Utiliser les lois de conservation.
|
1)- Citer les lois de conservations mises en œuvre dans une réaction nucléaire. 2)- Recopier et compléter les équations des réactions ci-dessous.
a)-
b)-
c)-
d)-
|
|
1)- Lois de conservation : - Toutes les réactions nucléaires vérifient les lois de conservation suivantes :
- Lois de Soddy : - Conservation du nombre de masse : A = A’ + a -
Conservation de la charge :
Z = Z’ + z 2)- Équations :
a)-
- 107 = A et 46 = Z + (–1) - A = 107 et Z = 47
b)-
- 218 = A + 4 et 84 = Z + 2 - A = 214 et Z = 82
c)-
- A = 208 + 0 et Z = 82 + 1 - A = 208 et Z = 83
d)-
- 2 + 2 = A + 1 et 1 + 1 = Z + 0 - A = 3 et Z = 2 |
IV- Exercice 13 page 146. Écrire une équation de réaction nucléaire.
|
Le plomb 185
1)- Le mercure : a)- Quel est le numéro atomique du mercure dont le symbole est Hg ? On pourra s’aider de la classification périodique. b)- Quelle est la représentation symbolique du mercure 181 ? 2)- Écrire l’équation de la réaction nucléaire. |
est
radioactif. Il se désintègre en formant du mercure
181 et un noyau d’hélium.|
1)- Le mercure : a)- Numéro atomique du mercure : -
La formule du noyau d’hélium :
- Au cours de la réaction nucléaire, il y a conservation de la charge : - 82 = Z + 2 - Z = 80 b)-
Représentation symbolique du mercure 181 : 2)- Équation de la réaction nucléaire : désintégration alpha
|
.
V- Exercice 14 page 146. Écrire une équation de réaction de fusion.
|
Écrire l’équation de la réaction de fusion entre deux noyaux d’hélium 3 qui donne un noyau d’hélium 4 et deux noyaux d’hydrogène 1. On pourra s’aider de la classification périodique. |
|
Équation de la réaction :
|
VI- Exercice 15 page 146. Écrire une équation de réaction de fission.
|
Écrire l’équation de la réaction de fission d’un noyau d’uranium 235 qui donne un noyau de zirconium 95, un noyau de tellure 138 et 3 neutrons. On pourra s’aider de la classification périodique : |
|
Équation de la réaction de fission d’un noyau d’uranium 235 :
- Dans la classification périodique, on trouve - Pour le zirconium Zr, Z1 = 40 - Pour le Tellure Te, Z2 = 52
- Cette réaction produit plus de neutrons qu’elle n’en consomme. - Vérification : - (1 + 235 = 95 + 138 + 3 x 1) - (92 = 40 + 52 + 0) |
VII- Exercice 18 page 147. Histoire et radioactivité.
|
Le polonium 210 a été l’un des premiers isotopes radioactifs découverts par Pierre et Marie Curie. Lors de sa désintégration, il donne du plomb et un noyau d’hélium 4. 1)- Quelles sont les représentations symboliques du polonium 210 et de l’hélium 4. On pourra s’aider de la classification périodique. 2)- Écrire l’équation de la réaction en citant les lois utilisées. |
|
1)- Représentations symboliques du polonium 210 et de l’hélium 4 : -
Polonium 210 :
-
Hélium 4 :
2)- Équation de la réaction et les lois utilisées : - Lois de Soddy : - Conservation du nombre de masse. - Conservation de la charge.
- 210 = A + 4 et 84 = Z + 2 - A = 206 et Z = 82
|
VIII- Exercice 20 page 147. De la masse à l’énergie.
|
Le radon 222 se désintègre suivant la réaction :
- Données :
1)- De quel type de réaction s’agit-il ? 2)- Calculer la perte de masse accompagnant cette réaction. 3)- Calculer l’énergie produite par la désintégration d’un noyau de radon 222. |
||||||||||
|
1)- Type de réaction ; il s’agit d’une
désintégration α. - Il y a émission d’un noyau d’hélium au cours de la désintégration du noyau de polonium 210. 2)- Perte de masse : - |Δm| = |m (produits) – m (réactifs)| -
|Δm|
= |m (Po) + m (He) –
m (Rn)| -
|Δm|
≈ |3,6193691x
10–
25 + 6,64466
x 10–
27 –
3,6859160
x 10–
25 | - |Δm| ≈ 1,00300 x 10– 29 kg 3)- Énergie produite : - Eproduite = |Δm| . c2 = |m (produits) – m (réactifs)| . c2 - Eproduite ≈ 1,00300 x 10– 29 x (299792458)2 - Eproduite ≈ 9,0145 x 10– 13 J |
IX- Exercice 21 page 147. Lois de conservation.
X- Exercice 24 page 148. Quelle énergie !
|
À l’intérieur de la chambre d’expérimentation du Laser Mégajoule (LMJ), les scientifiques de CEA espèrent réaliser une réaction de fusion à l’aide de puissants lasers. Une réaction de fusion envisagée a pour réaction :
- Données : -
Nombre d’Avogadro : NA
= 6,02
x
1023
mol–1 - Masse molaire du carbone : M (C) = 12,0 g / mol
Le pouvoir calorifique moyen du charbon est de 240 kJ / mol. Cela signifie que la combustion complète d’une mole de carbone fournit une énergie égale à 240 kJ. 2)- Réaction de fusion et énergie : a)- Calculer la perte de masse correspondant à la fusion d’un noyau de deutérium et d’un noyau de tritium. b)- Calculer l’énergie libérée par cette réaction. 3)- Calculer l’énergie libérée par la fusion d’une mole de deutérium avec une mole de tritium. 4)- Calculer la masse de charbon qui fournirait la même énergie. |
||||||||||||
|
1)- Réaction de fusion et énergie : a)- Perte de masse : - |Δm| = |m (produits) – m (réactifs)| -
|Δm|
= | m (He) + m (n) –
m (D) – m (T) | -
|Δm|
≈ |6,64466
x 10–
27 + 1,67493
x 10–
27 –
3,34358
x 10–
27– 5,00736
x 10–
27| - |Δm| ≈ 3,1350 x 10– 29 kg b)- Énergie libérée par cette réaction : - Elibérée = |Δm| . c2 = |m (produits) – m (réactifs)| . c2 - Elibérée ≈ 3,1350 x 10– 29 x (299792458)2 - Elibérée ≈ 2,8176 x 10– 12 J 2)- Énergie libérée par la fusion d’une mole de deutérium avec une mole de tritium : - E (mol) = NA . Elibérée -
E (mol) ≈ 6,02
x 1023x
2,8176
x 10–
12 -
E (mol) ≈ 1,70
x 1012 J
/ mol 3)- Masse de charbon nécessaire : - Masse de charbon nécessaire :
-
|
XI- Exercice 30 page 150. L’énergie de liaison des noyaux.
|
La masse d’un noyau est toujours inférieure à la somme des masses des nucléons isolés. La masse manquante |Δm| = |m (noyau) – m (nucléons)| a été convertie en énergie de liaison : Eliaison = |Δm| . c2 Elle correspond à l’énergie qu’il faudrait fournir au noyau pour qu’il soit dissocié en ses nucléons isolés. Pour comparer la stabilité de différents noyaux, il faut comparer les énergies de liaison par nucléon dans le noyau, soit :
1)- Pourquoi la masse du noyau est-elle toujours inférieure à la somme des masses de chacun de ses nucléons isolés ? Comment définit-on l’énergie de liaison ? 2)- Calculer l’énergie de liaison par nucléon de
3)- La comparer à celle de
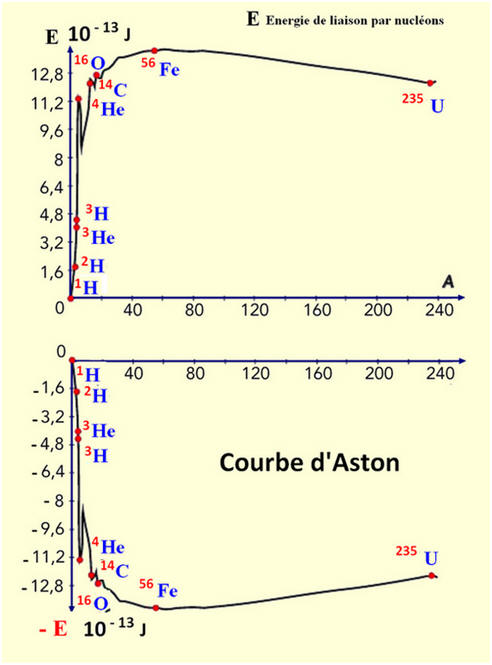
4)- Quel est le noyau le plus stable ? En se servant du document, expliquer pourquoi la fission de l’uranium 235 libère de l’énergie ?
|
||||||||||||||
.
|
1)- La masse du noyau est toujours inférieure à la somme des masses de chacun de ses nucléons isolés : - La masse manquante |Δm| = |m (noyau) – m (nucléons)| a été convertie en énergie de liaison : - Eliaison = |Δm| . c2 - L’énergie de liaison correspond à l’énergie qu’il faudrait fournir au noyau pour qu’il soit dissocié en ses nucléons isolés. - Elle maintient les nucléons entre eux. 2)- Énergie de liaison par nucléon de
- Défaut de masse : - |Δm| = |m (noyau) – m (nucléons)| - |Δm| = |m (noyau) – 6 mp– 8 mn | - |Δm| ≈ |(23,24746 – 6 x 1,67262– 8 x 1,67493) x 10– 27 | - |Δm| ≈ 0,1877 x 10– 27 kg = 1,877 x 10– 28 kg - Énergie de liaison : - Eliaison = |Δm| . c2 - Eliaison ≈ 1,877 x 10– 28 x (299792458)2 - Eliaison ≈ 1,687 x 10– 11 J - Énergie de liaison par nucléon : -
3)- Énergie de liaison par nucléon de
- Défaut de masse : - |Δm| = |m (noyau) – m (nucléons)| - |Δm| = |m (noyau) – 6 mp– 8 mn | - |Δm| ≈ |(92,85851– 26 x 1,67262– 30 x 1,67493) x 10– 27 | - |Δm| ≈ 0,8775 x 10– 27 kg = 8,775 x 10– 28 kg - Énergie de liaison : - Eliaison = |Δm| . c2 - Eliaison ≈ 8,775 x 10– 28 x (299792458)2 - Eliaison ≈ 7,887 x 10– 11 J - Énergie de liaison par nucléon : -
- Comparaison : E (Fe) > E (C) - L’énergie de liaison par nucléon est plus grande pour le noyau de l’atome de fer 56 que pour le noyau de l’atome de carbone 14. 4)- Noyau le plus stable : - Le noyau de l’atome de fer 56 est plus stable que le noyau de l’atome de carbone 14. - Cela est visible sur le graphique. - On préfère tracer la courbe – E = f (A) car ainsi le noyau le plus stable se trouve au fond de la cuvette. - Fission de l’uranium 235 et énergie : - Lors de la fission de l’uranium 235, on obtient deux noyaux plus légers situés à gauche de l’uranium 235 sur la courbe. - Comme on le voit sur le document, les noyaux situés à droite (56 < A < 235) du noyau de l’atome d’uranium 235 sont plus stables. - Lors de la fission, de l’énergie est libérée.
|
|
|
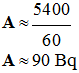
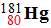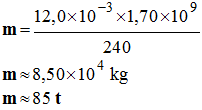
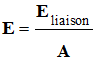