|
Phys. N° 05 |
Radioactivité et réactions nucléaires. Cours. |
|
|
Mots clés : Réaction nucléaire, radioactivité, réactions nucléaires spontanées, réactions nucléaires provoquées, équation d'une réaction nucléaire, lois de conservation, lois de Soddy, énergie libérée, relation Einstein, défaut de masse, énergie de liaison d'un noyau, QCM sur la radioactivité, exercices sur la radioactivité., ... |
|
|
|
II- Équation d’une réaction
nucléaire. |
|
III- Énergie libérée par une
réaction nucléaire. 2)-
une autre unité d’énergie. |
|
Exercices : énoncé avec correction a)- Exercice 7 page 146. Reconnaître des réactions nucléaires provoquées. b)- Exercice 10 page 146. Savoir calculer une activité. c)- Exercice 11 page 146. Utiliser les lois de conservation. d)- Exercice 13 page 146. Écrire une équation de réaction nucléaire. e)- Exercice 14 page 146. Écrire une équation de réaction de fusion. f)- Exercice 15 page 146. Écrire une équation de réaction de fission. g)- Exercice 18 page 147. Histoire et radioactivité. h)- Exercice 20 page 147. De la masse à l’énergie. i)- Exercice 21 page 147. Lois de conservation. j)- Exercice 24 page 148. Quelle énergie ! k)- Exercice 30 page 150. L’énergie de liaison des noyaux. |
I- La réaction nucléaire.
1)- Historique.
La radioactivité a été découverte par Henri Becquerel en 1896 (1852 – 1908).
Il découvre la radioactivité de l’uranium au cours de travaux sur la phosphorescence.
Les travaux sont poursuivis par Pierre et Marie Curie.
En 1898, ils découvrent la radioactivité du polonium Polonium 210 et du radium Radium 226.
En 1903 : prix Nobel de physique (Henri Becquerel avec Pierre et Marie Curie).
On connaît actuellement, une cinquantaine de nucléides naturels radioactifs et environ 1200 nucléides artificiels radioactifs.
2)- Réactions nucléaires spontanées.
a)- Stabilité du noyau et radioactivité.
- La cohésion du noyau est due à l’existence d’une interaction forte, attractive qui unit l’ensemble des nucléons et qui prédomine devant l’interaction électrique (répulsion entre les protons).
- Il y a antagonisme entre l’interaction forte et la répulsion des protons.
- Dans certains cas la cohésion n’est pas suffisante, on dit que les noyaux sont instables.
- Ils se désintègrent spontanément, on dit qu’ils sont radioactifs. Ce sont des radionucléides.
b)- Désintégration radioactive.
-
Une source radioactive peut émettre :
-
Des particules
-
Un rayonnement γ.
-
Les particules émises sont de trois types : les
particules α, β+et β–.
- Ce sont des particules positives, des noyaux d’hélium dont l’écriture symbolique : ion He2+.
- Ces particules sont éjectées à grande vitesse v ≈ 2 × 107 m / s. Ce ne sont pas des particules relativistes.
- Les particules sont directement ionisantes mais peu pénétrantes.
- Elles sont arrêtées par une feuille de papier et par une épaisseur de quelques centimètres d’air.
- elles pénètrent la peau sur une épaisseur de l’ordre de quelques micromètres.
- Elles ne sont pas dangereuses pour la peau.
- Par contre, elles sont dangereuses par absorption interne : inhalation, ingestion.
► Les particules β (bêta).
- On distingue :
-
Les particules β– qui sont des
électrons :
-
Masse : me = 9,1
x 10 – 31 kg
-
Charge : - e = – 1,60
x 10– 19 C.
-
Les particules β+ qui sont des positons
(antiparticule de l’électron).
-
Masse : me = 9,1 x 10 – 31
kg
-
Charge : e = 1,60 x 10 – 19 C.
- Les particules sont émises à grande vitesse v ≈ 2,8 x 10 8 m / s.
- Ce sont des particules relativistes (leur vitesse est voisine de celle de la lumière).
- Elles sont plus pénétrantes mais moins ionisantes que les particules α.
- Elles sont arrêtées par un écran de Plexiglas ou par une plaque d’aluminium de quelques centimètres.
- Elles pénètrent la peau sur une épaisseur de quelques millimètres.
- Elles sont dangereuses pour la peau.
-
Il accompagne l’émission de particules α, β+et
β–.
-
Il est constitué d’une
onde électromagnétique de très courte longueur d’onde (λ
≈ 10 – 12 m et ν ≈ 10
20 Hz).
-
Le rayonnement est
constitué de photons qui se déplacent à la vitesse de la lumière
et dont la masse est nulle.
-
Ils ne sont pas
directement ionisants, mais ils sont très pénétrants.
-
Ils peuvent traverser
jusqu’à 20 cm de plomb.
-
Par interaction avec
les atomes des substances traversées, ils peuvent donner
naissance à des électrons qui eux sont ionisants.
![]() Conclusion :
Conclusion :
- Au cours d’une désintégration radioactive, un noyau père se désintègre spontanément en émettant :
- Un noyau fils,
- Une particule, α, β+ou β–,
- Et un rayonnement électromagnétique γ.
c)- Diagramme de stabilité.
- L’ensemble des noyaux stables (en rouge) forme sur la représentation graphique la vallée de stabilité.
- Les noyaux légers stables ont une tendance à la symétrie.
- Ils se répartissent au voisinage de la première bissectrice (N = Z autant de protons que de neutrons).
- Les noyaux lourds stables s’écartent de la bissectrice. Ils ont plus de neutrons que de protons.
- Pour les noyaux instables :
- En bout de la vallée de stabilité, ils se désintègrent en émettant des particules alpha : ils sont radioactifs alpha.
- Au-dessus de la vallée de stabilité, ils sont émetteur β–. Au-dessous du domaine de stabilité, ils sont émetteurs β+.
► Tableau réduit :
d)- Activité d’un échantillon radioactif.
- L’activité A d’un échantillon radioactif à la date t est le nombre de désintégrations par seconde de cet échantillon.
- L’activité A d’un échantillon radioactif diminue au cours du temps.
- Cette diminution est caractéristique du noyau radioactif présent dans l’échantillon.
- L’unité d’activité est le Becquerel Bq en hommage à Henri Becquerel.
- 1 Bq = 1 désintégration par seconde.
- L’activité d’un échantillon radioactif se mesure à l’aide d’un compteur Geiger.
- Ordre de grandeur des activités :
- L’eau de mer a une activité de l’ordre de 10 Bq par litre.
- Le Radon, présent dans l’air, à l’état de trace, a une activité de quelques centaines de Bq.
- Le corps humain est radioactif. La radioactivité naturelle d’un homme est d’environ 100 Bq / kg.
- Pour un homme de 60 kg, elle est environ de 6000 Bq.
- Les sources radioactives, utilisées au laboratoire, ont une activité comprise entre 4 × 104 Bq et 4 × 107 Bq.
- L’activité d’un gramme de radium est supérieure à 1010 Bq.
- Le becquerel est une toute petite unité de radioactivité.
- On utilise aussi le curie comme unité de radioactivité : 1 Ci = 3,7 × 10 10 Bq.
- L’activité du Césium 137 est de l’ordre de 3 × 10 5 Bq.
► Activité de quelques objets.
|
Sources radioactives |
Eau minérale |
Lait |
Corps humain |
Poisson |
Engrais phosphaté |
Granite |
Plutonium |
|
masse |
1,0 kg |
1,0 kg |
60 kg |
1 kg |
1 kg |
1 kg |
1 kg |
|
Activité |
10 Bq |
240 Bq |
6000 Bq |
100 Bq |
2000 Bq |
8000 Bq |
2 x 1012 Bq |
► Un extrait de texte à méditer :
- La Pomme et l’atome (Douze histoires de physique contemporaine) Sébastien BALIBAR édition Odile Jacob Sciences.
- Extrait :
«



 »
»
3)- Réactions nucléaires provoquées.
a)- Historique.
- La radioactivité artificielle fut mise en évidence en 1934 par Irène et Frédéric Joliot– Curie.
- Ils ont créé par réaction nucléaire un isotope radioactif du phosphore.
- Ils bombardent une feuille d’aluminium avec des particules α produites par du polonium 210.
-
Ils ont réalisé une transmutation (α, n)
produisant du phosphore 30 radioactif.
-
Le phosphore 30 obtenu est émetteur β+.
b)- La fission de noyaux lourds.
- La réaction de fission est une réaction nucléaire provoquée.
- Au cours d’une fission nucléaire, un neutron lent (neutron thermique) brise un noyau lourd fissile en deux noyaux légers.
- Cette réaction libère de l’énergie.
- Les noyaux lourds fissiles utilisés sont l’uranium 235 et le plutonium 239.
- Un neutron lent que l’on appelle aussi neutron thermique a une énergie cinétique : EC < 0,10 eV.
- Remarque : Les noyaux formés par fission sont généralement radioactifs.
- Il existe un très grand nombre de fissions différentes.
- La réaction nucléaire produit de la chaleur.
- Dans une centrale nucléaire, l’énergie thermique est transportée par le fluide caloporteur à travers le circuit primaire.
- Cette énergie thermique est ensuite transformée en énergie électrique par un alternateur.
c)- La fusion de noyaux légers.
- Au cours d’une fusion nucléaire, deux noyaux légers s’unissent pour former un noyau lourd.
- C’est une réaction nucléaire provoquée qui libère de l’énergie.
- Des particules et un rayonnement électromagnétique γ sont émis.
- La fusion contrôlée est réalisée dans des appareils appelés TOKAMAKS (russe tok qui veut dire courant et mak pour magnétisme).
- Il faut porter la matière à une température de l’ordre de107 K et donner une énergie cinétique aux particules EC ≈ 0,10 MeV.
- Dans ces conditions, la matière est à l’état plasma (quatrième état de la matière ; noyaux et électrons ne sont plus liés entre eux).
- Le problème est d’arriver à réaliser le confinement du plasma pendant une durée d’une seconde environ.
-
De nombreux laboratoires étudient la fusion de deux
isotopes de l’hydrogène, le deutérium
 et le tritium
et le tritium
 .
.
- Exemples : Projet ITER, Laser Mégajoule,…
II- Équation d’une réaction nucléaire.
1)- Lois de conservation : Lois de SODDY.
- Toutes les réactions nucléaires vérifient les lois de conservation suivantes :
- Conservation de la charge électrique.
- Conservation du nombre total de nucléons.
- Conservation de la quantité de mouvement.
- Conservation de l’énergie.

- Lois de Soddy :
- Conservation du nombre de masse : A = A’ + a
-
Conservation de la charge :
Z = Z’ + z
- Remarque :
- Lors d’une réaction nucléaire, il n’y a pas conservation des éléments chimiques.
- Dans les équations de réactions nucléaires, on écrit uniquement les particules possédant une charge ou une masse.
- Les rayonnements gamma n’apparaissent pas.
2)- Applications.
a)- Cas d’une réaction spontanée :
►
Radioactivité α : ![]()
-
Un noyau lourd instable éjecte une particule α
(noyau d'hélium
 ) et
donne un noyau fils plus léger, généralement dans un état excité
) et
donne un noyau fils plus léger, généralement dans un état excité
- Exercice 01 : L’uranium 238 est émetteur a. Écrire l’équation de la réaction.

►
Radioactivité β– :
![]()
- Cette radioactivité se manifeste lorsque le noyau présente un excès de neutrons.
- Au cours de la désintégration, il
y a émission d’un électron noté  :
:
- Exercice 02 : le césium 137 est émetteur β–. Écrire l’équation de la réaction.

►
Radioactivité β+ :
![]()
- Cette radioactivité se manifeste lorsque le noyau d’un atome possède trop de protons.
-
Au cours de la désintégration, il y a émission d’un
positon noté
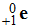 .
.
- Exercice : l’oxygène 14 est émetteur β+. Écrire l’équation de la réaction.
![]()
- Le noyau père possède trop protons :
-

b)- Cas d’une réaction provoquée : fission.
- Exemple :
-
Une fission possible de l’uranium 235, sous l’impact d’un
neutron lent, produit les noyaux
 ,
,
 et
k
neutrons.
et
k
neutrons.
- Écrire l’équation de la réaction. En déduire les valeurs de Z1 et k.
- Réponse :
- remarque : cette réaction fournit plus de neutrons qu’elle n’en consomme.
c)- Cas d’une réaction provoquée : fusion.
- Au cours d’une fusion nucléaire, deux noyaux légers s’unissent pour former un noyau lourd.
- C’est une réaction nucléaire provoquée qui libère de l’énergie.
- Exemple : fusion d’un noyau de deutérium et d’un noyau de tritium.
![]()
► Application :
- L’énergie libérée par fusion nucléaire, appelée énergie thermonucléaire, est à l’origine du rayonnement des étoiles et du Soleil.
- Selon Bethe et Critchfield (1938) l’une des hypothèses possible pour expliquer l’énergie fournie par le Soleil est d’envisager la succession suivante de réactions nucléaires :
-
 (1)
(1)
-
 (2)
(2)
-
 (3)
(3)
-
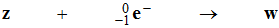 (4)
(4)
-
 (5)
(5)
- x, y, z, w représentent des nucléides.
- Quelles sont les lois utilisées pour équilibrer les réactions nucléaires ? Les équilibrer.
- Montrer que l’on peut remplacer l’ensemble des réactions (1), (2), (3), (4) et (5) par la réaction suivante :
- Nommer et définir ce type de réaction.
- Réponses :
- Lois utilisées : conservation du nombre de nucléons et conservation de la charge globale.
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
- réaction globale :
-

- Il s’agit d’une réaction de fusion nucléaire.
- Des noyaux légers s’unissent et constituent un noyau lourd.
Classification périodique :
III- Énergie libérée par une réaction nucléaire.
1)- Relation d’Einstein.
- Dans la théorie de la relativité restreinte, en 1905, Einstein a montré que la masse est une forme d’énergie.
- Toute particule de masse m, au repos, possède une énergie :
-


- c est une constante universelle, on prend pour valeur celle de la vitesse de la lumière dans le vide :
-
c = 299792458 m / s.
-
Pour les calculs, on peut prendre la valeur approchée :
c = 3,00
× 10 8 m / s.
2)- une autre unité d’énergie.
- Le Joule est une unité d’énergie mal adaptée à l’échelle microscopique.
- A cette échelle, on préfère utiliser l’électron-volt (eV) ou le mégaélectronvolt (MeV)
- Correspondance :
- 1 eV = 1,602189 x 10 –19 J ou 1 MeV = 1,602189 x 10 –13 J
- Remarque : le produit d’une charge par une tension est homogène à une énergie.
3)- Défaut de masse.
- Lors d’une réaction nucléaire, la masse des produits obtenus est inférieure à la masse des réactifs.
- La masse manquante est appelée : perte de masse : on la note |Δm|
- Elle a pour expression :
- |Δm| = |m (produits) – m (réactifs)|
- L’énergie libérée par le système a pour expression :
- Elibérée = |Δm| . c2 = |m (produits) – m (réactifs)| . c2
- Unités :
- L’énergie s’exprime en joule (J)
- La perte de masse |Δm| s’exprime en kilogramme (kg)
- La vitesse de la lumière c s’exprime en m / s.
-
c = 299792458 m / s.
4)- Énergie de liaison d’un noyau.
- La cohésion d’un noyau est due aux interactions fortes entre les nucléons.
- Pour briser un noyau, le milieu extérieur doit fournir de l’énergie.
-
L’énergie de liaison Eℓ
d’un noyau
 est l’énergie
libérée lors de la formation du noyau à partir des nucléons au
repos :
est l’énergie
libérée lors de la formation du noyau à partir des nucléons au
repos :
- Puisque la masse du système diminue, le système libère de l’énergie.
- C’est cette énergie que l’on appelle l’énergie de liaison.
- Eℓ = |Δm| . c2
-

- Avec : |Δm| = |mX – [Z . mp + (A – Z) . mn]|
5)- Application.
- Au cours d’une fusion nucléaire, deux noyaux légers le deutérium et le tritium s’unissent pour former une particule alpha et un neutron.
- C’est une réaction nucléaire provoquée qui libère de l’énergie.
- Écrire l’équation de la réaction.
- Calculer la valeur de la masse des réactifs : m (réactifs).
- Calculer la valeur de la masse des produits : m (produits).
- En déduire la valeur du défaut de masse : |Δm|.
- Calculer la valeur de l’énergie libérée Elibérée lors de cette réaction.
- On fait réagir un mélange de deutérium et de tritium solidifié de masse m = 300 μg.
- Sachant que le mélange est équimolaire, montrer que le nombre de noyaux N de deutérium (ou de tritium) présents est N = 3,59 ´ 1019.
- En déduire l’énergie totale Etot produite par la réaction de fusion.
-
On donne m ( ) = 3,34358
× 10–
27 kg ; m
(
) = 3,34358
× 10–
27 kg ; m
( ) = 5,00736
× 10–
27 kg
) = 5,00736
× 10–
27 kg
-
m ( ) = 1,67493
×10–
27 kg ; m
(
) = 1,67493
×10–
27 kg ; m
( ) = 6,64466
× 10–
27 kg
) = 6,64466
× 10–
27 kg
-
c = 299792458 m / s
- NA = 6,062 x 1023 mol–1
► Réponses :
- Équation de la réaction :
![]()
- Valeur de la masse des réactifs :
-
m (réactifs) = m ( ) +
m (
) +
m ( )
)
-
m (réactifs) ≈ 3,34358
× 10–
27 +
5,00736
× 10–
27
-
m (réactifs) ≈ 8,35094
× 10–
27 kg
- Valeur de la masse des produits :
-
m (produits) = m (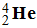 ) + m (
) + m (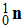 )
)
-
m (produits) ≈ 6,64466
× 10–
27 +
1,67493
× 10–
27
-
m (produits) ≈ 8,31959
× 10
– 27 kg
- Valeur du défaut de masse :
- |Δm| = |m (produits) – m (réactifs)| ≈ |8,31959 × 10– 27 – 8,35094 × 10– 27 |
- |Δm| ≈ 3,135 × 10– 29 kg
- Valeur de l’énergie libérée Elibérée lors de cette réaction :
- Elibérée = |Δm| . c2 = |m (produits) – m (réactifs)| . c2
-
Elibérée ≈ 3,135
× 10–
29 ×
(299792458)2
- Elibérée ≈2,818 × 10– 12 J
- Nombre de noyaux N de deutérium (ou de tritium) présents :
-


-


- Énergie totale Etot produite par la réaction de fusion :
- Etot = N . |ΔE|
- Etot ≈ 3,59 x 1019 x 2,818 x 10– 12
-
Etot ≈ 1,01
x 108 J
6)- Ordre de grandeur d’énergies libérées.
|
Type de réaction |
Fusion |
Fission |
Désintégration alpha |
Combustion du pétrole |
Combustion du charbon |
|
Masse |
1,0 g d’hydrogène fusionné |
1,0 g d’uranium 235 fissionné |
1,0 g de radon désintégré |
1,0 g de pétrole brûlé |
1,0 g de charbon brûlé |
|
Énergie libérée en joule (J) |
3,6 × 1011 |
8,0 × 1010 |
2,0 × 109 |
4,0 × 104 |
2,8 × 104 |
IV- Applications.
1)- QCM : Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).
|
P |
2)- Exercices : Exercices : énoncé avec correction
a)- Exercice 7 page 146. Reconnaître des réactions nucléaires provoquées.
b)- Exercice 10 page 146. Savoir calculer une activité.
c)- Exercice 11 page 146. Utiliser les lois de conservation.
d)- Exercice 13 page 146. Écrire une équation de réaction nucléaire.
e)- Exercice 14 page 146. Écrire une équation de réaction de fusion.
f)- Exercice 15 page 146. Écrire une équation de réaction de fission.
g)- Exercice 18 page 147. Histoire et radioactivité.
h)- Exercice 20 page 147. De la masse à l’énergie.
i)- Exercice 21 page 147. Lois de conservation.
j)- Exercice 24 page 148. Quelle énergie !
k)- Exercice 30 page 150. L’énergie de liaison des noyaux.
|
|



