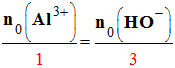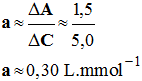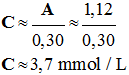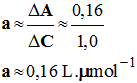|
Changement de couleur et réaction chimique. Exercices. |
|
|
Mots clés : Système chimique, avancement, réaction chimique, tableau d'avancement, avancement maximal, mélange stœchiométrique, absorbance, spectre d'absorption, absorbance en fonction de la longueur d'onde, absorbance en fonction de la concentration, loi de Beer-Lambert, courbe d'étalonnage, ... |
|
|
I- Exercice 6 page 90. Compléter un tableau d’avancement.
|
Les ions cuivre II Cu2+ (aq) réagissent avec les ions hydroxyde HO– (aq) pour former un précipité bleu foncé d’hydroxyde de cuivre II Cu(OH)2 (s).
Compléter le tableau d’avancement ci-dessous en utilisant l’avancement x, l’avancement maximal xmax et les valeurs des quantités initiales.
|
||||||||||||||||||||||||||||
|
Tableau d’avancement :
- On peut déterminer la valeur de l’avancement maximal : -
Avancement
maximal : - Pour déterminer la valeur de l’avancement maximal xmax, on calcule les valeurs de l’avancement qui annulent les quantités de chacun des réactifs. - La plus petite de ces valeurs donne la valeur de l’avancement maximal de la réaction. - Le réactif est l’ion cuivre II Cu2+ (aq) : - 5,0 – xmax1 = 0 Þ xmax1 = 5,0 mol - Le réactif est l’ion hydroxyde HO– (aq) : - 8,0 – 2 xmax2 = 0 Þ xmax2 = 4,0 mol - L’avancement maximal est égal à la plus petite des deux valeurs - xmax = xmax2 = 4,0 mol ≤ xmax1 - En conséquence : - Le réactif limitant est l’ion hydroxyde HO– (aq), il a été totalement consommé. - Le réactif en excès est l’ion cuivre II Cu2+ (aq), il n’a pas totalement réagi.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
II- Exercice 7 page 90. Utiliser un tableau d’avancement.
|
Les ocres du Roussillon sont composées, entre autres, de silice, d’argile et d’un pigment minéral coloré, l’oxyde de fer III de formule brute Fe2O3 (s). Ce solide peut être obtenu en faisant réagir à chaud, du fer métal avec du dioxygène gazeux. L’équation de la réaction est donnée dans le tableau d’avancement ci-dessous.
1)- Quel est le réactif limitant ? 2)- Compléter le tableau en utilisant les valeurs des quantités initiales et les grandeurs x, xmax et n0 (O2). 3)- Il se forme 2,0 mol de Fe2O3 (s). Quelle est la valeur de xmax ? 4)- En déduire la valeur de la quantité de matière initiale n0 (O2). 5)- Quelle est la quantité de fer Fe (s) dans l’état final ? |
||||||||||||||||||||||||||||
|
1)- Réactif limitant : en analysant de tableau d’avancement, on peut affirmer que le réactif limitant est le dioxygène O2 (g) : - Car nf (O2) = 0,0 mol 2)- Tableau d’avancement :
3)- Valeur de xmax : On donne nf (Fe2O3) = 2,0 mol - À la lecture du tableau, on peut en déduire la valeur de xmax : -
nf
(Fe2O3) = 2,0
mol = 2 xmax - xmax ≈ 1,0 mol 4)- Quantité de matière de dioxygène dans l’état initial n0 (O2) = ? - n0 (O2) – 3 xmax = 0 - n0 (O2) = 3 xmax ≈ 3,0 mol 5)- Quantité de matière de fer Fe (s) dans l’état final : - À la lecture du tableau, on peut écrire : -
nf
(Fe) = 10,0 – 4
xmax - nf (Fe) ≈ 10,0 – 4 x 1,0 - nf (Fe) ≈ 6,0 mol - On peut compléter le tableau :
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
III- Exercice 9 page 90. Établir l’état final d’un système (I).
|
En présence d’ions hydroxyde HO– (aq), les ions fer III, Fe3+ (aq), forment un précipité rouille d’hydroxyde de fer III Fe(OH)3 (s). Initialement, 6,0 mmol d’ions fer III, Fe3+ (aq), réagissent avec 12,0 mmol d’ions hydroxyde.
1)- Écrire l’équation de la réaction avec les nombres stœchiométriques entiers les plus petits possibles. 2)- Établir un tableau d’avancement de la réaction. 3)- Calculer la valeur de l’avancement maximal xmax et en déduire le réactif limitant. 4)- Calculer les quantités de matière dans l’état final. |
|
1)- Équation de la réaction :
Fe3+
(aq) +
3 HO–
(aq)
→
Fe(OH)3
(s) 2)- Tableau d’avancement de la réaction :
3)- Valeur de l’avancement maximal xmax et réactif limitant. - Avancement maximal : - Pour déterminer la valeur de l’avancement maximal xmax, on calcule les valeurs de l’avancement qui annulent les quantités de chacun des réactifs. - La plus petite de ces valeurs donne la valeur de l’avancement maximal de la réaction. - Le réactif est l’ion fer III Fe3+ (aq) : - 6,0 – xmax1 = 0 => xmax1 = 6,0 mmol - Le réactif est l’ion hydroxyde HO– (aq) : - 12,0 – 3 xmax2 = 0 => xmax2 = 4,0 mmol - L’avancement maximal est égal à la plus petite des deux - xmax = xmax2 = 4,0 mmol ≤ xmax1 - En conséquence : - Le réactif limitant est l’ion hydroxyde HO– (aq), il a été totalement consommé. - Le réactif en excès est l’ion fer III Fe3+ (aq), il n’a pas totalement réagi. 4)- Les quantités de matière dans l’état final :
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
IV- Exercice 11 page 91. Analyser des graphes.
|
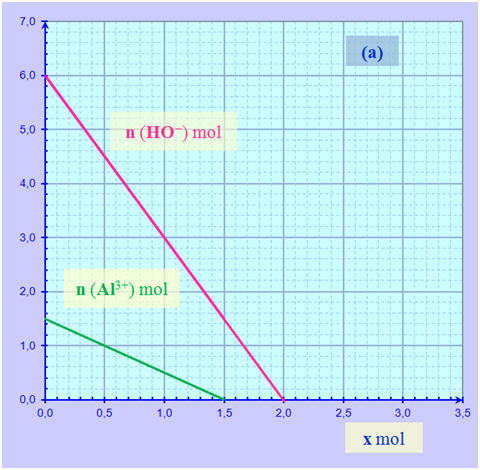
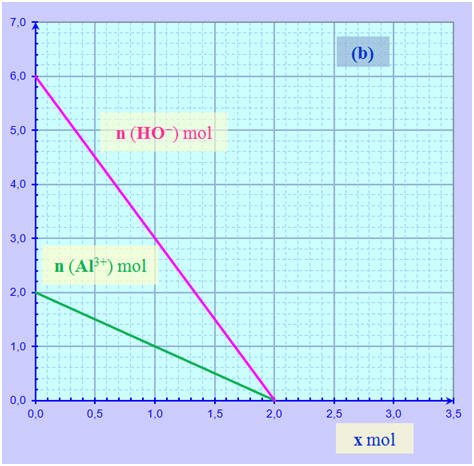
L’hydroxyde d’aluminium Al(OH)3 (s) est un solide blanc qui peut être obtenu lors de la réaction entre les ions aluminium Al3+ (aq) et les ions hydroxyde HO– (aq). L’équation de la réaction est : Al3+ (aq) + 3 HO– (aq) → Al(OH)3 (s) Les graphes (a) et (b) ci-dessous montrent l’évolution des quantités de ces ions en fonction de l’avancement x pour systèmes chimiques différents :
1)- Pour chaque système, déduire des graphes : a)- Les quantités de matière dans l’état initial ; b)- L’avancement maximal ; c)- Le(s) réactif(s) limitant(s). 2)- L’un des deux systèmes correspond-il à un mélange stœchiométrique ? Si oui, lequel ? |
|
1)- Étude de chaque système : Système (a) : a)- Quantités de matière dans l’état initial : - Une lecture graphique permet de déterminer les quantités de matière dans l’état initial : - no (Al3+) ≈ 1,5 mol - no (HO–) ≈ 6,0 mol b)- Avancement maximal : - Les deux droites coupent l’axe horizontal et xmax est égal à la plus petite abscisse
des deux points
d’intersection avec l’axe horizontal.
-
xmax
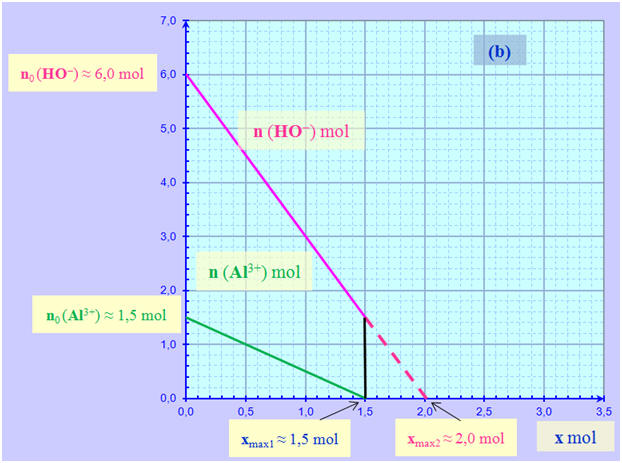
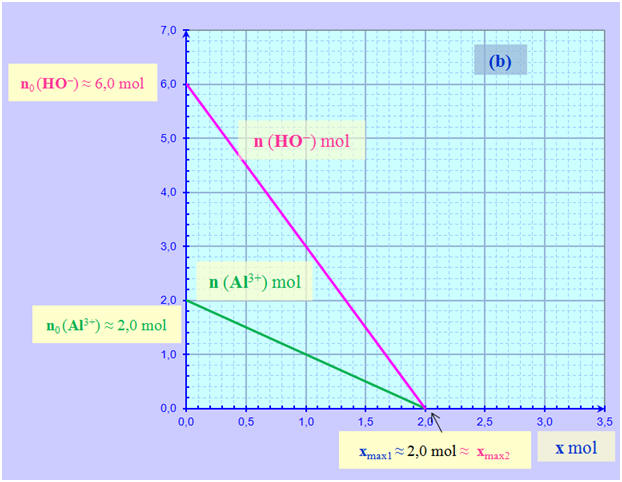
≈ 1,5 mol ≈ xmax1 c)- Le réactif limitant : L’ion aluminium Al3+ (aq) Système (b) : a)- Quantités de matière dans l’état initial : - Une lecture graphique permet de déterminer les quantités de matière dans l’état initial : - no (Al3+) ≈ 2,0 mol - no (HO–) ≈ 6,0 mol b)- Avancement maximal : - Les deux droites coupent l’axe horizontal et xmax est égal à la plus petite abscisse
des deux points
d’intersection avec l’axe horizontal. - Ici les deux droites se coupent sur l’axe horizontal.
-
xmax
≈ 2,0 mol ≈ xmax1 = xmax2 c)- Les réactifs limitants : L’ion aluminium Al3+ (aq) et l’ion hydroxyde HO– (aq). 2)- Mélange stœchiométrique : - Le mélange (b) est un mélange stœchiométrique car en fin de réaction, tous les réactifs ont été consommés. - Les réactifs ont été introduits dans les proportions stœchiométriques.
- Proportions stœchiométriques : -
|
V- Exercice 14 page 91. Tracer une courbe d’étalonnage.
|
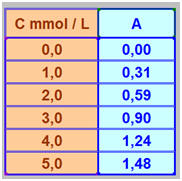
Pour doser par spectrophotométrie une solution jaune de dichromate de potassium [2 K+ (aq) + Cr2O72– (aq)], on a préparé 5 solutions de concentrations C différentes. La mesure de leur absorbance A, pour la longueur d’onde λ = 400 nm, a donné les résultats suivants :
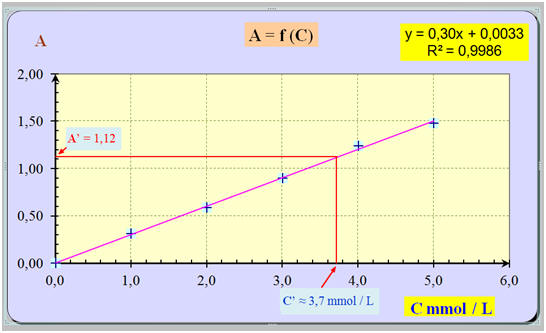
1)- Justifier la valeur de la longueur d’onde λ choisie. 2)- Tracer la courbe d’étalonnage A = f (C). La loi de Beer-Lambert est-elle vérifiée ? 3)- Une solution, de concentration C’ inconnue, a dans les mêmes conditions de mesure, une absorbance A’ = 1,12. En déduire la valeur de la concentration C’. |
|
1)- Choix de la longueur d’onde λ = 400 nm : - Une couleur jaune absorbe majoritairement dans la couleur complémentaire au jaune. - La couleur complémentaire du jaune est la couleur bleue. - La longueur d’onde λ = 400 nm, appartient à une radiation bleue. - Pour réaliser les mesures d’absorbance, le spectrophotomètre est généralement réglé sur la longueur d’onde λmax
correspondant au maximum d’absorption du spectre de
la solution étudiée. - À cette longueur d’onde, la valeur de l’absorbance étant la plus grande, l’incertitude sur la mesure est la plus petite. - On peut déterminer la valeur de λmax à partir de la courbe A = f (λ). 2)- Courbe d’étalonnage A = f (C) et loi de Beer-Lambert : - Tableau de valeurs :
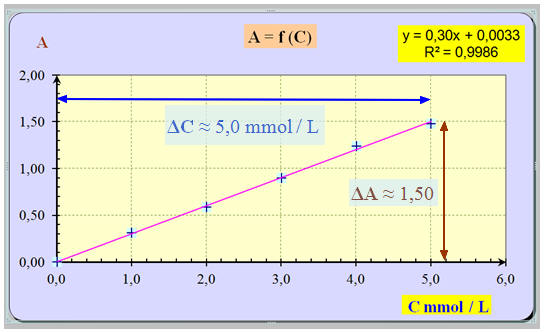
- Graphe : - Les points sont sensiblement alignés. - La droite moyenne obtenue passe par l’origine. - L’absorbance A est proportionnelle à la concentration C de la solution. -
La relation est du
type : A = a . C - La grandeur a étant le coefficient directeur de la droite tracée.
-
Calcul du coefficient
directeur :
ΔA
≈ 1,50 et ΔC
≈ 5,0 mmol / L -
- Relation : A ≈ 0,30 C - L’absorbance A est proportionnelle à la concentration C de la solution en ion dichromate Cr2O72– (aq).
-
A
= k . [Cr2O72–]
avec k = a - La loi de Beer-Lambert est vérifiée. 3)- Valeur de la concentration C’ : - Détermination graphique :
-
A’
= 1,12
-
La lecture graphique
donne C’
≈ 3,7 mmol / L - On peut aussi retrouver cette valeur à l’aide de la relation : -
A ≈ 0,30 C -
|
VI- Exercice 16 page 92. Réaction entre l’acide oxalique et les ions permanganate.
|
Une solution incolore d’acide oxalique, de formule H2C2O4 (aq) est mélangée à une solution violette de permanganate de potassium en milieu acide. La seule espèce colorée du système étudié est l’ion permanganate, MnO4– (aq) de couleur violette. On observe l’évolution suivante :
Initialement, on a mélangé un volume V1 = 20 ,0 mL de solution d’acide oxalique à la concentration C1 = 0,50 mol / L avec un volume V2 = 5,0 mL d’une solution acidifiée de permanganate de potassium de concentration C2 = 0,40 mol / L en ion permanganate. L’acide est en excès et l’eau constitue le solvant de la solution. Le tableau d’avancement de la réaction est donné ci-dessous.
1)- Quel est le réactif limitant ? 2)- Calculer les quantités de matières initiales n1 et n2 en mol. 3)- Compléter littéralement le tableau d’avancement et déterminer le réactif limitant. 4)- Justifier que la couleur finale prise par la solution est cohérente avec la nature du réactif limitant. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
1)- Réactif limitant : - La seule espèce colorée du système étudié est l’ion permanganate, MnO4– (aq) de couleur violette.
- Comme la coloration violette a disparue en fin de réaction, l’ion permanganate a totalement réagi, c’est le réactif limitant. 2)- Quantités de matières initiales n1 et n2 en mol : - Tableau :
3)- Tableau d’avancement : (complété littéralement ) et réactif limitant :
- Réactif limitant : - Avancement maximal : - Pour déterminer la valeur de l’avancement maximal xmax, on calcule les valeurs de l’avancement qui annulent les quantités de chacun des réactifs. - La plus petite de ces valeurs donne la valeur de l’avancement maximal de la réaction. - Le réactif est l’ion permanganate, MnO4– (aq) : - 2,0 x 10 – 3 – 2 xmax1 = 0 => xmax1 ≈ 1,0 x 10 – 3 mol = 1,0 mmol - Le réactif est l’acide oxalique, de formule H2C2O4 (aq) : - 1,0 x 10 – 2 – 5 xmax2 = 0 => xmax2 ≈ 2,0 x 10 – 3 mol = 2,0 mmol - L’avancement maximal est égal à la plus petite des deux valeurs : - xmax = xmax1 ≈ 1,0 x 10 – 3 mol ≤ xmax2 - En conséquence : - Le réactif limitant est l’ion permanganate, MnO4– (aq), il a été totalement consommé. - Le réactif en excès est l’acide oxalique, de formule H2C2O4 (aq), il n’a pas totalement réagi. - Maintenant, on peut compléter le tableau d’avancement : les quantités de matières sont exprimées en mmol.
4)- Couleur finale prise par la solution est cohérente avec la nature du réactif limitant : - La seule espèce colorée du système étudié est l’ion permanganate, MnO4– (aq) de couleur violette. - Comme l’ion permanganate est le réactif limitant, il a totalement réagi, la coloration violette a disparue en fin de réaction. - Ceci est en accord avec l’observation expérimentale de l’état final.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VII- Exercice 18 page 92-93. Étude d’une solution colorée de bain de bouche.
|
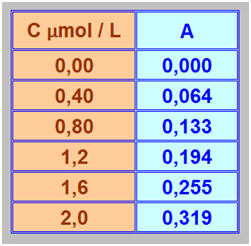
Un spectrophotomètre, réglé sur la longueur d’onde λ = 640 mn, a permis de mesurer l’absorbance de solution en bleu patenté. Les valeurs des concentrations C et de l’absorbance A des solutions sont indiquées dans le tableau ci-dessous :
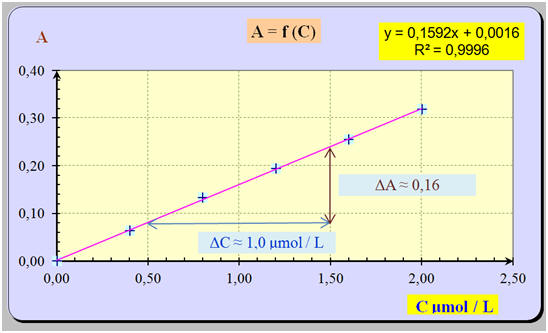
1)- Tracer la courbe d’étalonnage A = f (C). 2)- La loi de Beer-Lambert est-elle vérifiée ? L’Alodont est une solution pour bain de bouche dont la couleur bleue est due à la présence du colorant bleu patenté. L’absorbance de la solution d’Alodont est, dans les mêmes conditions A (Adolont) = 0,126. 3)- En déduire la concentration C (Alodont) en bleu patenté de la solution. 4)- Le spectre d’absorption d’une solution de bleu patenté est donné ci-dessous. Justifier le choix de la longueur d’onde λ = 640 nm. |
|
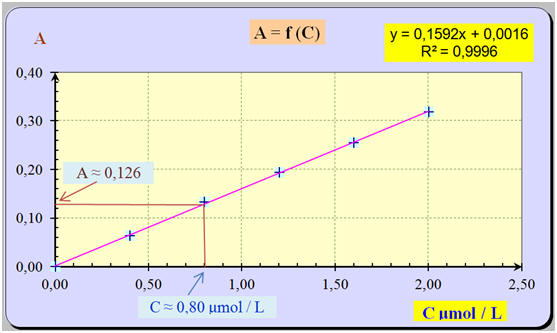
1)- Courbe d’étalonnage A = f (C) : - Tableau de valeurs :
- Graphe et exploitation : - Les points sont sensiblement alignés. - La droite moyenne obtenue passe par l’origine. - L’absorbance A est proportionnelle à la concentration C de la solution. -
La relation est du
type : A = a . C - La grandeur a étant le coefficient directeur de la droite tracée.
-
Calcul du coefficient
directeur :
ΔA
≈ 0,16 et ΔC
≈ 1,0 μmol / L -
- Relation : A ≈ 0,16 C 2)- Loi de Beer-Lambert. - L’absorbance A est proportionnelle à la concentration C de la solution en bleu patenté.
-
A
= k . C avec k = a - La loi de Beer-Lambert est vérifiée. 3)- Concentration C (Alodont) en bleu patenté de la solution. - Exploitation graphique : - Pour A ≈ 0,126, la lecture graphique donne : C ≈ 0,80 μmol / L
4)- Choix de la longueur d’onde λ = 640 mn : - Exploitation de la courbe :
-
λmax
= 640 mn - Pour réaliser les mesures d’absorbance, le spectrophotomètre est généralement réglé sur la longueur d’onde λmax
correspondant au maximum d’absorption du spectre de
la solution étudiée. - À cette longueur d’onde, la valeur de l’absorbance étant la plus grande, l’incertitude sur la mesure est la plus petite. |
|
|