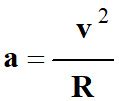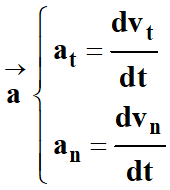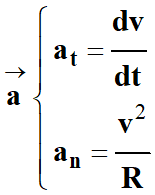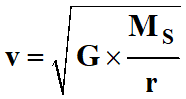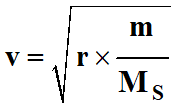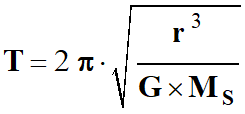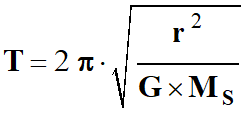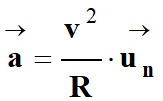QCM N° 13 Mouvement des satellites

QCM N° 13 Mouvement des satellites

QCM. N° 13

Mouvement des satellites.

QCM N° 13 Mouvement des satellites. AIDE Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).
	Énoncé	A	B	C	R
1	Pour appliquer la deuxième loi de Newton au mouvement de la Lune autour de la Terre, le référentiel d’étude adapté est le référentiel :	Géocentrique	héliocentrique	terrestre	A
2	La Terre est en orbite elliptique dans le référentiel :	Géocentrique	héliocentrique	terrestre	B
3	Dans le repère de Frenet, les coordonnées du vecteur vitesse d’un point en mouvement circulaire sont :				B
4	Dans le repère de Frenet, si un point M est en mouvement circulaire selon le cercle de rayon R, les coordonnées de son vecteur accélération sont :				C
5	La période de révolution d’une planète est :	La durée mise par la planète pour faire un tour sur elle-même	La durée mise par la planète pour faire un tour autour du Soleil	La durée d’une journée sur cette planète	B
6	Une planète de masse m en mouvement circulaire uniforme de rayon r autour du Soleil de masse M_S. Sa vitesse est :				A
7	La période de révolution de la planète de masse m en mouvement circulaire uniforme de rayon r autour du Soleil de masse M_S est :				A
8	La période de révolution T d’un système en orbite circulaire de rayon R autour d’un astre attracteur vérifie la relation, avec k une constante :				C
9	Un satellite géostationnaire :	Peut se situer à la verticale au-dessus de Paris	Possède un mouvement circulaire uniforme autour de la Terre	Se situe toujours à 36000 km du centre de la Terre	B
10	L’accélération d’un satellite géostationnaire :	Est nulle	Est constante et inversement proportionnelle au rayon de l’orbite	Varie en fonction de sa position sur l’orbite	B

QCM réalisé avec le logiciel Questy

Pour s’auto-évaluer

Les référentiels :

Les référentiels

- Le référentiel terrestre ou référentiel du laboratoire.

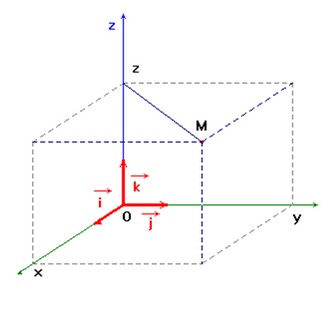
- On utilise, le plus souvent, comme repère lié au référentiel terrestre, deux axes horizontaux et un axe vertical.

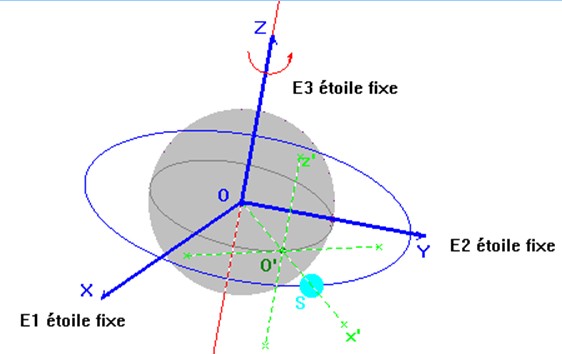
- Le référentiel géocentrique.

- L’origine du repère lié au référentiel Géocentrique est située au centre de la Terre.

- L’axe z’Oz est orienté vers une étoile lointaine : on peut choisir l’étoile polaire.

- Les axes x’Ox et y’Oy sont situés dans le plan équatorial et ils sont orientés vers des étoiles lointaines supposées fixes.

- Ce référentiel est commode pour l’étude des satellites de la Terre.

- Ce référentiel n’est pas entraîné dans le mouvement de rotation de la Terre.

- Dans ce référentiel, la Terre est animée d’un mouvement de rotation uniforme de l’ouest vers l’est, autour de l’axe des pôles

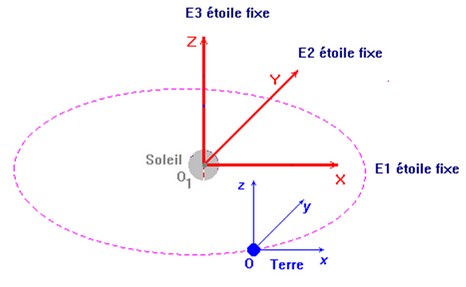
- Le référentiel héliocentrique ou de Copernic.

- L’origine du repère lié au référentiel Héliocentrique est située au centre du Soleil.

- Les axes z’Oz, x’Ox et y’Oy sont orthogonaux et ils sont orientés vers des étoiles lointaines supposées fixes.

- Ce référentiel est commode pour l’étude des satellites du Soleil.

- Dans ce référentiel, la Terre décrit une orbite elliptique autour du Soleil en une année.

- Le référentiel géocentrique est le référentiel le mieux adapté pour étudier le mouvement des satellites de la Terre.

Repère de Frenet :

- Ce repère est bien utile pour l’étude des mouvements circulaires (uniformes)

- Pour simplifier l’étude d’un tel mouvement et en déduire les caractéristiques, il faut utiliser le repère de Frenet :

- repère de Frenet

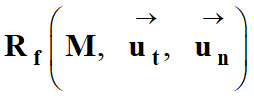
- : désigne un vecteur unitaire tangent à la trajectoire et orienté dans le sens du mouvement.

- : désigne un vecteur unitaire perpendiculaire à et orienté vers le centre O du cercle.

mouvement circulaire

- Le vecteur vitesse est tangent à la trajectoire au point considéré .

- Le vecteur vitesse change de direction à chaque instant.

- Le vecteur accélération peut se décomposer de la façon suivante :

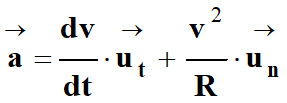
- vecteur accélération

- En conséquence, le vecteur accélération peut être décomposé en une :

- Accélération tangentielle qui dépend de la variation de la valeur de la vitesse :

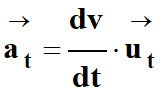- accélération tangentielle avec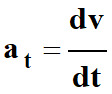

- Accélération normale qui est liée à la variation de la direction du vecteur vitesse.

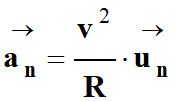- accélération normale avec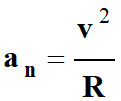

Période de révolution :

- La période de révolution d’une planète du système solaire est la durée qu’elle met pour effectuer un tour autour du Soleil :

- période de révolution

Expression de la vitesse d’une planète du système solaire :

- Une recherche rapide.

- La planète de masse m est soumise à la force exercée par le Soleil.

- Expression de cette force :

-

- Comme le mouvement de la planète est circulaire uniforme :

- L’accélération est normale :

-

- La deuxième loi de Newton permet d’écrire :

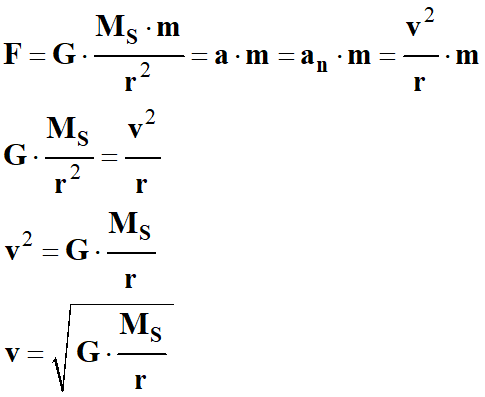
- vitesse v

Troisième loi de Kepler : Loi des périodes.

- Pour toutes les planètes, le rapport entre le cube du demi-grand axe a de la trajectoire et le carré de la période T de révolution est la même : .

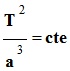- Cette constante ne dépend pas de la masse de la planète.

- Si la trajectoire est un cercle de rayon r, on peut écrire que :.

- Cette constante peut être calculée.

- Dans le cas d’une planète du système solaire :

- La constante s’identifie à relation : constante

- En conséquence, on peut déterminer la masse du Soleil à partir de la période de révolution T et du rayon r de l’orbite d’une planète à trajectoire circulaire.

- Mesure de la constante de gravitation par Cavendish (1798)

Les satellites géostationnaires :

- Un Satellite Géostationnaire est un satellite qui reste toujours à la verticale d’un même point P de la Terre.

- Le plan de l’orbite dans le référentiel géocentrique est le plan équatorial.

- « Ces satellites sont positionnés à la verticale d’un point de l’équateur et sont immobiles par rapport à la surface de la Terre ».

- Un satellite géostationnaire est immobile dans un référentiel terrestre.

- C’est pour cette raison que l’on peut pointer une antenne dans sa direction.

- Un satellite géostationnaire est animé d’un mouvement circulaire dans le référentiel géocentrique.

► Période de révolution T d’un Satellite Géostationnaire :

- Le satellite géostationnaire met la même durée que celle mise par la Terre pour effectuer un tour autour de l’axe des pôles

- C’est la durée pour effectuer un tour dans le référentiel géocentrique :

- C’est la durée d’un jour sidéral

- 1 j = 86164 s = 23 h 56 min 4 s

► Altitude de révolution h d’un Satellite Géostationnaire :

- Schéma de la situation :

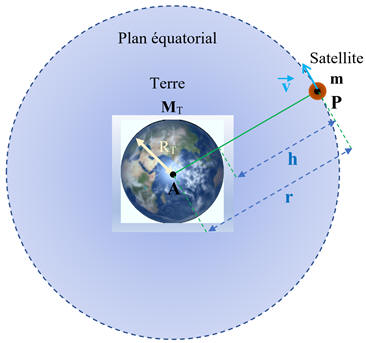
schéma

Accélération du satellite géostationnaire :

- Le vecteur accélération est centripète et sa valeur a est constante.

- a = v² / R

Mouvement	Circulaire uniforme
Vecteur vitesse	Direction : variable et tangente à la trajectoire
	Sens : celui du mouvement
	Valeur : v = constante
	Unité : m . s^–1
Vecteur accélération :	Direction : variable et perpendiculaire à la trajectoire
	Sens : vers le centre de la trajectoire
	Valeur :
	Unités : v : m . s^–1 ; R : m et a : m . s^–2