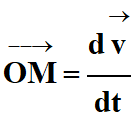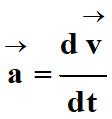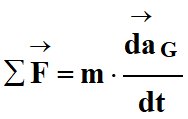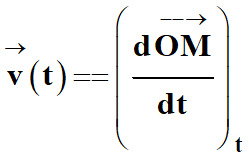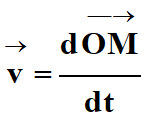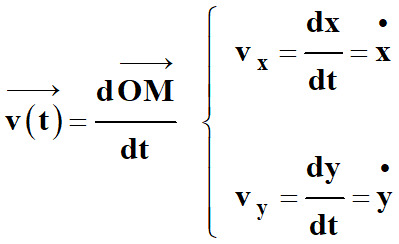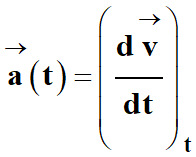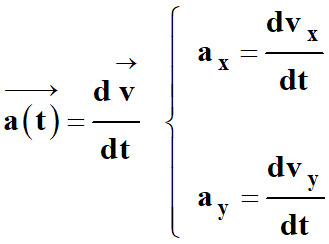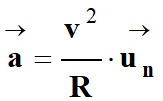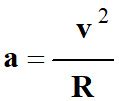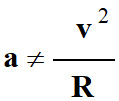|
Mouvements, forces et deuxième loi de Newton |
|
|
|
|
|
|
QCM N° 11
Mouvements, forces
Pour chaque question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
Un référentiel
possède : |
Uniquement
un repère
d’espace |
Uniquement
un repère
de temps |
Un repère
d’espace
et un repère
de temps |
C |
|
2 |
Le vecteur
position est : |
|
|
Repéré par
ses
coordonnées
x
et y |
AC |
|
3 |
La position du
point M est décrite par
les coordonnées de son vecteur
position : x
(t) = t2 – t + 1 y
(t) = 3 t z
(t) = 25. On peut affirmer
que : |
vx
(t) = 0 |
vy
(t) = 0 |
vz
(t) = 0 |
C |
|
4 |
Le vecteur
accélération
est : |
La variation
du vecteur
vitesse sur
une durée
courte |
|
La dérivée
par rapport
au temps
du vecteur
vitesse. |
ABC |
|
5 |
Un point en
mouvement rectiligne
uniforme a : |
Un vecteur
vitesse et un vecteur
accélération
nuls |
Un vecteur
vitesse et un
vecteur accélération
constants
et non nuls |
Un vecteur
vitesse constant
et non nul
et un
vecteur
accélération
nul |
C |
|
6 |
Un passager est
assis dans un bus qui
se déplace à
vitesse constante en
ligne droite. Son mouvement
est : |
Rectiligne
uniforme
dans le
référentiel bus |
Rectiligne
uniforme
dans le référentiel
terrestre |
Rectiligne
uniforme
dans le référentiel
géocentrique |
B |
|
7 |
Le mouvement
d’un point M
est circulaire uniforme,
alors : |
sont
perpendiculaires |
v
est constante |
Vecteur
constant |
A B |
|
8 |
Quelle formule
correspond à l’accélération
d’un mobile en
mouvement circulaire
uniforme |
a
= R / v |
a
= v2 / R |
a
= R2 / v |
B |
|
9 |
Le mouvement
d’un point M
est circulaire non uniforme,
alors : |
Dans le repère
de Frenet :
an
= 0 et
at
= dv / dt |
Le vecteur
accélération est centripète |
Dans le repère
de Frenet :
an
= v2 / R et
at
= dv / dt |
C |
|
10 |
Dans un
référentiel galiléen, la deuxième loi
de Newton s’exprime par :
|
|
|
|
C |
QCM réalisé avec le logiciel Questy
Pour s’auto-évaluer
Un référentiel :
-
Un référentiel est un solide par rapport auquel
on étudie le mouvement d'un mobile ou système.
-
Lors d’une étude de mouvement, il faut toujours
indiquer l’objet dont on étudie le mouvement et aussi l’objet par rapport auquel
on étudie le mouvement.
-
Pour déterminer les
positions successives du système au cours du temps, il faut choisir :
-
Un repère d’espace lié
à l’objet de référence c’est-à-dire au référentiel d’étude,
-
Un repère de temps lié
à une horloge (chronomètre).
-
L’association du
repère d’espace et du repère de temps constitue le référentiel.
Le vecteur position :
-
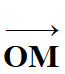
-
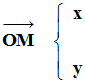
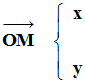
- 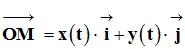
-
x
(t)
et y (t) , ou plus simplement
x et y, sont les
coordonnées du point M à l’instant
t.
-
Unités : les coordonnées,
x et
y s’expriment en mètres (m).
-
Les expressions x (t) et y (t)
sont appelées les équations horaires du mouvement.
Vecteur vitesse :
-
Dans un référentiel
R donné, le vecteur vitesse
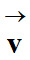 , d’un point
M à l’instant t, est égal
à la dérivée, par rapport au temps, du vecteur position
, d’un point
M à l’instant t, est égal
à la dérivée, par rapport au temps, du vecteur position
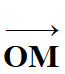 à cet instant :
à cet instant :
|
|
Ou plus simplement
|
|
|
Valeur en mètre (m) |
|
dt |
Valeur en seconde (s) |
|
|
Valeur en mètre par seconde (m . s–1) |
-
Pour connaître les coordonnées du vecteur
vitesse, on dérive le vecteur position par rapport au temps :
|
|
|
|
|
Valeur du vecteur vitesse :
|
-
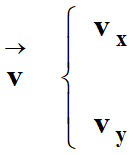
En conséquence :
|
Vecteur position |
par rapport
au temps |
Vecteur vitesse |
|
|
|
-
Le vecteur vitesse traduit les variations du
vecteur position.
-
Dans le cas présent :
vx (t) = 2
t – 1 ;
vy (t) = 3 et
vz (t) = 0
Vecteur accélération :
-
Dans un référentiel
R donné, le vecteur accélération
 d’un point
M à l’instant t, est égal
à la dérivée , par rapport au temps, du vecteur vitesse
d’un point
M à l’instant t, est égal
à la dérivée , par rapport au temps, du vecteur vitesse
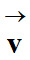 à cet instant :
à cet instant :
|
|
Ou plus simplement
|
|
|
Valeur en mètre (m . s–1) |
|
dt |
Valeur en seconde (s) |
|
|
Valeur en
mètre par seconde au carré (m . s–2) |
|
Vecteur vitesse |
par rapport
au temps |
Vecteur accélération |
|
|
|
-
Le vecteur accélération traduit les variations du
vecteur vitesse.
Mouvement rectiligne uniforme :
-
Un point mobile M est animé d’un mouvement
rectiligne si sa trajectoire est une portion de droite.
|
|
Vecteur
position |
Vecteur
vitesse |
Vecteur
accélération |
|
|
|
|
|
|
Équations
horaires |
x
(t) = v0x . t + x0 |
vx
(t) = v0x |
ax
(t) = 0 |
-
Chronophotographie du mouvement :
-
Représentation graphique de la coordonnée x
de la position en fonction du temps :
-
Représentation graphique de la coordonnée vx
de la vitesse en fonction du temps :
-
Représentation graphique de l’accélération ax
en fonction du temps :
Caractère relatif du mouvement :
-
Le mouvement d’un système dépend du référentiel
d’étude.
Mouvement circulaire uniforme :
-
Dans un référentiel donné, un système est animé
d’un mouvement circulaire uniforme si sa trajectoire est une portion de cercle
de rayon R et si la valeur de sa vitesse v est constante.
-
Repère de Frenet.
-
Pour simplifier l’étude d’un tel mouvement et en
déduire les caractéristiques, il faut utiliser le repère de Frenet :
-
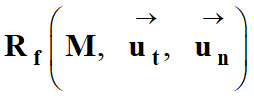
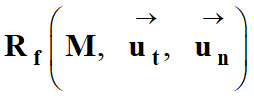
-
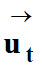 :
désigne un vecteur
unitaire tangent à la trajectoire et orienté dans le sens du mouvement.
:
désigne un vecteur
unitaire tangent à la trajectoire et orienté dans le sens du mouvement.
-
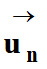 : désigne un vecteur
unitaire perpendiculaire à
: désigne un vecteur
unitaire perpendiculaire à
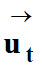 et orienté vers le centre
O du cercle.
et orienté vers le centre
O du cercle.

-
Le vecteur vitesse est tangent à la trajectoire
au point considéré
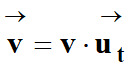 .
.
-
Le vecteur vitesse change de direction à chaque
instant.
-
Le vecteur accélération peut se décomposer de la
façon suivante :
-
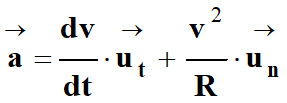
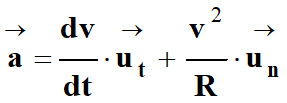
-
En conséquence, le vecteur accélération peut être
décomposé en une :
-
Accélération tangentielle
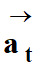 qui dépend
de la variation de la valeur de la vitesse :
qui dépend
de la variation de la valeur de la vitesse :
-
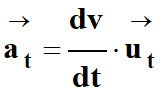 avec
avec
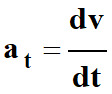
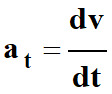
-
Accélération normale
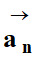 qui est
liée à la variation de la direction du vecteur vitesse.
qui est
liée à la variation de la direction du vecteur vitesse.
-
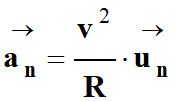 avec
avec
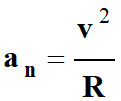
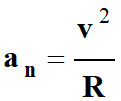
►
Récapitulatif : pour un mouvement circulaire
uniforme
|
Mouvement |
Circulaire uniforme |
|
Vecteur vitesse
|
Direction :
variable et tangente à la trajectoire |
|
Sens : celui du mouvement |
|
|
Valeur : v = constante |
|
|
Unité : m . s–1 |
|
|
Vecteur accélération :
|
Direction :
variable et perpendiculaire à la trajectoire |
|
Sens : vers le centre de la trajectoire |
|
|
Valeur : |
|
|
Unités :
v :
m . s–1 ; R : m et a : m . s–2 |
Les mouvements circulaires non uniformes :
►
Récapitulatif :
|
Mouvement |
Circulaire uniforme non uniforme |
|
Vecteur vitesse
|
Direction :
variable et tangente à la trajectoire |
|
Sens : celui du mouvement |
|
|
Valeur : v = variable |
|
|
Unité : m . s–1 |
|
|
Vecteur accélération :
ou
|
Direction :
variable et non perpendiculaire à la trajectoire |
|
Sens : vers l’intérieur de la trajectoire |
|
|
Valeur :
|
|
|
Unités :
v :
m . s–1 ; R : m et a : m . s–2 |
Énoncé de la deuxième loi de Newton :
|
Dans un référentiel galiléen, la somme des vecteurs
forces
appliquées à un
système S, de masse
m et de centre de masse G,
est égal au
produit de sa masse m par
le vecteur accélération
de son centre de
masse. |
|
|
Valeur des
forces F en newton (N) |
|
Valeur de la
masse m en kilogramme (kg) |
|
|
Valeur de l’accélération aG en mètre par seconde au carré (m
. s–2) |
|
|