QCM réalisé avec le logiciel Questy

Pour s’auto-évaluer

AIDE

Énergie cinétique d’un système :

- L’énergie cinétique est l’énergie que possède un solide du fait de son mouvement.

- Elle dépend de la vitesse et de la masse du solide.

- Pour un solide animé d’un mouvement de translation, tous les points du solide ont à chaque instant la même vitesse que le centre d’inertie du solide :

- L’énergie cinétique E_C d’un système en mouvement de translation est égale au demi-produit de la masse m du solide par le carré de la vitesse v² du système.

- On écrit :

- L’énergie cinétique caractérise un système en mouvement.

- Elle est 

- Proportionnelle à la masse m du solide

- Proportionnelle au carré de la vitesse v du système.

- Elle dépend du référentiel d’étude.

Calcul de la valeur de l’énergie cinétique d’un corps :

-    

-   Les unités : 

Chap N° 14 (Classe de première) : Aspects énergétiques des phénomènes mécaniques

Énergie potentielle de pesanteur :

-  On peut en déduire l’expression de l’énergie potentielle de pesanteur d’un système S de masse m situé à l’altitude y :

-  E_Pp = m . g . y

-  Il existe une origine des altitudes choisie comme référence :

-  De façon générale, on choisit l’origine des altitudes qui simplifie les calculs.

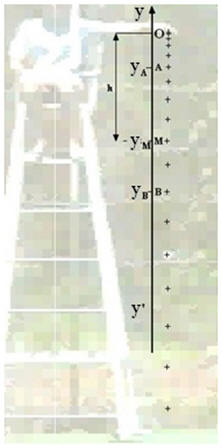
-  À l’altitude y = 0 m , E_P = 0 J.

-  L’axe Oy est orienté vers le haut.

-  L’énergie potentielle est définie à une constante additive près.

-  La différence d’énergie potentielle ne dépend pas du choix de l’origine.

-  Pour les exercices, on choisit l’origine la plus commode, celle qui simplifie les calculs.

-  L’énergie potentielle de pesanteur d’un système de masse m est l’énergie qu’il possède du fait de son interaction avec la Terre.

-  La valeur de cette énergie dépend de la position du système par rapport à la Terre.

Énergie mécanique d’un système.

-  L’énergie mécanique E_m d’un système S de masse m est égale à la somme de son énergie cinétique E_C et de son énergie potentielle E_P.

-  E_m = E_C + E_Pp

-  L’énergie mécanique E_m d’un système S de masse m dépend de la valeur de la vitesse v du système et de sa position dans le référentiel d’étude.

-   

-  La variation de l’énergie mécanique d’un système S en mouvement d’une position A à une position B est égale à la somme des travaux des forces non conservatives  appliquées au système S.

-   

-  Le poids, étant est une force conservative, on lui associe une énergie potentielle de pesanteur E_Pp.

-  Si un système est soumis à son poids et à d’autres forces dont le travail est nul au cours du mouvement, alors l’énergie mécanique de ce système est constante.

Chap N° 11 Mouvement et deuxième loi de Newton

Vecteur position, vecteur vitesse, vecteur accélération :

Le vecteur vitesse :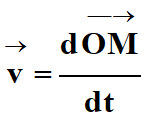  

- Caractéristiques du vecteur vitesse.

- Origine : position occupée par le point mobile à l'instant considéré t.

- Direction : tangente à la trajectoire au point considéré.

- Sens : celui du mouvement à cet instant.

- Valeur : celle de la vitesse instantanée à cet instant.

Définition :

Dans un référentiel R donné, le vecteur vitesse , d’un point M à l’instant t, est égal à la dérivée, par rapport au temps, du vecteur position  à cet instant

►  Représentation du vecteur vitesse.

-  Le vecteur vitesse est tangent à la trajectoire au point considéré.

Les coordonnées du vecteur vitesse :

-  Pour connaître les coordonnées du vecteur vitesse, on dérive le vecteur position par rapport au temps :

Le vecteur accélération :

-  Dans un référentiel R donné, le vecteur accélération d’un point M à l’instant t, est égal à la dérivée , par rapport au temps, du vecteur vitesse  à cet instant :

-  Le vecteur accélération traduit les variations du vecteur vitesse.

Coordonnées du vecteur accélération.

-  Pour connaître les coordonnées du vecteur accélération, on dérive le vecteur vitesse par rapport au temps :

Chap N° 14 (Classe de première) : Aspects énergétiques des phénomènes mécaniques

Travail d’une force constante :

-  Le travail d’une force constante  dont le point d’application M se déplace de la position A à la position B sur le segment [AB]  est égal au produit scalaire du vecteur force  par le vecteur déplacement . On note :

-  Schéma :

Vidéo

-   Application : Calcul du travail d’une force le long du trajet ℓ.

-  Premier chemin :

-  Calculer le travail de la force

-   Sachant que : F = 10,0 N, ℓ = 7,70 cm et α = 30 °.

-   

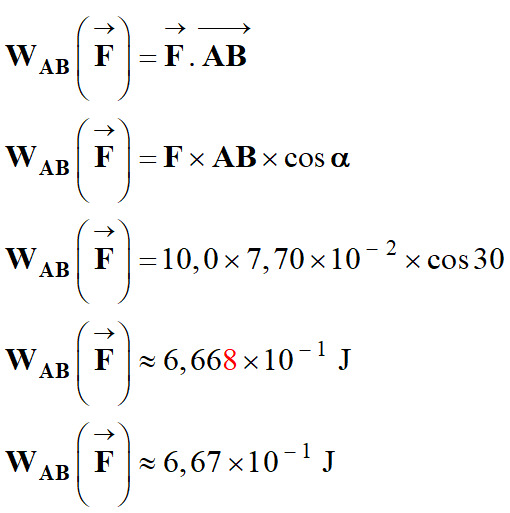
-  Deuxième chemin : ACB

-  Le travail d’une force constante, lors du déplacement de son point d’application M entre A et B ne dépend pas du chemin suivi entre A et B.

-  On est en présence d’une force conservative.

-   Forces conservatives.

-  Une force appliquée à un système S est conservative si son travail ne dépend pas du chemin suivi.

-  Son travail dépend seulement de la position de départ et de la position d’arrivée.

-  Elle ne dépend pas de la trajectoire suivie entre les positions de départ et d’arrivée.

Théorème de l’énergie cinétique :

-  Les unités :

-  Le travail des forces appliquées au système S peut faire varier l’énergie cinétique du système.

-  On dit que le travail mécanique est un mode de transfert de l’énergie.

-  Si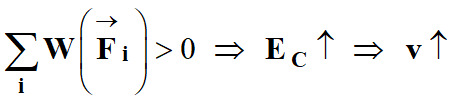

-  Si la somme des travaux des forces appliquées au système est positive, son énergie cinétique augmente et la vitesse du système augmente.

-  Si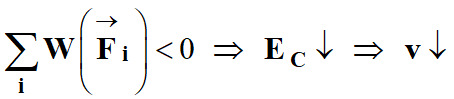

-  Si la somme des travaux des forces appliquées au système est négative, son énergie cinétique diminue et la vitesse du système diminue.

Forces conservatives :

-  Une force appliquée à un système S est conservative si son travail ne dépend pas du chemin suivi.

-  Son travail dépend seulement de la position de départ et de la position d’arrivée.

-  Elle ne dépend pas de la trajectoire suivie entre les positions de départ et d’arrivée.

-  Exemple : travail du poids

-  Ainsi, le poids  est une force conservative.

-  Expression du travail du poids :

-   

-  Le travail du poids pour un déplacement du point A au point B dépend :

-  de l’altitude z_A de l’altitude du point de départ A

-  et de celle de l’altitude z_B du point d’arrivée B.

-  Le poids, étant est une force conservative, on lui associe une énergie potentielle de pesanteur E_P.

-  On considère le système S, de masse m qui se déplace du point A au point B.

-  Représentation schématique :

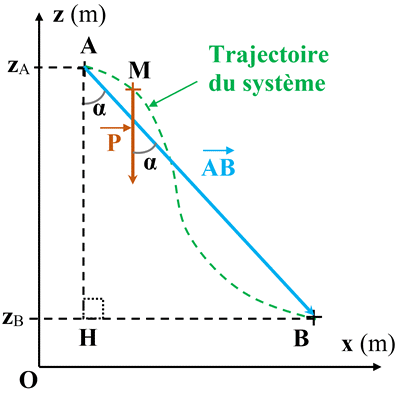
-  Expression de la variation de l’énergie potentielle de pesanteur :

-   

-  D’autre part, on connaît l’expression du travail du poids lors de ce déplacement :

-   

-  On en déduit la relation suivante :

- 

-   

-  Il découle de cette expression :

-  E_PB = m . g . z_B et E_PA = m . g . z_A

-  On peut en déduire l’expression de l’énergie potentielle de pesanteur d’un système S de masse m situé à l’altitude z :

-  E_P = m . g . z

Théorème de l’énergie mécanique :

-  La variation de l’énergie mécanique d’un système S en mouvement d’une position A à une position B est égale à la somme des travaux des forces non conservatives  appliquées au système S.

-   

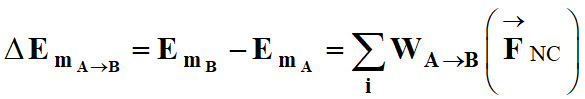
-  Si un système est soumis à son poids et à d’autres forces dont le travail est nul au cours du mouvement, alors l’énergie mécanique de ce système est constante.

Travail d’une force conservative :

-  Si un système est soumis à son poids et à d’autres forces dont le travail est nul au cours du mouvement, alors l’énergie mécanique de ce système est constante.

-  E_m = E_C + E_PP = cte

-  ΔE_m = ΔE_C + ΔE_PP = 0

-  ΔE_C = – ΔE_PP

-  E_C (B) – E_C (A)  = – (E_pp (B) – E_PP (A))

-  E_C (B) – E_C (A)  = E_PP (A) – E_PP (B)

-  Exemple : étude de la chute libre d’une balle de golf :

-  Référentiel d’étude : le sol : référentiel terrestre supposé galiléen.

-  Le système d’étude S : la bille d’acier.

-  Bilan des forces : Le poids  (chute libre)

-  Schéma de la situation :

Deuxième loi de Newton et référentiel galiléen :

-  Un référentiel dans lequel, le centre d’inertie d’un solide, soumis à des forces qui se compensent, est animé d’un mouvement rectiligne uniforme est dit galiléen.

-  Un référentiel galiléen est un référentiel dans lequel le centre d’inertie d’un solide, soumis à des forces qui se compensent, a un mouvement rectiligne uniforme.

-  Un référentiel galiléen est un référentiel dans lequel le principe de l’inertie est vérifié.

- Tout référentiel, animé d’un mouvement rectiligne uniforme par rapport à un référentiel galiléen, est galiléen.

-  Si l’expérience est suffisamment courte, on peut considérer que le référentiel terrestre est galiléen avec une bonne approximation (précision de l’ordre de 10⁻² à 10⁻³)

-  Les lois de Newton ne s’appliquent que si le référentiel utilisé est galiléen.

Deuxième loi de Newton :

-  Autre écriture :

-   

-  L’accélération  est inversement proportionnelle à la masse m du système.