|
Cinématique du point |
|
|
|
|
|
|
QCM N° 10
Cinématique du
point
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
Un référentiel
|
Est lié
à l’objet
d’étude |
Est
nécessairement
immobile |
Est un
corps par
rapport auquel
on étudie le
mouvement
d’autres
objets |
C |
|
2 |
La trajectoire
d’un point |
Est l’ensemble
des positions
successives
occupées par
le point au
cours du temps |
Est une
courbe
qui peut
être une
droite,
un cercle
ou une forme
quelconque |
Est une
succession de
points séparés
par une
distance
toujours
identique |
AB |
|
3 |
Un point est
en
mouvement
rectiligne
si : |
Sa trajectoire
est une droite |
Sa trajectoire
est un cercle |
La norme de
sa vitesse
est constante |
A |
|
4 |
Un point est
en
mouvement
uniforme si : |
Sa trajectoire
est une droite |
Sa trajectoire
est un cercle |
La norme
de sa vitesse
est constante |
C |
|
5 |
Maëlle se
laisse
rouler en
rollers
après avoir
pris
de la vitesse.
Camille court
pour être à
tout
moment à son
niveau.
Yassine
regarde la
situation
sans bouger.
Dans
cette
situation,
Maëlle : |
Est en
mouvement
par rapport
à Camille |
Est en
mouvement
par rapport
à Yassine |
Est en
mouvement
par rapport
à la route |
BC |
|
6 |
Le mouvement
d’un corps : |
Dépend du
référentiel
d’étude |
Est
indépendant
du référentiel
choisi |
Doit toujours
être étudié
dans le
référentiel
terrestre |
A |
|
7 |
On dispose de
la
trajectoire
d’un point. On
s’intéresse à
la
position du
point M
à l’instant
considéré
Le vecteur
vitesse
|
Est tangent à
la trajectoire
au point M |
Est vertical
car
globalement
le point se
dirige vers
le haut |
A la direction
de la flèche
indiquant le
sens du
mouvement |
A |
|
8 |
Le vecteur
vitesse
|
a le sens
du
mouvement |
a comme
norme la
vitesse
instantanée
du point M |
a comme
norme la
vitesse
moyenne
du point
tout au
long du
parcours |
AC |
|
9 |
Le vecteur
vitesse
entre les
instants
t
– Δt et t + Δt
est environ
égal à |
|
|
|
B |
|
10 |
L’expression
de
la variation
du
vecteur
vitesse
t
– Δt et t + Δt est : |
|
|
|
B |
|
11 |
Sur cette
Chronophotographie,
la variation
du vecteur
vitesse
M8
est égale à :
|
|
|
|
A |
|
12 |
Soient les vecteurs
Alors les
coordonnées
de
sont : |
|
|
|
B |
|
13 |
Un système en
mouvement
rectiligne
uniforme a :
|
Un vecteur
vitesse
constant |
Une variation
de vecteur
vitesse
constante
et non nulle |
Une variation
de vecteur
vitesse nulle |
AC |
QCM réalisé avec le logiciel Questy
Pour s’auto-évaluer
Étude d’un système mécanique :
-
Système :
-
Avant de décrire le mouvement d’un objet, il
faut préciser :
-
Le système
S étudié
-
Et le référentiel
R d’étude.
-
l'objet
dont on étudie le mouvement est appelé le mobile
et l'objet de référence est appelé le référentiel.
-
Un
référentiel est un solide
par rapport auquel on étudie le mouvement d'un mobile.
-
Pour décrire le mouvement d'un mobile, il faut
indiquer le référentiel d'étude.
-
Un point matériel représente soit un objet de
petite taille (particule, petite bille), soit un objet de grande taille dont on
néglige les effets de rotation sur lui-même.
-
Généralement, on appelle cet
objet le mobile.
Les référentiels :
-
Le référentiel terrestre ou référentiel du
laboratoire.
-
On utilise, le plus souvent, comme repère lié
au référentiel terrestre, deux axes horizontaux et un axe vertical.
-
Le référentiel géocentrique.
-
L’origine du repère lié au
référentiel Géocentrique est
située au centre de la Terre.
-
L’axe
z’Oz est orienté vers une étoile lointaine : on peut
choisir l’étoile polaire.
-
Les axes
x’Ox et y’Oy
sont situés dans le plan équatorial et ils sont orientés vers des étoiles
lointaines supposées fixes.
-
Ce référentiel est commode pour l’étude des
satellites de la Terre.
-
Ce référentiel n’est pas entraîné dans le
mouvement de rotation de la Terre.
-
Dans ce référentiel, la Terre est animée d’un
mouvement de rotation uniforme de l’ouest vers l’est, autour de l’axe des pôles
-
Le référentiel héliocentrique ou de Copernic.
-
L’origine du repère lié au
référentiel Héliocentrique
est située au centre du Soleil.
-
Les axes
z’Oz, x’Ox
et y’Oy sont orthogonaux et
ils sont orientés vers des étoiles lointaines supposées fixes.
-
Ce référentiel est commode pour l’étude des
satellites du Soleil.
-
Dans ce référentiel, la Terre décrit une
orbite elliptique autour du Soleil en une année.
La trajectoire d’un point mobile :
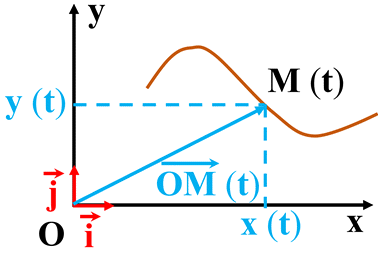
-
Dans un référentiel donné, on
appelle trajectoire d’un point, l’ensemble des positions successives que ce
point occupe au cours de son mouvement.
-
La trajectoire d’un point
mobile dépend du référentiel d’étude.
-
Si la trajectoire est une
droite, le mouvement est rectiligne.
-
Si la trajectoire est un
cercle, le mouvement est circulaire.
-
Si la trajectoire est une
portion de courbe, le mouvement est curviligne.
Les différents types de mouvement rectiligne :
-
Un point est animé d’un
mouvement rectiligne si sa trajectoire est une droite.
-
Mouvement rectiligne
uniforme :
-
Mouvement rectiligne varié :
(il peut être accéléré ou retardé)
Mouvement uniforme :
-
Dans un référentiel donné, un
système est animé d’un mouvement uniforme si la valeur de sa vitesse
v est
constante au cours du mouvement.
-
Le mobile parcourt des
distances égales pendant des durées égales :
-
Chronophotographie d’un
mouvement rectiligne uniforme :
-
Mouvement circulaire
uniforme :
Caractère relatif du mouvement d’un système :
-
Suivant le référentiel
d’étude, un objet dont on étudie le mouvement peut être immobile ou en
mouvement.
-
Le mouvement d’un mobile est
lié au référentiel d’étude.
-
Un objet peut être en
mouvement par rapport à un référentiel et immobile par rapport à un autre
référentiel.
-
Un objet est en mouvement
lorsque sa distance par rapport au référentiel d'étude varie au cours du temps.
-
Pour affirmer qu'un objet est
en mouvement, on choisit un référentiel d'étude, un objet de référence.
Mouvement d’un mobile et référentiel d’étude :
-
Le mouvement d’un mobile est
lié au référentiel d’étude.
-
Lorsque l’on étudie le
mouvement d’un objet, il faut toujours préciser le référentiel d’étude
(mouvement par rapport à)
Le vecteur vitesse :
-
Caractéristiques du vecteur
vitesse.
-
Origine
: position occupée par le point mobile à l'instant
considéré
t.
-
Direction
: tangente à la trajectoire au point considéré.
-
Sens
: celui du mouvement à cet instant.
-
Valeur
: celle de la vitesse instantanée à cet instant.

-
On représente le vecteur
vitesse par un segment fléché.
-
Longueur du représentant
ℓv
:
-
Une échelle de représentation
est indispensable.
-
Elle associe la longueur du
segment fléché à la valeur de la vitesse instantanée.
-
Exemple : 1 cm ↔
0,1 m . s–1.
-
Si
vi
= 0,32 m . s–1
alors ℓvi
= 3,2 cm
Caractéristiques du vecteur vitesse.
-
Origine
: position occupée par le point mobile à l'instant
considéré
t.
-
Direction
: tangente à la trajectoire au point considéré.
-
Sens
: celui du mouvement à cet instant.
-
Valeur
: celle de la vitesse instantanée à cet instant.
Détermination des caractéristiques du vecteur vitesse :
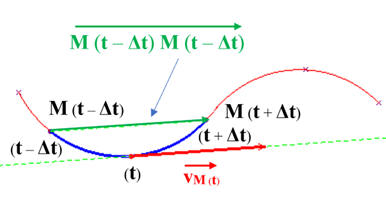
-
Exemple :
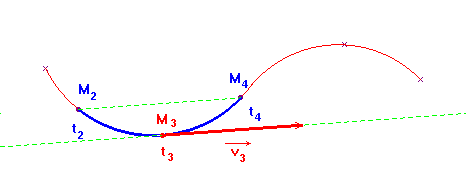
|
On représente le vecteur vitesse
par un segment fléché : -
Vecteur vitesse du point mobile
M
à l'instant t3,
-
Origine :
Position occupée par le point mobile à l'instant
considéré t c'est-à-dire le point M3. -
Direction :
Tangente à la trajectoire au point considéré :
droite parallèle à (M2 M4)
issue de M3. -
Sens : Celui
du mouvement à cet instant -
Valeur : Celle
de la vitesse instantanée à cet instant : -
-
Longueur du
représentant ℓv :
- Une échelle de représentation est indispensable. - Elle associe la
longueur du segment fléché à la valeur de la vitesse
instantanée. - Exemple : 1 cm ↔ 0,1 m / s. - En conséquence si v3 ≈ 0,40 m / s,
-
Le segment fléché
aura une longueur : ℓv3 = 4 cm. |
Vecteur variation du vecteur vitesse :
Cinématique et dynamique newtoniennes. (Cours TS 2010)
-
Lors d’un mouvement, le
vecteur vitesse
![]() d’un
système peut varier en direction, en sens ou en valeur.
d’un
système peut varier en direction, en sens ou en valeur.
-
Le vecteur variation de
vitesse
![]() n’est
alors pas égal au vecteur nul.
n’est
alors pas égal au vecteur nul.
-
Le vecteur variation de
vitesse
![]() d’un
système en mouvement entre deux positions
Mi
et Mj
est défini par :
d’un
système en mouvement entre deux positions
Mi
et Mj
est défini par :
-
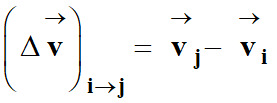
-
Tracé du vecteur variation de
vitesse ![]()
-
L’origine du vecteur est le
point B.
-
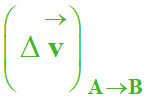
-
Dans le cas de la question
posée : ![]()
-
avec
t1
= t –
Δt et
t2
= t –
Δt
Détermination du vecteur variation du vecteur vitesse :
-
![]()

Coordonnées du vecteur variation du vecteur vitesse :

Mouvement rectiligne uniforme et vecteur vitesse :
-
Mouvement rectiligne :
-
Dans un référentiel donné, un
point mobile
M est animé
d’un mouvement rectiligne si sa trajectoire est une portion de droite.
-
Mouvement uniforme :
-
Dans un référentiel donné, un
système est animé d’un mouvement uniforme si la valeur de sa vitesse
v est
constante au cours du mouvement.
-
Le
vecteur vitesse garde la même direction, le même sens et la même valeur au cours
du temps :
-
![]()
-
![]()
-
Caractéristiques graphiques
du mouvement rectiligne uniforme :
|
|
Vecteur
position |
Vecteur
vitesse |
Vecteur
accélération |
|
|
|
|
|
|
Équations
horaires |
x
(t) = v0x .
t +
x0 |
vx
(t) = v0x
|
ax
(t) = 0 |
Chap N° 11 Mouvement et deuxième loi de Newton
|
|