QCM. N° 03

Dosage par titrage


 
 

 

 

QCM N° 03

Dosage par titrage

AIDE

Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).

 

Énoncé

A

B

C

R

1

On veut préparer un volume

V = 200,0 mL d’une solution

d’hydroxyde de sodium de

concentration apportée

c = 1,00 mol . L–1.

Pour préparer cette solution

par dissolution, il faut utiliser :

 

Donnée : Masse molaire de

l’hydroxyde de sodium :

M = 40,0 g . mol–1

Une fiole

jaugée de

200,0 mL

Une éprouvette

graduée de

200 mL

Une burette

graduée de

200 mL

A

2

On veut préparer un volume

V = 200,0 mL d’une solution

d’hydroxyde de sodium de

concentration apportée

c = 1,00 mol . L–1.

Pour préparer cette solution

par dissolution, il faut peser

une masse d’hydroxyde de

sodium

 

Donnée : Masse molaire de

l’hydroxyde de sodium :

M = 40,0 g . mol–1

m = 8 g

m = 5,00 g

m = 8,00 g

C

3

On veut préparer un volume

V = 200,0 mL d’une solution

d’hydroxyde de sodium de

concentration apportée

c = 1,00 mol . L–1.

Pour préparer cette solution

par dilution d’une solution

mère de concentration

c0 = 20,0 mol . L–1, il faut

prélever un volume de

solution mère :

V’ = 10,0 mL

V’ = 100,0 mL

V’ = 8,0 mL

A

4

La demi-équation du couple

H2O (ℓ) / HO– (aq) est :

H2O (ℓ) + H+

= HO– (aq)

HO– (aq) + H+ 

= H2O (ℓ)

H2O (ℓ)

= HO– (aq) + H+

BC

5

Les couples acide / base

de l’eau sont :

H2O (ℓ) / H3O+ (aq)

Et

H2O (ℓ) / HO– (aq)

H3O+ (aq) / H2O (ℓ)

Et

HO– (aq) / H2O (ℓ)

H3O+ (aq) / H2O (ℓ)

Et

 H2O (ℓ) / HO– (aq)

C

6

Soient les couples

NH4+ (aq) / NH3 (aq)

et H2O (ℓ) / HO– (aq).

On peut envisager

les réactions :

NH4+(aq) + H2O(ℓ)

 =

HO–(aq) + NH3(aq)

NH4+(aq) + HO–(aq)

=

NH3 (aq) + H2O (ℓ)

NH3 (aq) + H2O (ℓ)

=

NH4+(aq) + HO–(aq)

BC

7

On considère une solution

d’hydroxyde de sodium

(Na+ (aq) + HO– (aq))

On mesure la conductance

G = 9,64 × 10–4 S avec une

cellule de constante 90 m–1.

La conductivité est :

1,07 × 10–5

S . m–1

8,68× 10–2

S . m–1

8,68× 10–5

S . m–1

B

8

On considère une solution

d’hydroxyde de sodium

(Na+ (aq) + HO– (aq))

Si la conductivité de la

solution est

σ = 8,68× 10–2 S . m–1,

sa concentration est :

 

 Données : (S.m2.mol–1)

λ (HO–)=19,8×10–3

λ (Na+) = 5,0×10–3

3,50 × 10–3

mol . L–1

3,50

mol . L–1

3,50

mol . m–3

AC

9

On considère une solution

d’hydroxyde de sodium

(Na+ (aq) + HO– (aq))

La conductivité d’une

solution en concentration

apportée

c = 1,00 × 10–2 mol . L–1

est :

 

Données : (S.m2.mol–1)

λ (HO–)=19,8×10–3

λ (Na+) = 5,0×10–3

2,48 × 10–4

S . m–1

2,48 × 10–1

S . m–1

2,48 × 102

S . m–1

B

10

On verse dans un erlenmeyer

un volume VA d’une solution

contenant l’espèce chimique

A de concentration cA.

On y ajoute progressivement

une solution contenant

l’espèce B de concentration

cB connue. L’équation de la

réaction support du titrage est :

3 A + B → C + 2 D

De toutes les espèces,

seule B est colorée.

Le volume équivalent est VE.

Pour ce titrage, A est :

La solution

titrée

Le réactif

titrée

Le réactif

titrant

B

11

On verse dans un erlenmeyer

un volume VA d’une solution

contenant l’espèce chimique

A de concentration cA.

On y ajoute progressivement

une solution contenant

l’espèce B de concentration

cB connue. L’équation de

la réaction support du

titrage est :

3 A + B → C + 2 D

De toutes les espèces, seule

B est colorée.

Le volume équivalent est VE.

La solution contenant B est

initialement placée :

Dans un

erlenmeyer

Dans une

burette

graduée

Sur

agitation

magnétique

B

12

On verse dans un erlenmeyer

un volume VA d’une solution

contenant l’espèce chimique

A de concentration cA.

On y ajoute progressivement

une solution contenant

l’espèce B de concentration

cB connue. L’équation de la

réaction support du titrage est :

3 A + B → C + 2 D

De toutes les espèces,

seule B est colorée.

Le volume équivalent est VE.

L’équivalence est repérée par :

La disparition

de la couleur

de A

La disparition

de la couleur

de B

La persistance

de la couleur

de B

C

13

On verse dans un erlenmeyer

un volume VA d’une solution

contenant l’espèce chimique

A de concentration cA.

On y ajoute progressivement  

une solution contenant

l’espèce B de concentration

cB connue.

L’équation de la réaction

Support du titrage est :

3 A + B → C + 2 D

De toutes les espèces,

seule B est colorée.

Le volume équivalent est VE.

La concentration de A dans

la solution titrée vérifie :

C

haut

QCM réalisé avec le logiciel Questy

Pour s’auto-évaluer

 

AIDE

 

La dissolution :

 

-  La fiole jaugée : V = 200,0 mL
-  Concentration molaire volumique : c = 1,00 mol . L–1
-  Quantité de matière nécessaire :
-  n = c . V => n = 1,00 × 200,0 × 10–3  
-  n ≈ 0,200 mol
-  Masse de soluté nécessaire :
-  m = n . M => m = 0,200 × 40,0
-  m ≈ 8,00 g. Autre résolution :
-  m = n . M = c . V. M = 1,00 × 200,0 × 10–3 × 40,0
-  m ≈ 8,00 g
-  Mode opératoire :

   

-  La fiole jaugée : V = 200,0 mL
-  Concentration molaire volumique : c = 1,00 mol . L–1
-  Quantité de matière nécessaire :
-  n = c . V => n = 1,00 × 200,0 × 10–3  
-  n ≈ 0,200 mol
-  Masse de soluté nécessaire :
-  m = n . M => m = 0,200 × 40,0
-  m ≈ 8,00 g

 

Préparation par dilution :

-  Lors d’une dilution, la concentration molaire du soluté diminue, mais sa quantité de matière ne change pas.
-  On dit qu’au cours d’une dilution, la quantité de matière de soluté se conserve.
-  La solution de départ est appelée la solution mère et la solution diluée est appelée la solution fille.

SM

{

CM = 

Dilution

SF

{

CF = 

VM = ?

→

VF = 

nM  = CM . VM

 

nF  = CF . VF

Solution mère

 nM = nF 

Solution fille

-  si A représente l’espèce présente dans la solution.
-  La quantité de matière nA de cette espèce est la même dans la solution mère et dans la solution fille.
-  Il y a conservation de la quantité de matière de soluté :
-  la quantité de matière de soluté présente dans la solution mère : nA = CM . VM (1)
-  la quantité de matière de soluté présente dans la solution fille  : nA = CF . VF (2)
-  Conséquence : CM . VM = CF . VF (3) avec obligatoirement VM < VF.
-  Avec les notations de l’ énoncé 
-  c0 . V’ = c . V
-   
-  Mode opératoire :

 

 

Couples acide/base : La notation AH / A–

-  L’acide AH et sa base conjuguée A– forment un couple acide-base noté AH / A–.
-  Il est possible de passer d’un à l’autre par transfert d’un ion hydrogène.
-  Écriture de la demi-équation du couple acide-base :

AH (aq)

 

A– (aq)

+

H+

Acide

 

Base

 

ion hydrogène
-  Autrefois, on utilisait le signe =, maintenant, on utilise
-  Signification :
-  Le signe  signifie que le transfert d’ion hydrogène peut se produire dans les deux sens.

AH (aq)

→

A– (aq)

+

H+

Ou bien

A– (aq) + H+

→

AH (aq)

 

 

Espèce amphotère.

-  L’eau appartient à deux couples acido-basiques.
-  L’ion H3O+ est l’acide du couple H3O+ (aq) / H2O (ℓ)
-  L’ion HO– (aq) est la base du couple H2O (ℓ) / HO– (aq).
-  L’eau est la base du couple H3O+ (aq) / H2O (ℓ) et l’acide du couple H2O (ℓ) / HO– (aq).
-  On dit que l’eau est un ampholyte ou une espèce amphotère.
-  On est en présence de deux couples acido-basiques.

Réaction acido-basique :

-  Au cours d’une réaction acide-base, l’acide d’un couple réagit avec la base d’un autre couple.
-  Une réaction acido-basique consiste à un transfert d'un proton entre l’acide A1H d’un couple sur la base A2– d’un autre couple.
-  Couple acide / base 1 : A1H   H + +  A1–
-  Couple acide / base 2  : A2H    H + +  A2–
-  Équation de la réaction :
-  On se place dans le cas où l’acide A1H réagit sur la base A2–

A1H  +  A2–    A1–  +  A2H

Autre cas

A1H  +  A2–  →  A1–  +  A2H

-  L’équation s’écrit avec
-  une double flèche  si la réaction est non totale ;
-  une simple flèche → si la réaction est totale.
-  cette réaction met en jeu les couples acide / base suivants : A1H / A1– et A2H / A2–.

NH3 (aq) + H+

 

NH4+ (aq)

 

 

 

H2O (ℓ)

 

HO– (aq) + H+

 

 

 

NH3 (aq + ) + H2O (ℓ)

 

NH4+ (aq) + HO– (aq)

Autre cas 

NH4+ (aq)

 

NH3 (aq) + H+

 

 

 

HO– (aq) + H+

 

H2O (ℓ)

 

 

 

NH4+ (aq) + HO– (aq)

 

NH3 (aq) + H2O (ℓ)

 

Mesure de la conductance :

 

-  La conductance G d’une portion de solution est proportionnelle au rapport .
-  Par définition, le coefficient de proportionnalité est appelé :
-  Conductivité de la solution ionique que l’on note σ ‘’sigma minuscule’’.
-  On écrit :

 

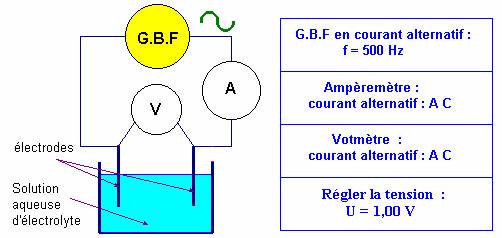
G est la conductance en siemens S

S : surface des électrodes en m2.

ℓ : distance entre les électrodes en m.

σ : conductivité de la solution en S . m– 1  
-  La grandeur σ est caractéristique de la solution.
-  Elle rend compte de la capacité de la solution à conduire le courant électrique.
-  Elle ne dépend pas de la géométrie de la cellule.
-  La grandeur σ est liée à la nature et la concentration des ions présents dans la solution.
-  La conductance G :
-  La conductance G est l’inverse de la résistance R d’une portion de solution.
-  G dépend de la solution et des caractéristiques géométriques de la cellule de mesure.
-  Pour s’affranchir de ces caractéristiques, on définit la conductivité σ à partir de la conductance :
-  G = kcellule . σ
-  La grandeur kcellule est la constante de la cellule.
-  Dans l’énoncé, on donne k = 90 m–1
-  La grandeur k représente le rapport .
-  .
-  Lorsqu’on réalise un dosage avec un conductimètre, on utilise toujours la même cellule.

 

La conductivité et la concentration :

-  La conductivité σ de la solution est égale à la somme des conductivités due aux cations et aux anions.
-  On écrit : σ = σ (+) + σ (–)
-  Formule générale :
-   
-  La conductivité σ d’une solution ionique dépend de la nature des ions présents Xi et de leur concentration [ Xi ] respectives.
-  Exemple : Pour une solution d’hydroxyde de sodium :
-  Solution d’hydroxyde de sodium :

 

eau

 

 

 

NaOH (s)

→

Na+ (aq)

+

HO– (aq)

n

 

0

 

0

0

 

n / V

 

n / V

 

 

C

 

C
-  Or : C = [HO–] = [Na+]
-  σ = λ (HO–) . [ HO– ] + λ (Na+) . [ Na+ ]
-  σ = {λ (HO–) + λ (Na+) } . C
-   
-  Attention aux unités pour les volumes : mètre cube et litre : 1 m3 = 1000 L.
-  Énoncé de la loi de Kohlrausch :

La conductivité σ d’une solution diluée d’une espèce ionique dissoute

est proportionnelle à sa concentration molaire C en soluté apporté :

σ = k . C

 

σ = k . C

C ; concentration en mol . L– 1  

k : coefficient de proportionnalité en S . L .  m– 1. mol– 1  

σ : conductivité de la solution en S . m– 1  
-  À partir de la mesure de la conductivité d’une solution, on peut déterminer la valeur de sa concentration.
-  Courbe σ = f (C) :
-  La courbe obtenue est une droite qui passe par l’origine pour les solutions dont la concentration est inférieure à 2,0 × 10–2 mol . L–1.
-  Exemple : Cas d’une solution aqueuse de diiode.

 

-  On obtient la courbe d’étalonnage.
-  Ce graphe est une portion de droite passant par l’origine.
-  L’absorbance A est proportionnelle à la concentration C de la solution de diiode.
-  A = k . [I2].
-  Remarque : la solution colorée doit être suffisamment diluée, 
-  C ≤ 1,0 × 10–2 mol . L–1, et le spectrophotomètre ne doit pas saturer.
-  Le spectrophotomètre :

 

 Conductivité d’une solution ionique :

-  Solution d’hydroxyde de sodium :

 

eau

 

 

 

NaOH (s)

→

Na+ (aq)

+

HO– (aq)

n

 

0

 

0

0

 

n / V

 

n / V

 

 

C

 

C
-  Or : C = [HO–] = [Na+] = 1,00 × 10–2 mol . L–1 = 1,00 × 10–2 × 1000 mol . m–3
-  1 L = 1 / 1000 m3 
-  C = [HO–] = [Na+] = 10,0 mol . m–3
-  σ = λ (HO–) . [ HO– ] + λ (Na+) . [ Na+ ]
-  σ = {λ (HO–) + λ (Na+) } . C
-  σ = {19,8 × 10–3 + 5,0 × 10–3 } × 1,00 × 10–2 × 1000
-  σ ≈ 2,48 × 10–2 S . m–1
-  Loi de Kohlrausch :
-  La conductivité d’une solution ionique :

La conductivité σ d’une solution diluée d’une espèce ionique

dissoute est proportionnelle à sa concentration molaire C en

soluté apporté :

σ = k . C

 

 

 

σ = k . C

C ; concentration en mol . L– 1  

k : coefficient de proportionnalité en S . L .  m– 1. mol– 1  

σ : conductivité de la solution en S . m– 1  
-  Exemple : À partir des conductivités σ de solutions de différentes concentrations C en chlorure de calcium, on obtient la courbe suivante ;

 

-  La courbe obtenue est une portion de droite passant par l’origine.
-  Traduction physique : σ = a × C
-  σ (mS . cm–1) ≈ 0,270 × C (mmol . L–1) (avec trois chiffres significatifs)
-  Le coefficient de proportionnalité : coefficient directeur de la droite tracée

 

-   
-  À partir de cette courbe d’étalonnage, on peut retrouver la concentration d’une solution de chlorure de calcium !
-  Exemple ; La conductivité de la solution diluée S est :
-  σS = 2,25 mS . cm–1
-  Méthode graphique :

 

-  CS ≈ 8,4 mmol . L–1.

Le conductimètre :

 

Le conductimètre est constitué :

-  D'une sonde de conductimétrie (deux plaques conductrices en vis-à-vis,

alimentées par une tension alternative).

-  D'un boîtier qui sert d'alimentation pour la sonde.

-  Ce boîtier dispose en outre d'une zone de lecture, d'un bouton

de réglage de la température et d'un bouton d'étalonnage.

-  Un troisième bouton permet en général de sélectionner le calibre.

 

Titrage conductimétrique : Exemple de montage

 

-  Le suivi du titrage par conductimétrie permet de tracer le graphe σ = f (VB).
-  Exemple de graphe obtenue :

 

Exemple : Suivi par conductimétrie

-  Le réactif titré A est mis dans un bécher ou un erlenmeyer.
-  Le réactif titrant B est mis dans la burette de Mohr (burette graduée).

Titrer une espèce chimique en solution,

c’est déterminer sa concentration molaire dans la solution

Le but du titrage ou d’un dosage est de déterminer

la concentration molaire d’une espèce chimique M présente

dans un volume donné et précis d’une solution.

L’outil de détermination de cette quantité de matière est la réaction chimique :

C’est la réaction de dosage ou de titrage.

Cette réaction doit être rapide, totale, spécifique et unique.
-   Le réactif titré A est mis dans un bécher ou un erlenmeyer.
-  Le réactif titrant B est mis dans la burette de Mohr (burette graduée)

 

 Équivalence d’un titrage :

 

Équivalence d’un titrage :

À l’équivalence, les réactifs sont dans les proportions stœchiométriques définies

par les coefficients de la réaction. À l’équivalence, il n’y a pas de réactif limitant.

 

Avant l’équivalence

Le réactif titrant est totalement consommé, c’est le réactif limitant

Il reste encore du réactif titré : il est en excès.

 

À l’équivalence :

Le réactif titrant et le réactif titré sont totalement consommés.

Ils sont tous les deux limitants (mélange stœchiométrique).
 

Après l’équivalence

Le réactif titré est totalement consommé : c’est le réactif limitant.

Maintenant, c’est le réactif titrant qui est en excès.

 

En conclusion

À l’équivalence du titrage, il y a changement de réactif limitant

 

 

La détermination de la concentration du réactif titré :

-  Au cours du titrage, le réactif titrant est versé jusqu’à ce que le réactif titré ait totalement réagi :
-  Alors on dit que l’équivalence est atteinte.
-  L’équivalence :
-  il y a équivalence lorsque les réactifs ont été mélangés dans les proportions stœchiométriques de la réaction.
-  C’est-à-dire lorsqu’on a réalisé un mélange stœchiométrique des réactifs titré et titrant.
-  Les deux réactifs de la réaction sont alors totalement consommés.
-  Avant l’équivalence :
-  Le réactif titrant est totalement consommé, c’est le réactif limitant
-  Il reste encore du réactif titré : il est en excès.
-  À l’équivalence :
-  Le réactif titrant et le réactif titré sont totalement consommés.
-  Ils sont tous les deux limitants (mélange stœchiométrique).
-  Après l’équivalence :
-  Le réactif titré est totalement consommé : c’est le réactif limitant.
-  Maintenant, c’est le réactif titrant qui est en excès.
-  En conclusion :
-  À l’équivalence du titrage, il y a changement de réactif limitant.

Repérage de l’équivalence :

-  Lors d’un titrage colorimétrique, on repère l’équivalence par un changement de couleur du mélange réactionnel.
-  C’est le cas lorsque l’on teste une espèce colorée.
-  Il est parfois possible d’utiliser un indicateur de fin de réaction pour observer un changement de couleur à l’équivalence si les réactifs ne sont pas colorés.
-  On ajoute alors un indicateur coloré adapté à la réaction chimique.
-  Exemple : Dosage du diiode I2 (aq) par les ions thiosulfate S2O32- (aq).
-  L’équivalence est repérée par un changement de couleur :
-  Le diiode I2 (aq), seule espèce colorée du système chimique étudié, n’est plus présent à l’équivalence.
-  La solution devient incolore.
-  Toutefois, l’équivalence étant difficile à repérer, on ajoute juste avant l’équivalence un indicateur coloré, l’empois d’amidon, qui permet de repérer plus facilement l’équivalence.

Relation à l’équivalence :

-  L’équation support de dosage s’écrit :

3 A + B → C + 2 D

-  À l’équivalence du titrage, on a réalisé un mélange stœchiométrique des réactifs titrant et titré.
-  La relation à l’équivalence du titrage s’écrit :
-   
-  Comme on travaille avec des volumes et des concentrations, on peut affiner cette relation :
-  Quantité de matière initiale du réactif titré A :
-  On connaît le volume utilisé : VA
-  La concentration du réactif titré A : CA = ?
-  n0 (A) = CA . VA
-  Quantité de matière à l’équivalence du réactif titrant B :
-  Volume versé à l’équivalence du réactif titrant B : VB = VE
-  Le volume VE est le volume versé de solution titrante lorsque l’équivalence est atteinte.
-  La concentration du réactif titrant est connue : CB
-  n0 (B) = CB . VE
-  En conclusion :

 

-  On en déduit la concentration CA du réactif titré recherché :
-   

3 A + B → C + 2 D

-  Pour retrouver la relation :

Équation

3 A

+

B

→

Quantité de matière

n (A)

 

n (B)

 

Coefficients stœchiométriques

3

 

1

 
-  Relation :

 

haut