|
|
Les lentilles minces convergentes Exercices |
|
|
|
|
1)- Exercice 04 page 314 : Estimer une distance focale :
|
Estimer une distance focale : 1.
Proposer un protocole expérimental afin
d’estimer la distance focale f’ d’une lentille mince convergente. 2.
Schématiser l’expérience en indiquant la
grandeur mesurée. |
|
Estimer une distance focale : 1.
Protocole expérimental afin d’estimer la
distance focale f’ d’une lentille mince convergente.
-
La relation de conjugaison
est la suivante pour une lentille mince convergente.
-
-
Si on vise un objet
AB
suffisamment éloigné de la lentille,
-
Le terme
xA devient très grand et le terme
-
En conséquence,
-
-
La distance entre la
lentille et l’image est pratiquement égale à la distance focale de
la lentille.
-
On forme donc l’image d’un objet
suffisamment éloigné (exemple : le Soleil) sur un écran.
-
La distance entre le centre de la
lentille et l’image de l’objet correspond pratiquement à la distance
focale de la lentille. 2.
Schéma l’expérience :
-
Une lentille, dont l’axe
optique est dirigé vers le Soleil, donne sur un écran une tache quasi ponctuelle très lumineuse.
-
Cette tache représente
l’image du Soleil (Attention
ça chauffe).
-
On peut considérer que le
Soleil est une source lumineuse située à l’infini.
-
Les rayons lumineux provenant du
Soleil sont considérés comme parallèles.
-
Tout rayon incident parallèle à l’axe
principal d’une lentille convergente en émerge en passant par le
point F’ appelé foyer - image de la lentille.
-
La distance f’: distance
focale de la lentille mince convergente.
-
OF =
f’ |
2)- Exercice 06 page 314 : Utiliser la relation de conjugaison (1) :
|
Utiliser la relation de conjugaison (1) Un objet AB est situé à 20,0 cm d’une lentille mince
convergente. Son image se forme sur un écran situé à 33,3 cm de la lentille.
-
Utiliser la relation de conjugaison
pour calculer la distance focale
f’ de la lentille mince convergente.
-
Donnée :
-
Relation de conjugaison :
|
|
Utiliser la relation de conjugaison (1)
-
Valeur de la distance focale f’ de la lentille mince convergente.
-
Dans un premier temps, peut faire un
schéma sans soucis d’échelle.
-
Schéma :
-
Le rayon lumineux qui passe par le
centre optique O de la
lentille mince convergente n’est pas dévié.
-
Les différentes valeurs :
-
La grandeur
xA = – 20,0 cm
et xA’ = 33,3
cm
-
Relation de conjugaison :
-
-
On peut déterminer la valeur du
grandissement de l’image :
-
-
On peut en déduire les
caractéristiques de l’image :
-
L’image est réelle.
-
γ <
0
l’image est de sens contraire à l’objet, l’image est
renversée.
-
| γ | >1, l’image est plus
grande que l’objet. |
3)- Exercice 07 page 314 : Utiliser la relation de conjugaison (2) :
|
Utiliser la relation de conjugaison (2) :
-
Utiliser
la relation de conjugaison pour calculer l’abscisse
xA’ de l’image A’B’
pour la situation décrite ci-dessus.
-
Donnée :
-
Relation de conjugaison :
|
Utiliser la relation de conjugaison (2) :
-
Schéma avec le repère
R (0,
x,
y) :
-
Exploitation du graphique :
-
Les différentes mesures :
-
Abscisse du point objet
A : xA ≈ – 6,0
cm
-
Mesure de la distance focale
f’ :
f’ ≈ 10 cm
-
Pour déterminer la valeur de
l’abscisse xA’
du point image A’, on
utilise la relation de conjugaison :
-
-
On peut déterminer la valeur du
grandissement de l’image :
-
-
On peut en déduire les
caractéristiques de l’image :
-
L’image est virtuelle.
-
γ >
0
l’image est de même sens que l’objet, l’image est
droite.
-
| γ | >1, l’image est plus
grande que l’objet.
-
Construction de l’image
A’B’ de l’objet
AB.
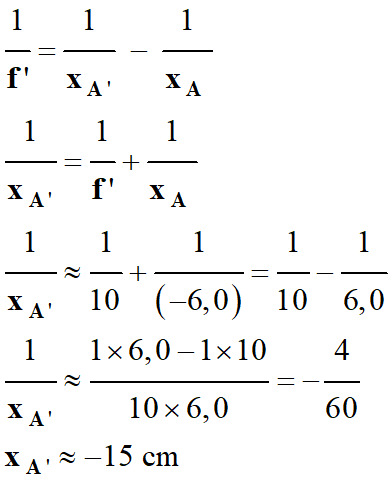
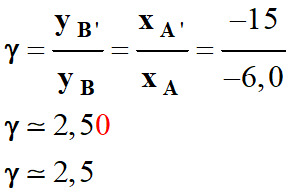
![]()
4)- Exercice 08 page 315 : Calculer le grandissement :
|
Calculer le grandissement : Un objet AB de 2,0 cm de hauteur donne, à travers une
lentille convergente,une image renversée de 1,0 cm de hauteur.
-
Calculer le grandissement
γ dans ces conditions.
-
Donnée :
-
Relation de grandissement :
|
Calculer le grandissement :
-
Grandissement
γ dans ces conditions :
-
Relation de grandissement :
-
-
On peut réaliser un schéma même
si on ne connait les abscisses des points A et A' :
-
On représente le rayon lumineux qui
passe par le centre optique de la lentille et qui n’est pas dévié.
-
Avec le repère associé à la lentille
convergente mince, on peut déterminer les ordonnées des points
B et B’.
-
On ne connaît pas les abscisses des
points A et
A’, ni la distance focale f’ -
On peut déterminer la valeur du
grandissement de l’image :
-
-
Caractéristiques de l’image :
-
L’image est réelle.
-
γ <
0
l’image est de sens contraire à l’objet, l’image est
renversée.
-
| γ | < 1, l’image est plus
petite que l’objet.


![]()
5)- Exercice 09 page 315 : Utiliser la formule du grandissement :
|
Utiliser la formule du grandissement : Schéma : 1.
En utilisant le schéma ci-dessus, calculer
le grandissement γ dans ces conditions. 2.
En déduire l’abscisse xA’
de l’image A’B’.
-
Donnée :
-
Relation de grandissement :
|
|
Utiliser la formule du grandissement :
-
Schéma : 1.
Grandissement γ dans ces conditions.
-
Coordonnées des différents points
dans le repère associé à la lentille :
-
Abscisses du point
A : xA = – 5,0
cm
-
Abscisses du point
A’ : xA’ = ?
-
Ordonnées du point
B : yB = 3,0
cm
-
Ordonnées du point
B’ : yB’ = –
4,5 cm
-
Relation de grandissement :
-
-
Caractéristiques de l’image :
-
L’image est réelle.
-
γ <
0
l’image est de sens contraire à l’objet, l’image est
renversée.
-
| γ | > 1, l’image est plus
grande que l’objet. 2.
Valeur de l’abscisse xA’
de l’image A’B’.
-
À partir de la relation de
grandissement, on peut retrouver la valeur de l’abscisse xA’
de l’image A’B’.
-
-
On peut en déduire la valeur de la
distance focale f’ de la
lentille :
-
-
Schéma complet : |
6)- Exercice 10 page 315 : Distinguer image virtuelle d’image réelle :
|
Distinguer image virtuelle d’image réelle : Comment différencier une image réelle d’une image virtuelle ? |
|
Différencier une image réelle d’une image virtuelle :
-
Objet réel et image virtuelle :
-
Un point image est virtuel s’il est
le sommet d’un faisceau lumineux qui émerge de l’appareil en
divergeant.
-
L’œil placé derrière l’instrument
voit les images virtuelles.
-
Objet virtuel et image réelle :
-
Un point objet est virtuel s’il est
le sommet d’un faisceau lumineux qui entre dans l’appareil en
convergeant.
-
Remarque : si les rayons passent
effectivement par le point considéré celui-ci est réel.
-
Si ce sont les prolongements des
rayons qui passent par ce point, alors il est virtuel.
-
L’image virtuelle :
-
Exemple d’image virtuelle :
-
L’image formée à travers la
lentille ne peut pas être observée sur un écran.
-
Ce sont les prolongements
des rayons 1, 2 et 3 qui se coupent en
B’
-
Elle ne se forme pas sur un
écran mais elle peut être vue par l’œil à travers le système
optique.
-
Il faut placer l’œil sur le
chemin des rayons lumineux qui émergent du système optique.
-
Image
réelle :
-
Exemple d’image réelle :
-
L’image formée à travers la
lentille peut être observée sur un écran.
-
Les
rayons 1, 2 et 3 qui se
coupent effectivement en
B’ (et non les
prolongements) |
7)- Exercice 16 page 316 : Prévoir les caractéristiques d’une image :
|
Prévoir les caractéristiques d’une image : Un objet AB est situé à 5,0 cm d’une lentille mince
convergente. L’image A’B’ de cet objet a pour abscisse xA’
= – 10 cm. 1.
Calculer le grandissement γ dans ces
conditions. 2.
Donner les caractéristiques de l’image :
-
Virtuelle ou réelle ;
-
Plus petite ou plus grande que
l’objet :
-
Renversée ou droite par rapport à
l’objet.
-
Donnée :
-
Relation de grandissement :
|
|
Prévoir les caractéristiques d’une image : 1.
Valeur du grandissement
γ dans ces conditions.
-
Les données :
-
L’objet
AB est situé à 5,0 cm
d’une lentille mince convergente.
-
L’image
A’B’
de cet objet a pour abscisse
xA’ = – 10 cm.
-
On peut faire un schéma de la
situation sans soucis d’échelle :
-
Abscisse du point objet
xA :
-
xA = – 5,0 cm
-
Valeur du grandissement :
-
2.
Les caractéristiques de l’image :
-
L’image est virtuelle. -
-
γ >
0 l’image est de même
sens que l’objet, elle est droite.
-
| γ | >1, l’image est plus
grande que l’objet.
Additif :
-
On peut déterminer la valeur de la
distance focale f’ de la
lentille :
|
8)- Exercice 24 page 318 : Un mini-projecteur :
|
Un mini-projecteur : Un dispositif de projection pour smartphone est constitué d’une lentille mince convergente de distance focale f’ = 15,0 cm. L’écran du smartphone, constituant l’objet à projeter, a une hauteur de 7,0 cm. Il est placé à 18,0 cm de la lentille du
dispositif de projection. 1.
À partir de la position de l’objet, calculer
l’abscisse de l’image formée par la lentille. 2.
Réaliser un schéma à l’échelle 1 cm sur la
feuille pour 10 cm dans la réalité. 3.
Caractéristiques de l’image : a.
Déterminer graphiquement la position et la
taille de l’image. b.
Calculer le grandissement à partir des
résultats obtenus sur le graphique. 4.
Que signifie le signe de ce grandissement ?
-
Données :
-
Relation de conjugaison :
-
Relation de grandissement :
|
Un mini-projecteur : 1.
Valeur de l’abscisse de l’image formée par
la lentille.
-
Schéma préparatoire avec le repère
associé à la lentille :
-
Distance focale
f’ = 15,0 cm.
-
Hauteur de l’objet :
7,0 cm
-
Distance de l’objet à la lentille :
18,0 cm
-
À l’aide du schéma, on peut donner
les coordonnées des points objets
A et
B :
-
Abscisse du point objet A :
-
xA = – 18,0 cm
-
Ordonnée du point objet B :
-
yB = 7,0 cm 2.
Schéma. Échelle : 1 cm (feuille) ↔ 10 cm (réalité)
-
La construction est assez délicate à
faire, surtout avec l’échelle choisie.
-
On peut déterminer la valeur de
l’abscisse du point image A’
à l’aide de la relation de conjugaison.
-
-
Avec le grandissement, on peut
connaître la taille de l’image
A’B’
:
-
-
On en déduit la valeur de l’ordonné e
yB’ du point
image B’ :
-
3.
Caractéristiques de l’image : a.
Détermination graphique de la position et de
la taille de l’image.
-
Maintenant, on peut réaliser la
construction.
-
On trace les 3 rayons
caractéristiques :
-
Rayon
1 : issu du point
B
et
passant par le centre optique : il n’est pas dévié.
-
Rayon
2 : issu du point
B,
ce rayon est parallèle à l’axe optique. - Il émerge de la lentille
en passant par le point
F’ foyer - image.
-
Rayon 3 :
issu du point
B
et passant par
F (foyer - objet). - Il émerge de la lentille parallèlement à
l’axe optique. b.
Valeur du grandissement à partir du
graphique.
-
Par lecture graphique, on peut donner
les ordonnées du point objet
B et du point image B’.
-
yB = 7,0 cm
-
yB’ ≈ – 35, cm
-
Valeur du grandissement :
-
4.
Le signe de ce grandissement :
-
Caractéristiques de l’image :
-
γ = – 5,0
-
L’image est réelle.
-
γ <
0 l’image est de
sens contraire à l’objet, elle est renversée.
-
| γ | > 1, l’image est plus
grande que l’objet.
-
L’image est 5 fois plus grande que
l’objet.
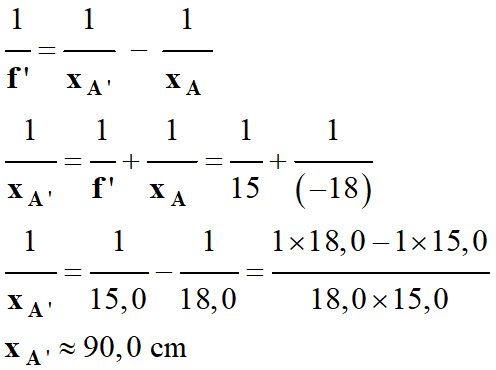
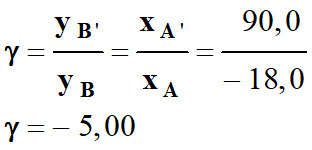
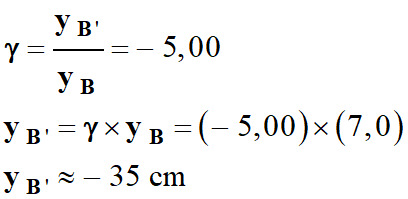
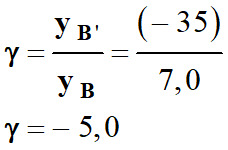
![]()
9)- Exercice 25 page 318 : Focométrie :
|
Focométrie : Pour déterminer la distance focale d’une lentille mince convergente, on mesure pour différentes abscisses xA d’un
objet AB placé sur le banc d’optique, les abscisses xA’ de son
image A’B’. Les résultats sont inscrits dans le tableau ci-dessous :
1.
Représenter
2.
Déterminer l’équation de la courbe obtenue. 3.
Déduire de l’équation de la courbe la
distance focale f’ de la lentille mince convergente. 4.
Le protocole étant répété cinq fois dans les
mêmes conditions, on obtient les résultats suivants :
-
Déterminer la distance
f’ et l’incertitude-type u
(f’) (fiche page 361)
-
Donnée :
-
Relation de conjugaison : |
Focométrie :
-
Tableau de valeurs : xA
(m)
–0,400
–0,300
–0,200
–0,150
xA’
(m)
0,135
0,145
0,202
0,298 1.
Représentation de
-
Grandeur en abscisse :
-
Grandeur en ordonnée :
-
Représentation graphique : 2.
Équation de la courbe obtenue :
-
Les points sont sensiblement alignés.
On peut tracer la droite moyenne.
-
Celle-ci ne passe pas par l’origine.
-
Le phénomène est modélisé par une
fonction affine dont l'équation est du type :
-
y
=
a .
x + b.
-
Avec les grandeurs choisies, on peut
écrire :
-
-
Il faut déterminer les valeurs de
a et
b.
-
"a"
est le coefficient directeur de la droite moyenne tracée.
-
"b"
représente l’ordonnée à l’origine.
-
Les grandeurs
x et y ne sont pas
proportionnelles !
-
Détermination de la valeur de
a :
-
Pour déterminer la valeur de "a",
on repère 2 points, de la droite moyenne tracée, éloignés l'un de l'autre (A
et B).
-
-
Dans le cas présent, la grandeur
a n’a pas d’unité.
-
Ordonnée à l’origine : par lecture
graphique :
-
b ≈ 10 m–1.
-
Équation de la droite moyenne :
-
-
Relation que l’on peut écrire de la
façon suivante :
-
-
Retour sur l’équation de la droite
sous la forme suivante :
-
-
La grandeur
b ≈ 10 m–1.
-
En physique, cette grandeur
représente la vergence C
de la lentille :
-
b =
C = 10 δ (dioptrie)
-
-
La relation de conjugaison peut
s’écrire sous la forme suivante :
-
Additif :
-
On peut réaliser une étude
statistique de la série de valeurs avec le tableur Excel.
-
Dans le cas présent, on est en
présence d’une série de 4 mesures (ce qui est un peu juste).
-
Pour effectuer une étude statistique,
il faut au moins une douzaine de valeurs.
-
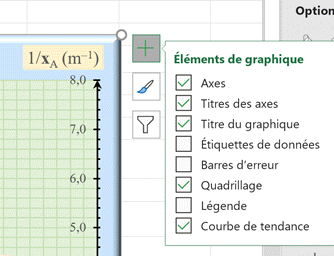
On
sélectionne le graphique :
-
On clique sur le
+ et on coche ‘Courbe de tendance’.
-
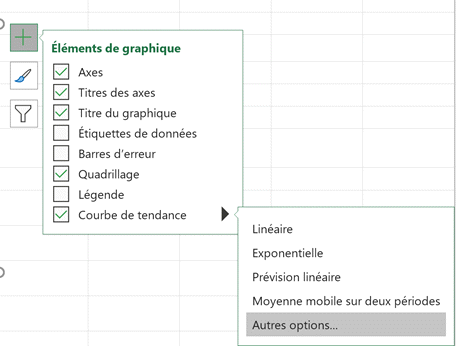
On place la souris sur ‘Courbe de
tendance’,
- puis on sélectionne ‘Autres options’.
-
On coche : ‘Linéaire’ ,
-
‘Afficher l’équation sur le
graphique’
- et ‘Afficher le coefficient de détermination (R²) sur le
graphique’.
-
On obtient le graphe suivant :
-
Équation de la droite tracée :
-
y ≈ 1,0
x + 10
-
Traduction :
-
3.
Valeur de la distance focale f’ de la
lentille mince convergente.
-
La relation de conjugaison :
-
-
En identifiant les différents
termes :
-
4.
Déterminer la distance f’ et
l’incertitude-type u (f’) : f’
(cm)
10,2
10,0
10,1
9,9
9,8
-
L’incertitude-type
u (f’) est estimée par la
relation suivante :
-
-
N représente le nombre de
fois ou le protocole a été répété :
-
N = 5
-
La grandeur
σn–1
représente l’écart-type :
-
-
L’effectif, noté
ni, est le nombre de mesures donnant le résultat
xi.
-
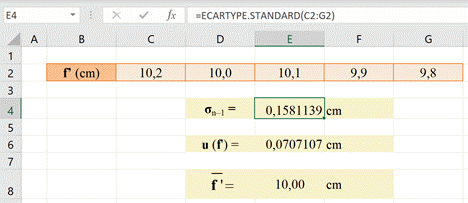
On peut calculer l’écart-type avec
une calculatrice ou un tableur :
-
Avec le tableur Excel :
-
Valeur que l’on exprime avec deux
chiffres significatifs :
-
σn–1,≈ 0,16 cm
-
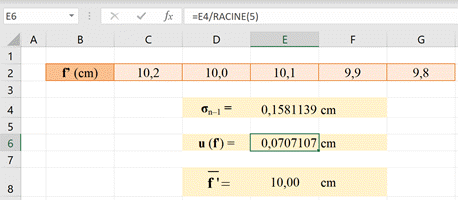
L’incertitude-type
u (f’) :
-
-
L’incertitude-type
u (f’) est arrondie
généralement par excès en ne conservant qu’un seul chiffre
significatif :
-
u
(f’) ≈ 0,08 cm
-
Valeur moyenne
-
-
Conclusion :
-
-
f’ = (10 ± 0,08) cm
-
9,92 cm ≤
f’ ≤ 10,08 cm
-
9,92 cm ≤
f’ ≤ 10,1 cm
![]() en fonction de :
en fonction de :![]()
![]()
![]()

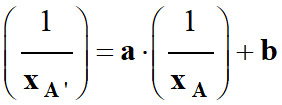
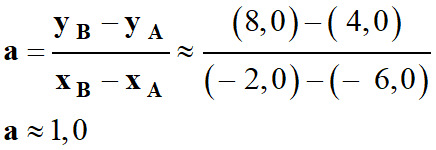
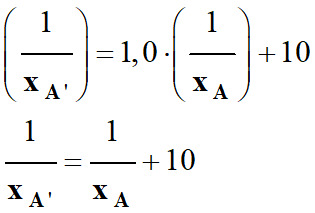

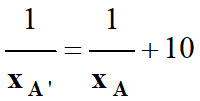
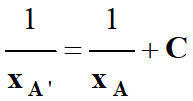
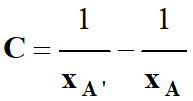
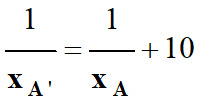
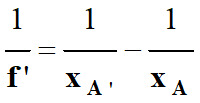
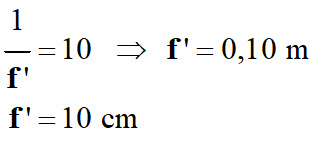
![]()
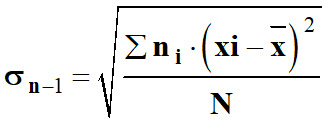
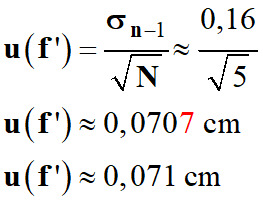
![]() de la distance focale :
de la distance focale :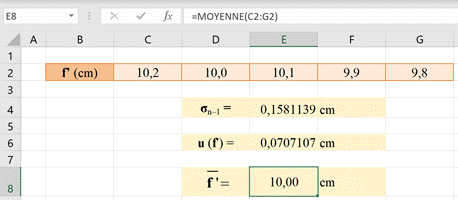
![]()
![]()
![]()
10)- Exercice 27 page 318 : Côté maths : Grandissement et théorème de Thalès :
|
Côté maths : Grandissement et théorème de Thalès : Schéma :
-
Utiliser le théorème de Thalès pour
démontrer la relation de grandissement :
-
|
|
Côté maths : Grandissement et théorème de Thalès :
-
Relation de grandissement :
-
-
Considérons les triangles
OAB et OA’B’ :
-
Les droites (AB) et (A’B’)
sont parallèles.
-
Et les droites (AA’) et (BB’) se coupent
au point O :
-
L’application du théorème de Thalès
permet d’écrire la relation suivante :
-
-
Grâce au repère associé à la
lentille, on peut relier les mesures algébriques aux coordonnées des
différents points :
-
Schéma :
-
-
On en déduit la relation suivante :
-
-
C’est bien la relation de
grandissement. |
|
|