|
|
Les réactions de combustion Exercices |
|
|
|
|
|
Exercices :
1)- Exercice 03
page 164 : Écrire l’équation d’une réaction de combustion.
2)- Exercice 05
page 164 : Calculer une énergie libérée.
3)- Exercice 07
page 164 : Déterminer une énergie de liaison.
4)- Exercice 08
page 164 : Estimer une énergie de combustion.
5)- Exercice 09
page 165 : Choisir un combustible.
6)- Exercice 11
page 165 : Élimination du CO2
d’un véhicule GPL.
7)- Exercice 12
page 165 :Composition du carburant E15.
8)- Exercice 15
page 166 : Valeur énergétique d’une amande. 9)- DS N° 01 : Exercice 16 page 167 :
Quel carburant pour les véhicules « Flex-fuel » ?
(40 min) 10)- DS N° 02 : Exercice 17 page 167 :
À propos du « gaz à l’eau » (15 min) |
1)- Exercice 03 page 164 : Écrire l’équation d’une réaction de combustion :
|
Écrire l’équation d’une réaction de combustion :
-
Recopier et ajuster les équations des
réactions de combustions suivantes :
a)- CH4 (g) + … O2
(g) → … CO2
(g) + … H2O (g) b)-
C2H6
(g) + … O2 (g)
→ … CO2 (g) + … H2O
(g) c)-
C3H8O
(g) + … O2 (g)
→ … CO2 (g) + … H2O
(g) |
|
Écrire l’équation d’une réaction de combustion :
-
Équations des réactions de
combustions complètes :
-
Méthode :
-
On équilibre :
-
En premier l’élément carbone C
;
-
Puis l’élément hydrogène
H
-
Et enfin l’élément oxygène
O. - Si pour l’élément oxygène, on obtient un nombre impair, on peut multiplier par deux les différents coefficients
stœchiométriques.
a)- 1
CH4 (g)
+ 2 O2
(g) →
1 CO2 (g) +
2 H2O
(g) b)-
2 C2H6
(g) + 7 O2 (g)
→ 4 CO2
(g) + 6 H2O
(g) c)-
2 C3H8O
(g) + 9 O2
(g) →
6 CO2 (g) +
8 H2O
(g) |
2)- Exercice 05 page 164 : Calculer une énergie libérée :
|
Calculer une énergie libérée : Pour réchauffer des aliments, il est possible d’utiliser une
bouteille de gaz de butane C4H10. Une bouteille contient une masse m = 227 g de butane.
-
Déterminer l’énergie libérée lors de
la combustion de la totalité du butane contenu dans la bouteille.
-
On donne
PC (butane) = 46,4 MJ .
kg–1 |
|
Calculer une énergie libérée :
-
Énergie
libérée lors de la combustion
de la totalité du butane contenu dans la bouteille.
-
On donne
PC (butane) = 46,4 MJ .
kg–1
-
PC représente le pouvoir
calorifique du butane :
-
Formule du butane
C4H10.
-
Masse de butane :
m = 227 g
-
Relation :
-
Q =
– m . PC
-
Q
= – 227×
10–3 ×
46,4
-
Q ≈ – 10,53
MJ
-
Q ≈ – 10,5 MJ - Q < 0 - Cette énergie est définie par rapport
au système chimique qui contient le combustible.
-
Le système chimique est le système de
référence.
-
Il cède de l’énergie au milieu
extérieur. |
3)- Exercice 07 page 164 : Déterminer une énergie de liaison :
|
Déterminer une énergie de liaison : Le dihydrogène H2 (g) est un combustible des
piles à hydrogène. Il brûle au contact du dioxygène O2 (g) selon
la réaction suivante : H2 (g) + ½
O2 (g) →
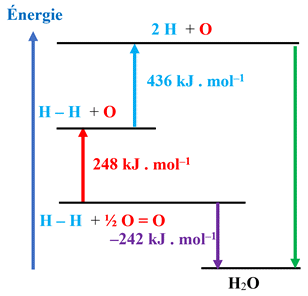
H2O (g) Diagramme énergétique :
1.
Citer un autre combustible utilisé dans les
transports. 2.
À l’aide du diagramme, estimer la valeur de
l’énergie de liaison O – H dans l’eau. |
Déterminer une énergie de liaison : 1.
Autre combustible utilisé dans les
transports :
-
Le diesel ou gazole
-
Essence, 2.
Valeur de l’énergie de liaison O –
H dans l’eau.
-
Eℓ (O – H)
-
L’énergie de liaison Eℓ
d’une liaison covalente A
– B,
est l’énergie nécessaire pour rompre une mole de
liaisons
et libérer les atomes isolés A et B à l’état
gazeux.
-
L’équation de la réaction : H – H
(g) + ½
O
= O (g) →
H – O
– H (g)
-
Au cours de la combustion d’une mole
de dihydrogène :
-
Les liaisons rompues :
-
1
× 1 mole liaisons H – H
- ½
× 1 mole de liaisons O = O
-
Eℓrompues =
1 × Eℓ (H – H) +
½
× Eℓ (O = O)
-
Les liaisons formées :
-
1
× 2 moles de liaisons H – O
sont formées.
-
Eℓformées =
1 × 2 × Eℓ (H
– O)
-
Énergie molaire de combustion du
dihydrogène :
-
Ecomb (H2)
= Eℓrompues – Eℓformées
-
Par lecture graphique :
-
1 × Eℓ (H – H) = 436 kJ . mol–1
-
½
× Eℓ (O = O) = 248 kJ . mol–1
-
2
× Eℓ (H
– O) = (– 436 – 248 – 242)
-
Eℓ (H – O) =
( 436 + 248 + 242) /
2
-
Eℓ (H – O) =
463 kJ . mol–1 - Énergie molaire de combustion du
dihydrogène :
-
Ecomb (H2)
= Eℓrompues – Eℓformées
-
Ecomb (H2)
= 436 + 248 – 2 × 463
-
Ecomb (H2)
= – 242 kJ . mol–1
![]()
4)- Exercice 08 page 164 : Estimer une énergie de combustion :
|
Estimer une énergie de combustion : À la campagne certains habitants utilisent du gaz propane pour se
chauffer. 1.
Citer un autre combustible usuel utilisé
dans l’habitat. 2.
Écrire l’équation de la réaction de
combustion du propane. 3.
Dénombrer les liaisons rompues et formées. 4.
En déduire l’énergie molaire de combustion
du propane.
-
Données :
|
Estimer une énergie de combustion : 1.
Autre combustible usuel utilisé dans
l’habitat.
-
Le fuel ;
-
L’éthanol (alcool) comme chauffage
d’appoint 2.
Équation de la réaction de combustion du
propane.
1
C3H8
(g) +
5
O2 (g)
→
3
CO2 (g) +
4
H2O (g) 3.
Dénombrer les liaisons rompues et formées.
-
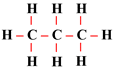
Structure des différentes molécules :
Propane
Dioxygène
Dioxyde de carbone
Eau
O
= O
O
= C
=
O
H — O — H ►
Les liaisons
rompues :
-
1
× 8 moles de liaisons C – H
-
1
× 2 moles de liaisons C – C
-
5
× 1 moles de liaisons O = O
-
3
× 2 moles de liaisons C = O
-
4
× 2 moles de liaisons H – O 4.
Énergie molaire de combustion du propane.
-
Somme des énergies des liaisons
rompues
-
Eℓrompues =
8 × Eℓ (C – H) +
2 × Eℓ (C –
C) +
5 × Eℓ (O =
O)
-
Eℓrompues =
8 × 413 +
2
× 348 +
5
× 496
-
Eℓrompues ≈ 6,48 ×
103 kJ . mol–1
-
Somme des énergies des liaisons
formées :
-
Eℓformées =
6 × Eℓ (C =
O) + 4 × 2 × Eℓ
(H – O)
-
Eℓformées =
6 × 796 +
8 × 463
-
Eℓformées
= 8,48 × 103 kJ . mol–1
-
Énergie molaire de combustion du
propane :
-
Ecomb (C3H8)
= Eℓrompues – Eℓformées
-
Ecomb (C3H8)
≈ 6,48 × 103 – 8,48 × 103
-
Ecomb (C3H8)
≈ – 2,00 × 103
kJ . mol–1 -
Les réactions de combustion sont exothermiques : - Elles libèrent plus d’énergie qu’elles n’en consomment. -
Ecomb < 0.
![]()
5)- Exercice 09 page 165 : Choisir un combustible :
|
Choisir un combustible :
-
Écrire les équations de combustion
complète du méthane CH4 (g) et du butane C4H10
(g).
-
Évaluer la masse de dioxyde de
carbone CO2 (g) produite par chacune des réactions
de combustion lorsqu’elles libèrent une énergie Q = – 200
kJ.
-
En déduire pour une même énergie
libérée, le combustible qui génère le moins de CO2.
-
Données :
-
M (CO2) =
44,0 g . mol–1
-
Ecomb (CH4)
= – 800 kJ . mol–1.
-
Ecomb (C4H10)
= – 2900 kJ . mol–1. |
|
Choisir un combustible :
-
Équations de combustion complète du
méthane CH4 (g) et du butane C4H10
(g).
-
Combustion complète du méthane :
-
Combustion complète du butane :
-
Masse de dioxyde de carbone CO2
(g) produite par chacune des réactions de combustion :
-
Énergie
libérée : Q = – 200
kJ.
►
Énergie transférée Q par la
combustion d’une quantité n de combustible :
-
Q =
n .
Ecomb
-
Tableau :
-
Pour le méthane :
-
Q = n
(CH4)
. Ecomb (CH4)
-
Pour le butane :
-
Q = n
(C4H10)
. Ecomb (C4H10)
-
L’énergie transférée Q peut
aussi se calculer à partir du pouvoir calorifique
PC :
-
Comme on veut connaître la masse de
dioxyde de carbone produite, :
►
Cas du méthane :
-
La combustion de
1 mole de méthane génère la formation de
1 mole de dioxyde de carbone :
-
n (CH4)
= n (CO2)
-
comme on veut connaître la masse de
dioxyde de carbone, on utilise la relation suivante :
-
m (CO2)
= n (CO2) .
M (CO2)
-
En combinant les relations, on
obtient :
-
Q = n (CH4)
. Ecomb (CH4)
= n (CO2)
. Ecomb (CH4)
-
-
et
m (CO2)
= n (CO2)
. M (CO2)
-
-
Application numérique :
-
►
Cas du butane :
-
La combustion de
1 mole de butane génère la formation de
4 moles de dioxyde de carbone :
-
n (CO2)
= 4 n (C4H10)
-
-
Application numérique :
-
-
Combustible qui génère le moins de
CO2.
-
Le méthane CH4 (g) génère moins de dioxyde de
carbone CO2 (g) que le butane C4H10
(g). |
6)- Exercice 11 page 165 : Élimination du CO2 d’un véhicule GPL :
|
Élimination du CO2
d’un véhicule GPL : Un véhicule fonctionnant au GPL (gaz de pétrole liquéfié) consomme en moyenne 10,0 L de carburant au 100 km. Le GPL utilisé est constitué en volume d’un mélange de 50
% de butane C4H10 et 50 % de propane C3H8.
-
Comparer la masse de dioxyde de
carbone produite par ce véhicule sur un parcours de 1,0 km à celle d’un véhicule à essence de classe
A. 1.
Écrire les formules semi-développées du
propane et du butane. 2.
Écrire les équations de réaction de
combustion complète. 3.
Calculer, pour 1,0 km parcouru, la masse de
dioxyde de carbone rejeté dans l’atmosphère par la combustion :
-
Du butane consommé ;
-
Du propane consommé. 4.
Comparer la masse de dioxyde de carbone
produite par ce véhicule sur un parcours de 1,0 km à celle d’un
véhicule à essence de classe A.
-
Données :
-
ρbutane,liq
= 585 g . L–1
-
ρpropane,liq =
515 g . L–1
-
M (C4H10)
= 58,0 g . mol–1
-
M (C3H8)
= 44,0 g . mol–1
-
M (CO2)
= 44,0 g . mol–1
-
Un véhicule de classe
A rejette au maximum 100 g de
CO2 par kilomètre parcouru. |
|
Élimination du CO2
d’un véhicule GPL : Un véhicule fonctionnant au GPL (gaz de pétrole
liquéfié) :
-
Consommation :
-
C
= 0,100 L . km–1
-
Le
GPL est
constitué d’un mélange en volume :
-
de 50 % de butane C4H10
et 50 % de propane C3H8.
-
Données :
-
ρbutane,liq
= 585 g . L–1
-
ρpropane,liq
= 515 g . L–1
-
M
(C4H10) = 58,0 g . mol–1
-
M
(C3H8) = 44,0 g . mol–1
-
M
(CO2) = 44,0 g . mol–1
-
Un véhicule de classe
A
rejette au maximum 100 g de
CO2 par kilomètre parcouru. 1.
Formules semi-développées du propane et du
butane.
-
Le propane :
-
Le butane : 2.
Écrire les équations de réaction de
combustion complète.
-
Combustion complète du
propane :
-
Combustion complète du
butane :
3. Calcul, pour 1,0 km parcouru, de la masse de dioxyde de carbone rejeté dans l’atmosphère par la combustion :
►
Du butane consommé ;
-
Volume de butane liquide
consommé pour 1 km :
-
-
Masse de butane consommé
pour 1 km
-
-
Quantité de matière de
butane consommé pour 1 km :
-
-
Quantité de matière de
dioxyde de carbone produit :
-
La combustion de
1
mole de butane
produit
4 moles de dioxyde de carbone :
-
n
(CO2) =
4 n (C4H10)
-
-
Et enfin , masse de
CO2 formé :
-
-
Application numérique :
-
►
Du propane consommé :
-
Volume de propane liquide
consommé pour 1 km :
-
-
Masse de propane consommé
pour 1 km
-
-
Quantité de matière de
propane consommé pour 1 km :
-
-
Quantité de matière de
dioxyde de carbone produit :
-
La combustion de
1
mole de propane
produit
3 moles de dioxyde de carbone :
-
n
(CO2) =
3 n (C3H8)
-
-
Et enfin , masse de
CO2 formé :
-
-
Application numérique :
-
-
Masse de dioxyde de carbone
produite par ce véhicule sur un parcours de 1,0 km :
-
m
(CO2) ≈ 88,8 + 61,8
-
m
(CO2) ≈ 88,8 + 77,3
-
m
(CO2) ≈ 166 g
-
Un véhicule de classe
A
rejette au maximum 100 g de
CO2 par kilomètre parcouru. - Le véhicule fonctionnant au GPL rejette, au km, plus de dioxyde de carbone que le véhicule de classe
A. |
7)- Exercice 12 page 165 : Composition du carburant E 15 :
|
Composition du carburant E 15 : Le carburant E 15, mélange d’essence et d’agroéthanol,
limite la consommation d’énergie fossile. 1.
Écrire l’équation de la réaction de
combustion complète de l’éthanol C2H6O
(ℓ). 2.
Estimer l’énergie molaire de combustion de
l’éthanol et en déduire le pouvoir calorifique de l’éthanol. 3. Sachant que le pouvoir calorifique du carburant E 15 est de 46 × 103 kJ . kg–1, calculer le pourcentage massique
en éthanol du carburant.
-
Données :
-
Formule développée de l’éthanol :
-
PC (essence) = 48 × 103
kJ . kg–1
-
M (éthanol) = 46 g . mol–1 |
|
Composition du carburant E 15 : 1.
Équation de la réaction de combustion
complète de l’éthanol C2H6O
(ℓ).
2.
Estimer l’énergie molaire de combustion de
l’éthanol et en déduire le pouvoir calorifique de l’éthanol.
-
Énergie molaire de combustion Ecomb
de l’éthanol
-
Au cours de la combustion d’une mole
d’éthanol,
►
Les
liaisons rompues :
-
1
× 5 moles de liaisons
C – H
-
1
× 1 mole de liaisons C –
O
-
1
× 1 mole de liaisons H –
O
-
1
× 1 mole de liaisons C –
C
-
3
× 1 mole de liaison O = O
-
Eℓrompues =
5 × Eℓ (C –
H) + 1 × Eℓ
(C – O) + 1 × Eℓ
(O – H) +
1× Eℓ (C – C)
+ 3 × Eℓ (O = O)
-
Eℓrompues =
5 × 413 +
1
× 360 +
1 × 463 +
1
× 348 +
3 × 496
-
Eℓrompues ≈ 4,724
× 103 kJ . mol–1
-
Eℓrompues
≈ 4,72 × 103 kJ . mol–1
-
Au cours de la combustion d’une mole
d’éthanol,
►
Les liaisons formées :
-
2
× 2 moles de liaisons C = O
-
3
× 2 liaisons H – O
-
Eℓformées =
4 × Eℓ (C =
O) + 6 × Eℓ
(H – O)
-
Eℓformées =
4 × 796 +
6 × 463
-
Eℓformées
= 5,962
× 103 kJ . mol–1
-
Eℓformées
= 5,96 × 103 kJ . mol–1
-
Énergie molaire de combustion du
méthanol :
-
Ecomb (C2H6O)
= Eℓrompues – Eℓformées
-
Ecomb (C2H6O)
≈ 4,38 × 103 – 5,96 × 103
-
Ecomb (C2H6O)
≈ – 1,238
× 103 kJ . mol–1
-
Ecomb (C2H6O)
≈ – 1,24 × 103
kJ . mol–1
-
Pouvoir calorifique de l’éthanol :
-
Pouvoir calorifique
PC de l’éthanol :
-
Relation :
-
Application numérique :
-
3.
Pourcentage massique en éthanol du
carburant.
-
Pourcentage massique de l’éthanol :
P (éth)
-
Pourcentage massique de l’essence :
P (ess)
-
Avec :
-
P (éth) +
P (ess) = 100
-
On tire l’expression suivante :
-
P (ess) = 100 –
P (éth)
-
Le pouvoir calorifique du carburant
E 15 :
-
PC (E
15) = 46 × 103 kJ . kg–1
-
PC (éth) = 26,9 × 103
kJ . kg–1
-
PC (ess) = 48 × 103
kJ . kg–1
-
On peut écrire la relation suivante :
-
-
Application numérique :
-
|
|
|