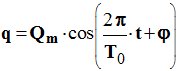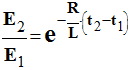|
Énoncé |
|
|
On étudie un oscillateur électrique idéal représenté figure ci-après :
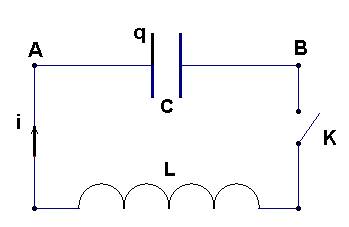 |
Il est constitué par : ► Un
condensateur de capacité C = 0,50 µF ► Une
bobine d’inductance L = 0.50 H ► La
résistance R du circuit est négligeable. On charge le condensateur, la tension à
ses bornes vaut : uAB (t
= 0) = U0 = 6,0 V. Puis, à la date t = 0, on ferme
l’interrupteur K. |
|
1)- Soit q la charge de l’armature
A du condensateur à
l’instant t quelconque (t > 0).
a)- Écrire l’expression de la tension aux
bornes du condensateur en fonction de q et
C. (
b)- Écrire l’expression de la tension aux
bornes de la bobine en fonction de q,
L
et
t. (
2)- Déduire de la question 1)- l’équation différentielle qui régit les
variations de la
charge q. (
3)- L’équation différentielle admet une solution de la forme :
a)- Que représentent les grandeurs
Qm et
T0
? ( b)- Le symbole φ représente la phase à l’origine des dates.
Vérifier que la valeur
φ = 0 est en accord avec
les conditions de l’étude. (
4)- Calculer la période propre des oscillations. ( |
II- Oscillateur réel. Document
|
On réalise l’expérience expérimentale d’un oscillateur électrique constitué par un condensateur de capacité C = 0,50 µF et une bobine d’inductance L = 0.50 H.
Soit R la résistance totale
du circuit.
À l’aide d’une carte d’acquisition reliée à un ordinateur et d’un
logiciel de traitement de données, on obtient le document suivant
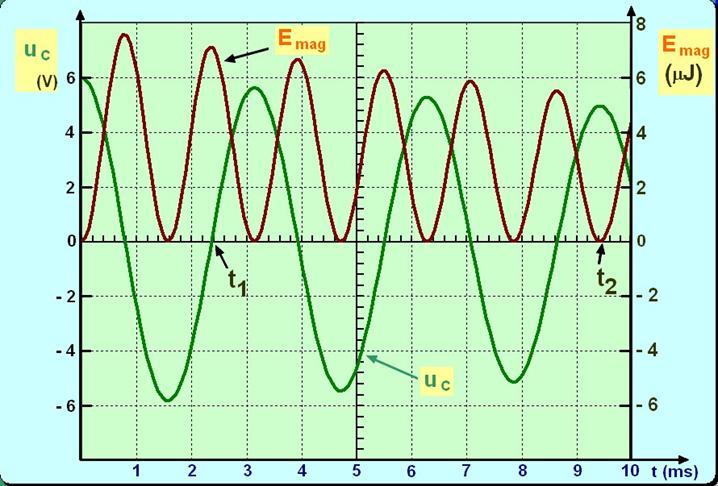
représentant :
- D’une part les variations de la tension uC
aux bornes du condensateur
en fonction du temps t : ordonnée
uC
axe gradué à gauche. - D’autre part les
variations de l’énergie Emag
emmagasinée dans la bobine en fonction du temps t : ordonnée
Emag
axe gradué à droite.
- Dans la suite, on notera Eelec
l’énergie emmagasinée dans le condensateur.
1)- Déterminer graphiquement la valeur de la pseudo-période
T des
oscillations. (
2)- Déduire du graphique la valeur de la charge portée par l’armature
A
du condensateur au temps t = 0. (
3)- Pour l’instant t
1 = 2,4 ms indiqué sur le document, déterminer à partir du graphique :
a)-
La valeur de l’énergie
E
1mag
emmagasinée dans la bobine à
l’instant
t1 ;
(
b)-
La valeur de l’énergie
E
1elec
emmagasinée dans le condensateur à
l’instant
t1
(justifier) ; (
c)-
La valeur de l’énergie électromagnétique
E
1
du circuit à l’instant
t1
(justifier) ; (
4)- Pour l’instant t
2 = 9,5 ms indiqué sur le document, déterminer à partir du graphique :
a)-
La valeur de l’énergie
E
2mag
emmagasinée dans la bobine à
l’instant
t2 ;
(
b)-
La valeur de l’énergie
E
2elec
emmagasinée dans le condensateur à
l’instant
t2
(justifier) ; (
c)-
La valeur de l’énergie électromagnétique
E2
du
circuit à l’instant t2
(justifier) ; ( 5)- À partir du graphe, justifier la conservation ou la non-conservation de l’énergie électromagnétique du circuit.
Quel phénomène physique explique
ces résultats ? (
6)- On admettra la relation |
Cliquer sur l'image pour l'agrandir