Controle N° 01 a , énoncé, Terminale S

Contrôle N° 01

Désintégration du carbone 14

Propriétés des désintégrations radioactives.

Temps de demi-vie et constante radioactive.

L'origine du radon.

La chimie au fil du temps.

Énoncé

Correction

1. Désintégration du carbone 14.

On donne Les numéros atomiques suivants : Z = 6 pour le carbone (C) et Z = 7 pour l’azote (N).

1.1. Pourquoi les noyaux de symboles et sont-ils appelés isotopes ?

1.2. Donner la composition du noyau de symbole

1.3. Le carbone 14 se désintègre en azote 14.

1.3.1. énoncer les lois de SODDY.

1.3.2. écrire l’équation de désintégration du carbone 14 en supposant que le noyau fils n’est pas obtenu dans un état excité.

Indiquer le type de radioactivité observé.

2. Propriétés des désintégrations radioactives.

2.1. Donner les caractéristiques des transformations radioactives en complétant les phrases du tableau suivant.

2.1.1.	La transformation radioactive d’un noyau possède un caractère …………………… ► Mots proposés : □ prévisible □ aléatoire □ périodique
2.1.2.	La désintégration d’un noyau …… ………….celle d’un noyau voisin ► Expressions proposées : □ n’affecte pas □ modifie □ est perturbée par
2.1.3.	Un noyau ‘’âgé’’ a ……… …….de se désintégrer qu’un noyau ‘’jeune’’. ► Expressions proposées : □ plus de chances □ moins de chances □ autant de chances
2.1.4.	L’évolution de la population d’un grand nombre de noyaux radioactifs possède un caractère ► Mots proposés : □ prévisible □ aléatoire □ périodique

2.2. Donner la loi de décroissance radioactive en précisant la signification et l’unité de chaque lettre.

3. Temps de demi-vie et constante radioactive.

3.1. Donner la définition du temps de demi-vie d’un échantillon radioactif que l’on notera t _½.

3.2. retrouver l’expression littérale de la durée de demi-vie en fonction de la constante radioactive à partir de la loi de décroissance : Justifier.

3.3. Le temps de demi-vie de l’isotope du carbone 14 est t _½ = 5,70 x 10³ ans.

En déduire la valeur de la constante radioactive λ en seconde (1 an = 365,25 j)

3.4. L’activité A (t) d’un échantillon radioactif à l’instant de date t est donnée ici par l’expression :

A (t) = λ . N (t).

3.4.1. Définir l’activité et donner son unité dans le système international.

3.4.2. En utilisant cette expression et la loi de décroissance, déduire que relation A (t) / A0 où A₀ représente l’activité à l’instant t₀ = 0 s.

3.4.3. Sachant qu’au temps t = 0 s, l’activité de l’échantillon est A₀ = 814 Bq.

Calculer le nombre N_o de noyaux radioactifs présents dans l’échantillon à cette date.

En déduire le nombre de noyaux N présents au bout d’une durée Δt = 5 t_½.

4. Origine du Radon.

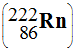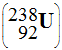Le radon 222 Rn222 est issu de la désintégration de l’uranium 238 U238 contenu dans les roches terrestre.

Calculer le nombre de désintégrations α et β^– nécessaires pour passer de l’uranium 238 au radon 222.

5. La chimie au fil du temps.

5.1. Demi-équations : il ne faut pas faire les choses à moitié.

Équilibrer les demi-équations d’oxydoréduction des couples oxydant / réducteur suivants

(le cas échéant, on supposera être en milieu acide H⁺).

5.1.1. Couple Ag⁺ _(aq) / Ag _(s).

5.1.2. Couple ClO^– _(aq) / Cl_{2 (aq)}.

5.2. Une réaction lente.

On réalise l’oxydation des ions iodure I^– _(aq) (du couple I₂ _(aq) / I^{^–}_(aq)) par

les ions peroxodisulfate S₂O₈^2– _(aq) (du couple S₂O₈^2– _(aq) / SO₄^2– _(aq)).

Pour ce faire, on mélange, à l’instant t = 0 s, un volume V₁ = 100 mL

d’une solution d’iodure de potassium de concentration C₁ = 0,25 mol / L

avec un volume V₂ = 100 mL d’une solution de peroxodisulfate de sodium de concentration :

C₂ = 2,0 x 10^{– 2} mol / L.

5.2.1. Écrire l’équation de la réaction d’oxydoréduction correspondante.

5.2.2. Calculer les quantités de matière de chacun des réactifs à l’instant initial.

5.2.3. Dresser le tableau d’avancement de la réaction et calculer la valeur de l’avancement maximal x_max.

5.2.4. Calculer la valeur de la concentration en diiode en fin de réaction.