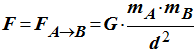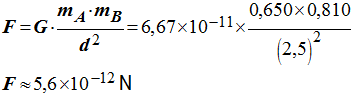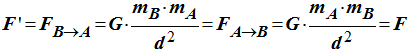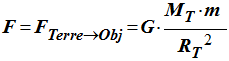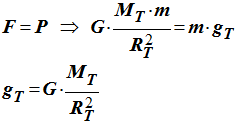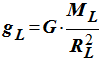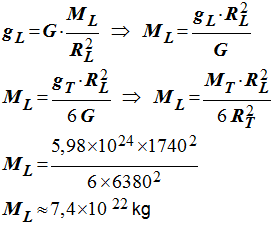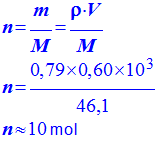I- Gravitation.

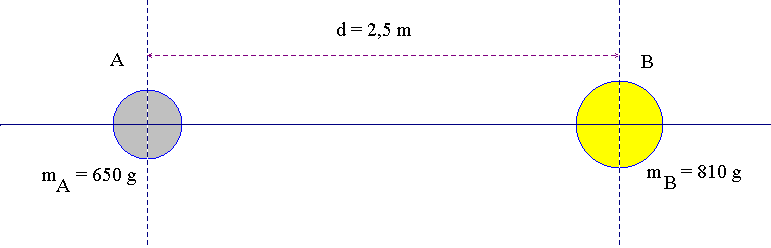
Deux boules de pétanques, l’une de centre A et de masse mA = 650 g, l’autre de centre B et de masse mB = 810 g, sont posées sur le sol. La distance entre leurs centres est d = 2,5 m. On donne : G = 6,67 x 10 – 11 m 3 . kg – 1 . s – 2 et g = 9,8 N / kg.   1)- Faire un schéma légendé de la situation - Schéma légendé de la situation : Cliquer sur l'image pour l'agrandir  2)- Donner l’expression de la force F de gravitation exercée par la boule A sur la boule B. - Expression de la force F de gravitation exercée par la boule A sur la boule B : -    3)- Calculer la valeur de la force F. -  Valeur de la force F : -   4)- La boule B exerce-t-elle une force de gravitation sur la boule A ? Si oui, donner la valeur F’ de cette force. -  Expression de la force F' de gravitation exercée par la boule B sur la boule A : -  Réciproquement, la boule B exerce une force sur la boule A : -

II- De la Terre à la Lune.

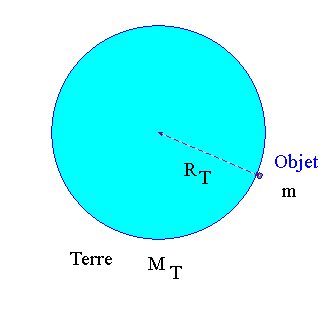
1)- Donner l’expression de la valeur de la force de gravitation F exercée par la Terre sur un objet de masse m posé sur le sol. On note : Masse de la Terre MT et rayon de la Terre RT. - Expression de la valeur de la force de gravitation F exercée par la Terre sur un objet de masse m posé sur le sol : - Schéma de la situation : -   2)- Donner l’expression du poids P de cet objet en fonction de sa masse m et de l’intensité gT  de la pesanteur terrestre. - P = m . g T 3)- Sachant que F = P, donner l’expression de gT en fonction de G, RT  et MT. -  Expression de gT : -    4)- Par analogie, en déduire l’expression de gL de l’intensité de la pesanteur à la surface de la Lune en fonction de G, RL  et ML. - Expression de gL : -      5)- L’intensité de la pesanteur à la surface de la Lune est six fois plus faible que l’intensité de la pesanteur à la surface de la Terre.  Calculer la masse de la Lune. - Masse de la Lune : -

 

III- Masse molaire, quantité de matière et volume.

 

1)- Calculer la masse molaire des corps purs suivants :  a)-  L’acide ascorbique (vitamine C) (C6H8O6). - Masse molaire de la molécule d’acide ascorbique : - M (C6H8O6) = 6 M (C) + 8 M (H) + 6 M (O) - M (C6H8O6) ≈ 176 g / mol b)-  La caféine : (C4H10O2N4). -  Masse molaire de la molécule de caféine : -  M (C4H10O2N4)  =  4 M (C) + 10 M (H) + 2 M (O) +  4 M (N) -  M (C4H10O2N 4) ≈ 146 g / mol c)-  Calculer la quantité de matière contenue dans m = 1,00 g de chacune de ces substances. -  Quantité de matière d’acide ascorbique : -  n (C6H8O6) = m (C6H8O6) / M (C6H8O6) -  n (C6H8O6) = 1,00 / 176 -  n (C6H8O6) ≈ 5,68 x 10 – 3  mol -  Quantité de matière de caféine : -  n (C4H10O2N4)  = m (C4H10 O2N4)  / M (C4H10O2N4) -  n (C4H10O2N4)  = 1,00 / 146 -  n (C4H10O2N4)  ≈  6,85 x 10 – 3  mol d)-  Calculer le nombre de molécules correspondant pour chaque substance. -  Nombre de molécules d’acide ascorbique : -  N (C6H8O6) = n (C6H8O6) . N A   -  N (C6H8O6) = 5,68 x 10 – 3  x 6,02 x 10 23 -  N(C6H8O6) ≈ 3,42 x 10 21 molécules -  Nombre de molécules de caféine : -  N (C4H10O2N4) = n (C4H10O2N4) .NA   -  N (C4H10O2N4)  = 6,85 x 10 – 3 x 6,02 x 10 23 -  N (C4H10O2N4) ≈ 4,12 x 10 21 molécules 2)- On remplit un flacon de volume V = 2,00 L de gaz diazote dans les conditions normales de température et de pression (CNTP). a)-  Calculer la quantité de matière n (N 2) de diazote contenu dans le flacon dans les CNTP. - Quantité de matière n (N 2) de diazote contenu dans le flacon dans les CNTP : - n (N2) = V / V m - n (N2) = 2,00 / 22,4 - n (N2) ≈ 8,93 x 10 – 2 mol b)-  Calculer la masse m (N2) de diazote contenu dans le flacon dans les CNTP. - Masse m (N2) de diazote contenu dans le flacon dans les CNTP : - m (N2) = n (N2) . M (N2) - m (N2) = 8,93 x 10 – 2  x 28,0 - m (N2) ≈ 2,50 g c)-  Calculer le volume occupé par cette quantité de matière à 20 ° C et sous la pression de 1013 hPa. Le volume molaire des gaz dans ces conditions est Vm = 24,4 L / mol. - Volume occupé par cette quantité de matière à 20 ° C et sous la pression de 1013 hPa - Vocc = n (N2) . V m - Vocc = 8,93 x 10 – 2  x 24,4 - Vocc = 2,18 L 3)- L’éthanol est un liquide de formule (C2H6O) et de masse volumique ρ = 0,79 g / cm 3. a)-  Calculer la masse molaire de l’éthanol. -  Masse molaire de l’éthanol : -  M (C2H6O) = 2 M (C) + 6 M (H) +  M (O) -  M (C2H6O) ≈ 46,1 g / mol b)-  Calculer la quantité de matière n d’éthanol contenue dans un volume V = 0,60 L d’éthanol. -  Quantité de matière d’éthanol : -