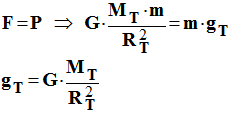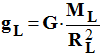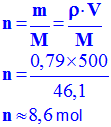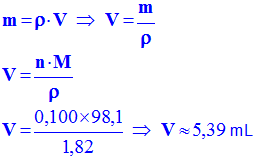1)- Donner l’expression de la valeur de la force de gravitation F exercée par

la Terre sur un objet de masse m posé sur le sol.

On note : Masse de la Terre M_T et rayon de la Terre R_T.

-  Expression de la force F :

-   

2)- Donner l’expression du poids P de cet objet en fonction de sa

masse  m et de l’intensité g_T  de la pesanteur terrestre.

-  Expression du poids P : 

-  P = m . g_T

3)- Sachant que F = P, donner l’expression de g _T en fonction de G, R_T  et M_T.

-  Expression de g _T :

-   

4)- Par analogie, en déduire l’expression de g_L de l’intensité de la pesanteur

à la surface de la Lune en fonction de G, R_L  et M_L.

-  Expression de g _L :

-   

5)- L’intensité de la pesanteur à la surface de la Lune est six fois plus faible

que l’intensité de la pesanteur à la surface de la Terre.

Calculer la masse de la Lune.

-  Masse de la Lune :

-   

On veut étudier l’influence de la longueur de L du pendule simple sur sa

période T afin de compléter l’étude de Galilée.

On utilise une sphère de cuivre de rayon R = 1,75 cm et de masse m = 100 g.

Les résultats sont consignés dans le tableau.

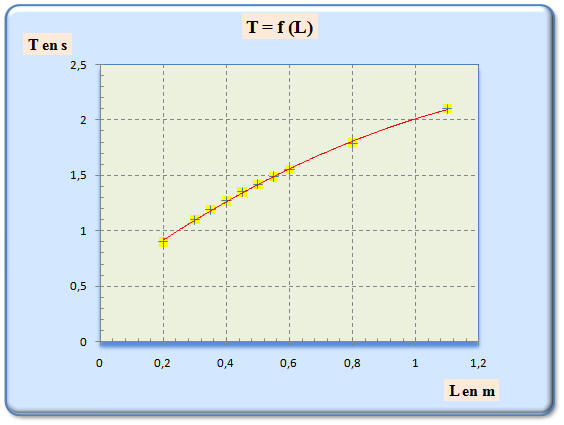
1)- Tracer la courbe représentant les variations de la période T en fonction de la longueur du pendule L.

- Tracé  de la courbe T = f (L):

2)- La période T est-elle proportionnelle à la longueur L du pendule ? Justifier.

-  Relation entre la période et la longueur du pendule :

-  La période T n’est pas proportionnelle à la longueur L du pendule car la courbe obtenue n’est pas une droite passant par l’origine.

-  Les points ne sont pas alignés.

3)- L’expérimentateur désire concevoir un pendule qui ‘’batte’’ la seconde, c’est-à-dire que le pendule change de sens exactement chaque seconde.

Utiliser la courbe précédente pour déterminer la longueur L du pendule. Justifier la réponse.

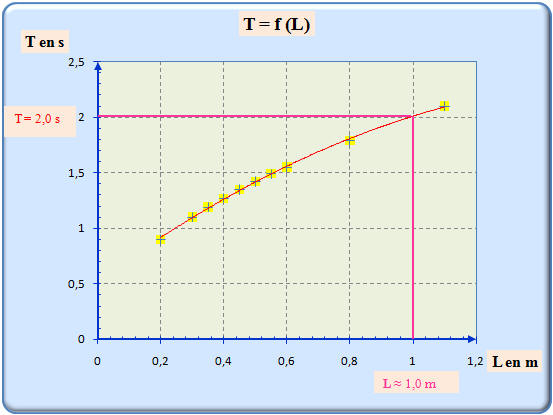
-  Le pendule qui bat la seconde a une période T = 2,0 s.

-  Graphiquement, à l’aide de la courbe, on peut déterminer la valeur de la longueur du pendule associé,

-  on trouve : L ≈ 1,0 m.

4)- Finalement, le pendule fabriqué par l’expérimentateur retarde.

Faut-il réduire ou augmenter la longueur L du pendule ?

Justifier la réponse.

-  Raccourcir ou allonger un pendule qui retarde :

-  Comme le pendule retarde, sa période T > 2,0 s.

-  En conséquence, il faut raccourcir le pendule car la période du pendule diminue lorsque la longueur du pendule diminue.

1)- Dans le sang, on trouve différentes substances.

En particulier, on recherche lors d’une analyse de sang, le glucose (C₆H₁₂O₆) et l’urée (CH₄N₂O).

a)- Calculer la masse molaire de ces molécules.

-  Masse molaire de la molécule de glucose :

-  M (C₆H₁₂O ₆) = 6 M (C) + 12 M (H) + 6 M (O)

-  M (C₆H₁₂O₆) ≈ 180 g / mol

-  Masse molaire de la molécule d’urée :

-  M (CH₄N₂O)  =  M (C) + 4 M (H) + 2 M (N) + M (O)

-  M (CH₄N₂O) ≈ 60,0 g / mol

b)- Calculer la quantité de matière contenue dans m = 1,00 g de chacune de ces substances.

-  Quantité de matière de glucose :

-  n (C₆H₁₂O₆) = m (C₆H₁₂O₆) / M (C₆H₁₂O₆) 

-  n (C₆H₁₂O₆) = 1,00 / 180

-  n (C₆H₁₂O₆) ≈ 5,56 x 10 ^{– 3}  mol

-  Quantité de matière d’urée :

-  n (CH₄N₂O)  = m (CH₄N₂O)  / M (CH₄N₂O) 

-  n (CH₄N₂O)  = 1,00 / 60,0

-  n (CH₄N₂O)  ≈  1,67 x  10 ^{– 2}  mol

c)- Calculer le nombre de molécules correspondant pour chaque substance.

-  Nombre de molécules de glucose :

-  N (C₆H₁₂O₆) = n (C₆H₁₂O₆) .N_A  

-  N (C₆H₁₂O₆) = 5,56 x  10 ^{– 3}  x  6,02 x 10 ²³

-  N (C₆H₁₂O₆) ≈ 3,34 x  10 ²¹ molécules

-  Nombre de molécules d’urée :

-  N (CH₄N₂O)  = n (CH₄N₂O) . N_A  

-  N (CH₄N₂O)  = 1,67 x  10 ^{– 2}  x  6,02 x  10 ²³

-  N (CH₄N₂O) ≈ 1,00 x  10 ²² molécules

2)- L’éthanol est un liquide de formule (C₂H₆O) et de masse volumique

ρ = 0,79 g / cm ³.

a)-   Calculer la masse molaire de l’éthanol.

-  Masse molaire de l’éthanol :

-  M (C₂H₆O) = 2 M (C) + 6 M (H) + M (O)

-  M (C₂H₆O) ≈ 46,1 g / mol

b)- Calculer la quantité de matière n d’éthanol contenue dans un volume

V = 0,50 L d’éthanol.

-  Quantité de matière d’éthanol :

-   

3)- La masse volumique de l’acide sulfurique (H₂SO₄) est ρ = 1,82 g / cm ³.

Quel volume d’acide sulfurique liquide faut-il prélever

pour obtenir 0,100 mol d’acide sulfurique ?

Décrire le mode opératoire pour prélever cette solution.

-  Volume d’acide sulfurique nécessaire :

-   

-  Il faut utiliser les gants et les lunettes car le produit est corrosif.

-  On verse la solution mère dans un bécher.

-  On prélève 10 mL de la solution à l’aide d’une pipette graduée de 10 mL munie de sa propipette.

-  On en verse la quantité nécessaire, ici V =  5,4 mL dans le récipient.

-  On vide la pipette graduée dans le bécher et on la nettoie.