I- But.

-  Exploitation avec un tableur d’une série de mesures. Utilisation d’un tableau de mesures, tracé de graphes et recherche d’un modèle.

II- Exemple de tableur : Excel.

1)- Présentation d’un tableur.

► Un tableur est un logiciel performant qui permet :

-  De construire et de modifier des tableaux : ensemble de lignes et de colonnes.

-  De faire des calculs variés sur les lignes et les colonnes de ces tableaux.

-  De construire des graphiques à partir des données de ces tableaux.

-  …..

► C’est un outil très utilisé pour exploiter les résultats expérimentaux en Sciences physiques.

2)- Ouverture d’Excel.

a)-     Présentation.

►       L’écran comprend :

-  La barre de titre (nom du logiciel avec le nom du fichier) : 1.

-  La barre de menu (Fichier, Édition,…..) : 2.

-  La barre des outils standards : 3.

-  La barre des outils mise en forme : 4.

-  La barre de formule : 5.

-  La barre d’état : 6.

b)-    La feuille de calcul :

► La feuille de calcul est divisée en cellules, intersection de lignes et de colonnes.

-  Une feuille de calcul Excel contient 256 colonnes (A à IV) et 65536 lignes (1 à 65536).

-  Les colonnes sont repérées par des lettres : de A à Z pour les 26 premières et de combinaisons de deux lettres pour les autres.

-  Les lignes sont indiquées par des numéros de 1 à 65536.

-  Une cellule est caractérisée par sa colonne et sa ligne : la cellule C2.

c)-     Les cellules.

► Lors de l’ouverture d’une nouvelle feuille de calcul, toutes les cellules sont vides.

► Une cellule peut contenir :

-  Une donnée numérique : la cellule A2 contient la valeur numérique 1.

-  Une formule, formée du signe égal suivi d’une expression littérale : la cellule C2 contient la formule : =A2+B2^2.

-  Que représente cette formule ?

-  Un texte indiquant par exemple une grandeur et son unité.

III- Tracé de graphes et exploitation.

1)- Le problème posé.

► Le but est de donner différentes représentations graphiques, de les analyser et de tirer une loi physique.

2)- Le tableau de valeurs.

-  Ouvrir une nouvelle feuille Excel.

-  Reproduire et compléter le tableau suivant avec les mesures que vous avez effectuées.

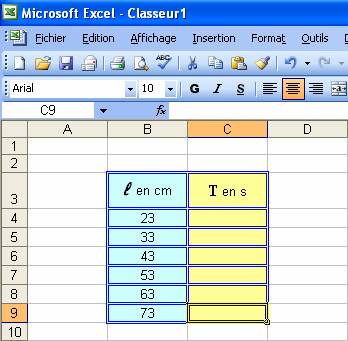
3)- Représentation graphique.

-  À l’aide de la souris (clic gauche), sélectionner la plage de cellules : B4:C9.

-  sur l’icône , puis comme type de graphique, choisir , Nuage de points et comme sous-type de graphique,

-  Sélectionner le premier en haut à gauche.

-  sur Suivant, sélectionner série en colonnes et 8 sur suivant.

-  Titre du graphique : T = f (ℓ)

-  Axe des abscisses (X) : ℓ  en cm

-  Axe des ordonnées (Y) :  T  en s

-  sur Axes : cocher : axes des abscisses (X) et choisir : automatique puis cocher : axe des ordonnées (Y).

-  sur  Quadrillage : cocher quadrillage principal pour l’axe des abscisses et l’axe des ordonnées.

-  sur Suivant et sur Terminer.

-  En sélectionnant le graphe, on peut agir sur la hauteur ou la largeur en tirant sur les poignées.

-  sur l’axe des abscisses. sur Motifs. Cocher : Graduation principale : Extérieure ;

-  Graduation secondaire : intérieure ; étiquette de graduation : En bas, puis  sur O.K.

-  sur l’axe des ordonnées. sur Motifs. Cocher : Graduation principale : Extérieure ;

-  Graduation secondaire : intérieure ; étiquette de graduation : En bas, puis  sur O.K.

-  sur la Zone de traçage et sélectionner la couleur : jaune clair puis  sur O.K.

-  sur la Zone de graphique et sélectionner la couleur : vert clair puis  sur O.K.

-  sur la série des ordonnées : Format de la série de données : Marques : cocher Personnalisée ;

-  Premier plan : bleu, arrière plan : bleu ciel ; Style + puis  sur O.K..

-  Sélectionner : Titre de l’axe des ordonnées, sur Format, titre de l’axe sélectionné,

-  sur Alignement puis régler l’angle sur 0 °,

-  puis  sur O.K.

-  On peut déplacer les différents textes du graphique.

4)- Exploitation des valeurs.

-  Commenter le graphe obtenu. Quelles sont les remarques que l’on peut faire ?

5)- Applications.

-  Le but est de représenter les graphes suivants, de les interpréter et de modéliser.

a)-     Représenter le graphe : en respectant les unités suivantes T en seconde s et ℓ en mètre m.

-  Remarque : Excel peut calculer la racine d’un nombre situé dans une cellule : = racine(cellule).

-  Exploitation : Quelles sont les remarques que l’on peut faire ?

► À partir du graphe, on peut retrouver la relation liant et T.

-  sur graphique et sur Ajouter courbe de tendance.

-  Type : linéaire ;

-  Options : cocher : Afficher l’équation sur le graphique et

-  Afficher le coefficient de détermination (R²) sur le graphique, puis  sur O.K.

Interpréter le résultat obtenu :

-  Excel donne l’équation de la représentation graphique obtenue grâce à une étude statistique.

-  Le coefficient de détermination permet de savoir si le modèle utilisé est en adéquation avec la représentation graphique obtenue.

-  Lorsque R² = 1, l’adéquation est parfaite.

-  Si R² ≈ 1, il y a une dépendance statistique entre les variables x et y.

-  C’est souvent le cas en physique car on travaille avec des valeurs expérimentales.

-  Le but est de trouver un modèle mathématique qui se rapproche le plus du modèle expérimental.

-  Le coefficient de détermination R² permet de savoir si le modèle choisi est bien en accord avec les résultats expérimentaux.

-  En déduire la relation liant et T.

b)-    Représenter le graphe : T² = f (ℓ) en respectant les unités suivantes T en seconde s et ℓ  en mètre m.

-  Formule pour élever un nombre au carré : = cellule ^ 2 (combinaison de touche)

Quelles sont les caractéristiques de la courbe obtenue ?

Exploiter le graphe avec Excel. Donner l’expression mathématique de la relation entre T² et ℓ.

Comparer le résultat obtenu avec celui trouvé avec le tracé sur papier millimétré. Conclusions.