I- Définitions.

II- Étude expérimentale.

1)- Dispositif expérimental.

Il comprend : une source lumineuse, un disque qui permet la mesure des différents angles, un demi-disque en Plexiglas. 

- Faire le schéma du dispositif expérimental.

2)- Mesures.

- On fait varier l’angle d’incidence i₁ en tournant le disque et pour chaque valeur de  i₂, on note les valeurs, de l’angle de réflexion r de l’angle de réfraction  i₂.

Reproduire et compléter le tableau suivant : 

Cliquer sur l'image pour l'agrandir

 Animation CabriJava pour réaliser les mesures.

Vidéo de la série de mesures.

III- Exploitation des mesures.

1)- Hypothèses.

Depuis l’Antiquité, de nombreux savants se sont penchés sur le phénomène de réfraction. 

Ils ont cherché à établir la loi physique reliant les angles  i₁ et  i₂.

a)- Pour Ptolémée (Grec 200 ans AV JC) :

- Soient i₁ et  i'₁ deux angles d’incidence et,  i₂ et  i'₂ les angles de réfraction correspondants.

- Si i₁ > i'₁  alors  i₂ > i’₂ .

b)- Pour Grosseteste (Anglais 12 ^ième – 13 ^ième siècle).

- 

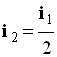
c)- Pour Kepler (Allemand 15 ^ième – 16 ^ième siècle).

-  i₁ = k . i₂

d)- Pour Descartes (Français) et Snell (Hollandais) (16 ^ième – 17 ^ième siècle). 

- sin i₁ = k . sin i₂

2)- Questions.

a)- Tester la validité des hypothèses précédentes à l’aide de quelques valeurs du tableau.

b)- Graphe  :  sin i₁ = k . sin i₂.

Tracer la courbe sin i₁ = k . sin i₂.

- Calculer le coefficient directeur k de la droite moyenne. Donner son unité.

- En déduire la relation liant sin i₁ et  sin i₂.

- Conclusions : Donner la loi de la réfraction.

3)- Interprétation.

L’indice de réfraction n :  

- Relation : 

- Remarque : n_vide ≈ n_air ≈ 1,0

- Le coefficient k est égal au quotient de n₂, indice de réfraction du milieu 2 (le Plexiglas) par n₁, indice de réfraction du milieu 1 (l’air). 

- En conséquence : 

En déduire la valeur du coefficient de réfraction du Plexiglas.

  Le Plexiglas est-il plus réfringent que l’air ?

IV- Application 1. (Si le temps le permet).

1)- Passage du milieu 1 (l’air) au milieu 2 (le Plexiglas).

- Remarque : le milieu 1 (l’air) est moins réfringent que le milieu 2 (le Plexiglas).

Comparer les valeurs de i₁ et i₂ lorsque la lumière passe du milieu 1 (l’air) au milieu 2 (le Plexiglas).

- Quelle est la valeur prise par  i₂ lorsque i₁= 90 ° ?

2)- Passage du milieu 1 (le Plexiglas) au milieu 2 (l’air).

- Il suffit pour passer du milieu 1 (le Plexiglas) au milieu 2 (l’air) de tourner le demi-disque de Plexiglas de 180°.

- Ainsi, le rayon lumineux traverse d’abord le milieu 1 (le Plexiglas) puis le milieu 2 (l’air).

- Remarque : le milieu 1 (le Plexiglas) est plus réfringent que le milieu 2 (l’air).

Comparer les valeurs de i₁ et i₂ lorsque la lumière passe du milieu 2 (le Plexiglas) au milieu 1 (l’air).

- Que se passe-t-il lorsque l’angle i₂ devient trop grand ?

- En déduire la valeur limite i_lim qui permet la réflexion totale du rayon lumineux.

a)- L’indice de réfraction :  

- Relation : 

- Remarque : n_vide ≈ n_air ≈ 1,0

- Le coefficient k est égal au quotient de n₂, indice de réfraction du milieu 2 (le Plexiglas) par n₁, indice de réfraction du milieu 1 (l’air). 

- En conséquence : 

En déduire la valeur du coefficient de réfraction du Plexiglas.

-  Le Plexiglas est-il plus réfringent que l’air ?