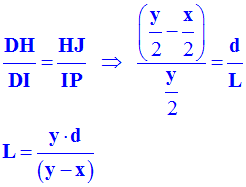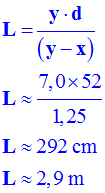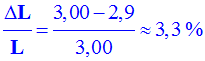|
TP Physique N° 03 |
La Visée : Vous visez quoi ? Comment ? pourquoi faire ? Enoncé. |
|
|
|
Programme 2010 : Physique et Chimie Programme 2020 : Physique et Chimie |
|
|
|
objectif : déterminer la distance d’un objet inaccessible par mesure directe. |
|
II- Mesure du rayon de la Terre. 2)- La mesure du rayon de la Terre |
Matériel : Double décimètre, feuille de papier.
![]() À l’aide d’une règle transparente posée verticalement
contre la vitre et maintenue à bout de
bras,
À l’aide d’une règle transparente posée verticalement
contre la vitre et maintenue à bout de
bras,
- mesurer avec un œil (O) la hauteur apparente h du campanile de la porte Soubeyran.
- Durant cette mesure, l’autre membre du binôme, avec un mètre d’arpenteur ou un réglet, mesure la distance d entre l’œil (O) et le repère inférieur de la longueur h.
|
À l’aide d’une règle transparente tenue verticalement et maintenue à bout de bras, mesurer avec un œil (O) la hauteur apparente h du support posé sur la paillasse
du professeur.
|

![]() Faire le schéma de la manipulation.
Faire le schéma de la manipulation.
- Présenter les résultats des différentes mesures sous forme d’un tableau.
![]() Énoncer le principe de propagation rectiligne de la lumière.
Énoncer le principe de propagation rectiligne de la lumière.
- Comment se nomme la ligne droite concernée ? Comment est-elle orientée ?
- À l’aide du théorème de Thalès, exprimer littéralement D puis déterminer sa valeur numérique.
- Vérifier le résultat à l'aide du mètre ruban.
- Dans quels domaines cette méthode peut-elle être utilisée ?
II-
Mesure du rayon de
|
Avec son invasion en 332 avant J.C. par Alexandre le Grand, l'Égypte va vivre pendant trois siècles son influence grecque. Pendant cette période, Parmi tous les savants de l'époque, on distinguera :
Aristarque de Samos.
Il émet
l’hypothèse que
(notamment la
forme du cône d’ombre sur Ératosthène. Directeur de la grande bibliothèque d'Alexandrie en 236 avant J.C., il eut accès à l'ensemble du savoir de son temps.
En 205 avant J.C, il propose une méthode
purement géométrique pour mesurer la taille de Ératosthène observa que les ombres ne sont pas les mêmes suivant l'endroit où l'on se trouve. En particulier, il compara les ombres le jour du solstice d'été dans
deux villes : Syène (Assouan) au sud et Alexandrie au nord. A Syène (ASSOUAN), à midi, le Soleil est au zénith. Cela signifie que les objets n'ont pas d'ombre. Ératosthène observa que les rayons du Soleil atteignent
verticalement le fond d'un puits. Le même jour, à la même heure, à Alexandrie, plus au nord, les bâtiments ont une ombre. Ératosthène constate que la longueur de l’ombre faite par un gnomon (tige verticale qui servait de cadran solaire) représente le 1/8 de la
hauteur de ce dernier.
Connaissant
approximativement la distance entre les deux villes, Ératosthène en
déduisit la circonférence de
Comme
lui, nous allons en déduire le rayon de |
2)-
La mesure du rayon de
- Ératosthène fit l’hypothèse selon laquelle les rayons du soleil arrivant sur Terre sont parallèles entre eux.
- Comment justifier cette hypothèse ?
|
|
- Reproduire le schéma ci-contre (rayon du cercle R = 10) cm. - Placer les villes de Syène (S) et d’Alexandrie (A), connaissant leur latitude : - 24° Nord pour Syène et 31°Nord pour Alexandrie. - Ératosthène considère que ces deux villes sont sur le même méridien.
- Sur
le schéma, représenter en pointillé, en partant du centre de
- Placer,
à Alexandrie, un gnomon à la verticale du lieu de longueur
h =
(échelle non respectée
par rapport à - Tracer la direction des rayons du Soleil à Syène, le jour du solstice d’été à midi et au même moment à Alexandrie. - Dessiner puis mesurer l’ombre du gnomon. - On notera ℓ cette longueur. |
Document 1 :
- Soit α l’angle formé par les deux verticales et β l’angle formé par le gnomon à Alexandrie et les rayons du soleil.
- Les représenter sur le schéma.
- Quelle relation existe-t-il entre ces deux angles.
- Comme le Soleil est très éloigné de la Terre, on considère que les rayons solaires sont parallèles.
- On en déduit que α = β.
- Calculer β en utilisant les relations trigonométriques dans un triangle rectangle et en déduire la valeur de α.
- On travaille dans le triangle ABC rectangle en A :
-
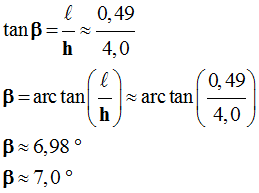
- Les relevés cadastraux de l’époque d’Ératosthène indiquaient 5000 stades pour la distance entre Syène et Alexandrie.
-
Sachant que 1 stade =
- Distance d entre ces deux villes en mètres :
- d = 5000 x 157
-
d
≈ 7,85
x
10
- Vérifier la valeur trouvée à l’aide de la carte fournie (document 1). Conclusion.
- Distance trouvée à l'aide du plan :
- Mesure avec Photofiltre : Mesure 1
- Utilisation de l'échelle : Mesure 2
|
|
Sur la carte |
En réalité |
|
Distances |
5,08 cm |
200 km |
|
Alexandrie – Assouan |
20,02 cm |
d |
- Distance dp sur le plan :
-

- On remarque que dp ≈ d
- L'incertitude relative sur la valeur de d :
-
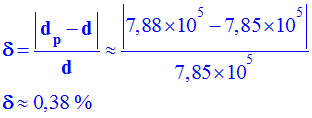
-
Connaissant l’angle
α et la distance
d séparant les deux villes, en déduire
la circonférence de
|
Angle α |
7,0 ° |
360 ° |
|
Distance |
7,85
x
10 5 m |
p |
- Circonférence de la Terre :
-
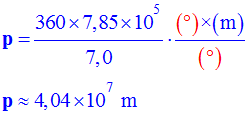
- En
déduire la valeur du rayon
RE
de
ʘ
- Valeur du rayon de la Terre :
-
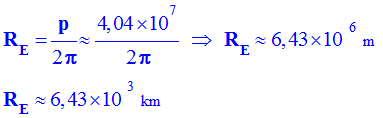
-
Comparer cette valeur avec celle actuellement admise de
- Déterminer la valeur de l’incertitude relative
 sur
la mesure.
sur
la mesure.
-
Incertitude
relative :
- - Conclusion.
- Cette
méthode permet de trouver le rayon de la Terre avec une bonne précision (de
l'ordre de 1 %).
III-
Parallaxe entre les yeux
(Pour aller plus loin)
-
Le phénomène de parallaxe se manifeste quand on vise un objet
de 2 endroits différents.
- La
parallaxe est l’angle
p entre deux directions de visée du point
qui représente l’objet.
-
Viser avec l’œil gauche (G) le point fixe
P et l’aligner avec la graduation zéro
(O) du double décimètre
tenu horizontalement à bout de bras.
- Sans bouger la tête, viser avec l’œil droit (D) le point fixe
P et mémoriser la
division
x de la graduation coïncidant
avec
P.
-
L’autre membre du binôme mesure la distance
y entre les deux yeux
et la distance
d
entre le point I
et le point
P'.
-
Mesure des distances d et
L
et
AB
: L 300 cm d 52,0 cm y 7,00 cm x 5,75 cm
- Schéma :
ʘ
I est le milieu du
segment
GD et (PI)
// (JH)
Étudier
les triangles
HDJ
et IDP. Utiliser le théorème de Thalès
et exprimer
HD
en fonction de
y et
x.
- À quoi peut-on s’attendre si le
point P est à plus de 20 m ? Que constate-t-on ? Que peut-on
dire des rayons ? - Relation : - Les droites
(HJ) et
(IP)
sont parallèles. -
Le théorème de Thalès appliqué à la figure permet
d'écrire la relation suivante : - On étudie les triangles
HDJ
et IDP :
-
- Résultat obtenu : -
-
Précision de la mesure :
-
- Si le point
P est très éloigné, plus de 20
mètres, alors : x
≈
y. - Les rayons lumineux
(GP) et
(DP)
sont pratiquement parallèles. -
Les rayons lumineux qui arrivent dans les
yeux d'un observateur en provenance d'un objet éloigné sont quasiment
parallèles. 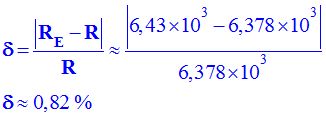
![]() Choisir un point fixe
P
situé à plus de 2 m.
Choisir un point fixe
P
situé à plus de 2 m.![]() Indiquer
les différentes mesures.
Indiquer
les différentes mesures.
![]() Faire un schéma et retrouver la relation suivante :
Faire un schéma et retrouver la relation suivante :



![]() Comparer
le résultat obtenu avec sa mesure.
Comparer
le résultat obtenu avec sa mesure.