|
Phys. N° 06 |
La Gravitation Universelle. Cours. |
|
|
Programme 2010 : Programme 2010 : Programme 2020 : |
|
|
|
|
|
II- L’interaction gravitationnelle. |
|
III-
Trajectoire
d’un projectile dans
un référentiel terrestre. |
|
|
|
|
|
|
|
Exercices 2005-2006 Physique et Chimie seconde Collection DURANDEAU HaCHETTE |
|
|
1)- Exercice 2 page 116. |
4)- Exercice 7 page 116 |
|
2)- Exercice 4 page 116 |
5)- Exercice 9 page 117 |
|
3)- Exercice 6 page 116 |
6)- Exercice 17 page 118 |
|
Physique et Chimie seconde Collection Microméga Hatier Ancienne édition |
|
|
1)- Exercice 12 page 253. |
2)- Exercice 15 page 253 |
|
3)- Exercice 18 page 254 |
4)- Exercice 20 page 254 |
Pour aller plus loin :
|
Logiciel pour la simulation en mécanique (lancer de projectiles mise sur orbite de satellites) et pour l'exploitation de vidéos (chronophotographie) |
Gratuit |
|
Mots clés : Gravitation Universelle ; Le mouvement de la Lune ; l'interaction gravitationnelle ; trajectoire d'un projectile ; mouvement des satellites ; le satellite géostationnaire ; le poids sur la Lune ; le référentiel géocentrique ; poids et force gravitationnelle ; ... |
I-
Le
mouvement de la Lune.
![]()
1)- Le mouvement de la Lune pour un observateur terrestre.
- Pour un observateur terrestre, la Lune se lève à Est et se couche à l’Ouest.
- La trajectoire de la Lune dans le ciel change d’un jour à l’autre.
- Le mouvement de la Lune par rapport à la Terre est complexe.
- Le référentiel terrestre n’est pas adapté pour l’étude du mouvement de la Lune.
- On préfère utiliser le référentiel Géocentrique.
2)- Le référentiel Géocentrique.
- Le référentiel Géocentrique est un solide constitué par le centre de la Terre et des étoiles lointaines dont les positions n’ont pas varié depuis des siècles.
- Le référentiel Géocentrique n’est par entraîné dans le mouvement de rotation de la Terre.
- Le principe de l’inertie s’applique dans le référentiel Géocentrique.
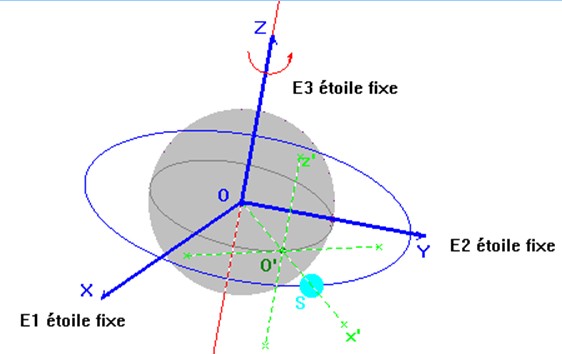
- L’origine du repère lié au référentiel Géocentrique est
située au centre de
-
- On peut choisir l’étoile polaire.
- Les axes x’Ox et y’Oy sont situés dans le plan équatorial et ils sont orientés vers des étoiles lointaines supposées fixes.
- Ce référentiel est commode pour l’étude des satellites de
-
- Dans
ce référentiel,
- Dans le référentiel Géocentrique, la trajectoire de la Lune est pratiquement un cercle de rayon R = 384 000 km.
- Soit 60 fois le rayon de la Terre.
- La durée d’un tour que l’on appelle la période sidérale est de 27,3 jours.
Cliquer sur l'image pour l'agrandir
4)- Cause du mouvement de la Lune.
- Si la Lune n’était soumise à aucune force, d’après le principe de l’inertie, elle serait animée d’un mouvement rectiligne uniforme dans le référentiel géocentrique.
- En conséquence, la Lune est soumise au moins à une force.
- Tournant autour de la Terre, on peut en déduire que la Lune est soumise à une force exercée par la Terre.
- La force exercée par la Terre sur la Lune est une force d’origine gravitationnelle.
II-
L’interaction
gravitationnelle.
![]()
1)- La Loi de Gravitation universelle.
|
Énoncé : - Deux corps ponctuels, de masses m et m’, séparés par une distance d, exercent l’un sur l’autre des forces attractives, de même valeur :
- - G est appelé la constante de gravitation universelle : - G ≈ 6,67 × 10 – 11 m 3 . kg – 1 . s – 2- Valeur de la force F en Newton N. - Valeur des masses m et m’ en kg. - Distance séparant les deux masses ponctuelles : d en m |
Schéma :

- Les forces se représentent par des flèches, appelées vecteurs, de même longueur , de même direction , mais de sens opposés.
- Ce résultat se généralise à des corps à répartition sphérique de masse.
- La masse est répartie de façon régulière autour du centre de corps.
- C’est le cas de la Terre, de la Lune, des planètes et des étoiles.
- Dans le cas de l’interaction gravitationnelle entre la Terre et la Lune, la valeur de la force exercée par la Terre sur la Lune est donnée par l’expression :
- 
- M T : masse de la Terre : M T = 5,98 × 1024 kg.
- M L : masse de la Lune : M L = 7,34 × 1022 kg.
- d : distance entre le centre de la Terre et le centre de la Lune : d = 384 000 km.
- Calculer la valeur de F.
- 
- Schéma :

- Cette force F retient la Lune sur son orbite autour de la Terre.
- Cette force du à l’interaction gravitationnelle est une force
attractive représentée par le vecteur ![]() , appliqué au centre de la Lune et dirigé
vers le centre de la Terre.
, appliqué au centre de la Lune et dirigé
vers le centre de la Terre.
3)- Poids et force gravitationnelle.
a)- Le poids.
- Sur la terre, Tout corps de masse m est soumis à une force appelée poids du corps :
- Expression du poids : P = m.g.
- P poids en Newton N, m la masse en kg et g le facteur d’attraction terrestre : g = 9,8 N / kg.
b)- La force gravitationnelle.- D’autre part, ce corps de masse m est soumis à une force gravitationnelle de la part de la Terre.
- ![]()
- Si l’objet est situé à la surface de la Terre, on peut considérer que :
- d = RT = 6380 km.
c)- Comparaison de F et de P.
- ![]() .
.
- Il faut comparer :
-
![]()
- calculer l’expression :
- 
- Le poids d’un objet sur Terre est pratiquement égal à la force gravitationnelle exercée par la Terre sur l’objet.
- Remarque :
- La différence entre le poids d’un objet sur la Terre et la force de gravitation exercée par la Terre sur l’objet provient de la rotation de la Terre sur elle-même.
- Le poids d’un corps peut s’identifier à la force gravitationnelle exercée par la Terre sur l’objet.
- La valeur du poids varie en fonction de la latitude et de l’altitude.
d)- Poids d’un corps sur la Terre et sur la Lune.
- Un corps de masse m n’a pas le même poids sur la Terre que sur la Lune.
- Un objet de masse m est environ six fois plus léger sur la Lune que sur la Terre.
- Comment peut-on retrouver ce résultat ?
- ![]()
- Il faut connaître le rayon de la Lune et la masse de la Lune.
- RL = 1,75 × 10 6 m et ML = 7,34 × 10 22 kg
- 
- ![]()
III-
Trajectoire
d’un projectile dans un référentiel terrestre.
![]()
- Expérience du tube de Newton.
- Un corps est en chute libre s’il n’est soumis qu’à son poids.
- Le mouvement des corps en chute libre est indépendant de sa masse.
- Expérience de la feuille de papier que l’on plie.
- Dans l’air, la trajectoire particulière d’une plume est due aux forces exercées par l’air sur la plume.
- On peut considérer qu’une bille de faible dimension n’est soumise qu’à son poids.
- Elle est en chute libre dans l’air car on peut négliger la résistance de l’air sur un petit trajet.
2)- Influence de la vitesse initiale.
- Considérons une bille lancée avec une vitesse initiale.
- On peut considérer qu’elle n’est soumise qu’à son poids.
- On va étudier l’influence de la vitesse initiale de la bille sur la trajectoire.
- Pour cela, on utilise une animation CabriJava pour simuler la situation.
![]() Plaçons-nous dans
le cas ou la bille est lancée horizontalement et faisons varier la valeur de
la vitesse.
Plaçons-nous dans
le cas ou la bille est lancée horizontalement et faisons varier la valeur de
la vitesse.
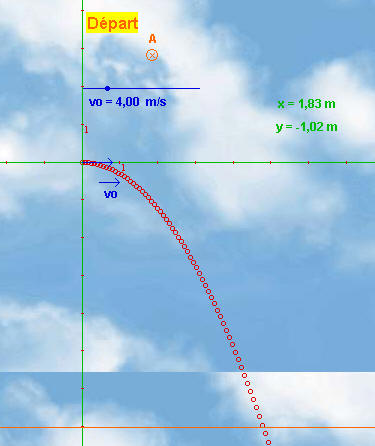
Lancer d'un projective avec vitesse initiale horizontale
- Qu’elles sont les remarques que l’on peut faire ?
- Plus la valeur de la vitesse initiale est grande et plus le point de chute est éloigné.
![]() On modifie
la direction du lancement tout en gardant la même valeur pour la vitesse.
On modifie
la direction du lancement tout en gardant la même valeur pour la vitesse.
- Lancer d'un projectile avec une vitesse initiale faisant un angle α avec l'horizontale.
Vidéo : billec.avi

Animation : CABRIJAVA

- On note α l’angle que fait la direction de la vitesse avec l’horizontale.
- On peut prendre α = 30 °, 45 °, 60 °, .
- On remarque que la distance de chute est la même pour les angles de 30 ° et 60° mais que la hauteur est différente.
- La distance de chute est maximale pour l’angle de 45 °.
- En conclusion :
- La trajectoire d’un projectile en chute libre dépend de la valeur de la vitesse et de la direction de lancement.
- La vitesse selon la direction horizontale (perpendiculaire au poids) est constante.
- Le mouvement horizontal est uniforme.
- La vitesse selon la verticale (direction du poids) varie.
- Le mouvement vertical n’est pas uniforme, il est varié.
Animation : CABRIJAVA mouvement parabolique

- Pour aller plus loin :
IV-
Mouvement
de la Lune et des satellites.
![]()
1)- Le lancement d’un Satellite.
- Comment faut-il faire pour lancer un satellite artificiel de la Terre ?
- On peut imaginer comme l'a fait Newton qu’on lance une pierre du sommet d’une montagne.
- Si on la lance horizontalement et de plus en plus vite, elle va tomber de plus en plus loin.
- Si sa vitesse est suffisamment grande et en négligeant la résistance de l’air, on peut penser que la trajectoire repassera par son point de départ.
- La pierre ne tombe plus sur la Terre elle est satellisée.
- C’est le cas de la Lune.
2)- Pourquoi la Lune ne tombe-t-elle pas sur la Terre ?
- La Lune attirée par la Terre ne tombe pas sur sa surface car elle possède une vitesse suffisante pour être satellisée.
- La valeur de la vitesse de la Lune ne change pas au cours du temps. Elle est constante.
- Mais la direction de son mouvement change à chaque instant.
- La trajectoire s’incurve. La Lune est soumise à une force attractive exercée par la Terre sur la Lune.
- Cette force change de direction à chaque instant : c’est une force centripète.
- Elle est toujours dirigée vers le centre de la Terre.

|
Exercices 2005-2006 Physique et Chimie seconde Collection DURANDEAU HaCHETTE |
|
|
1)- Exercice 2 page 116. |
4)- Exercice 7 page 116 |
|
2)- Exercice 4 page 116 |
5)- Exercice 9 page 117 |
|
3)- Exercice 6 page 116 |
6)- Exercice 17 page 118 |
|
Physique et Chimie seconde Collection Microméga Hatier Ancienne édition |
|
|
1)- Exercice 12 page 253. |
2)- Exercice 15 page 253 |
|
3)- Exercice 18 page 254 |
4)- Exercice 20 page 254 |