I- Objectifs

II- Expérience assistée par ordinateur.

1)- Données :

- Masse du mobile : m = 536 g

- Raideur du ressort : k = 10 N.m^-1

- Intervalle de temps : τ =

2)- Réalisation de l'enregistrement.

- Décrire brièvement l'expérience et faire un schéma du dispositif expérimental (vue de dessus et vue de profil).

III- Étude à l'ordinateur.

1)- Protocole opératoire.

- Mettre l'ordinateur sous tension. Cliquer sur l'icône diginum 4.

- Faire un enregistrement à l'ordinateur central.

- Enregistrer le fichier de mesures dans le dossier TSV_ (donner un nom du type OSC...).

- Charger les mesures sur votre ordinateur (fichier - ouvrir - réseau - …)

2)- Étude de y = f (x).

- Représenter à l'écran les variations de y en fonction de x.

- Cette courbe est-elle exploitable ? Peut-on en déduire une caractéristique du mouvement de G ?

3)- Étude de y = f (t) .

- Cliquer sur l'icône Échelle / Graphe

- mettre t en abscisse, y en ordonnée 1.

- Que peut-on dire du mouvement de G ?

- Mesurer la période T.

- Mesurer l'amplitude y_m  des oscillations. Quelle remarque peut-on faire ?

- Recherche de la relation : y = f (t) ;

- On choisit comme solution :

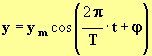
- On connaît les valeurs de y_m  et de T, il reste à calculer la valeur de φ.

- Pour φ, on peut effectuer une recherche par tâtonnement (faire une itération) à l'aide de l'ordinateur puis une recherche théorique (φ est lié aux conditions initiales).

- Détermination de φ.

Méthode 1 : à l'aide du réticule ou du tableau de valeurs on détermine l'ordonnée y₀ à l'instant initial et l'amplitude du mouvement y_m.

Exemple :

On utilise l'ordonnée à l'origine

On utilise la vitesse à l'origine

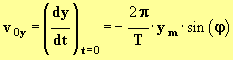
Or  v_0y > 0  car le mobile se déplace de y' vers y.

En conséquence :

 Méthode 2 : à l'aide du réticule , on détermine la date t qui correspond au passage du mobile à l'élongation maximale pour la première fois.

Exemple :

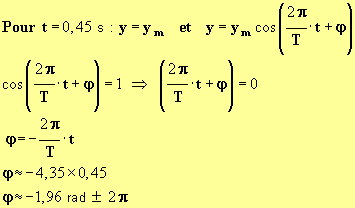
- Vérifier que les points expérimentaux sont sur la courbe 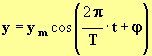à l'aide de l'ordinateur.

- Dans le menu Traitements,

- choisir Tracé de fonctions et donner à chaque paramètre la valeur expérimentale.

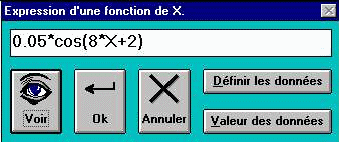
- Taper l'expression en donnant à chaque paramètre la valeur expérimentale et remplacer t par X.

- Puis cliquer sur Voir.

- Exemple :

4)- Étude de la vitesse v_y = g (t).

- Représenter à l'écran les variations de v_y en fonction du temps t.

- Cliquer sur l'icône Échelle / Graphe

- mettre t en abscisse, v_y en ordonnée 1

- Mesurer la période T . En déduire la pulsation ω. Mesurer l'amplitude v_m des oscillations

- Montrer dans un premier temps que .

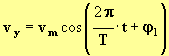- puis que .

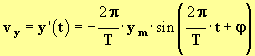- Représenter y (t) et v_y (t) simultanément à l'écran. Quelles remarques peut-on faire ?

5)- Étude de l'accélération a_y = h (y).

- Représenter à l'écran a _y  en fonction de y.

- Cliquer sur l'icône Échelle / Graphe,

- mettre a_y  en abscisse, y en ordonnée 1

- Quelles sont les caractéristiques de la courbe obtenue ?

- Faire un ajustement linéaire en cliquant sur l'icône .

- En déduire l'équation de la courbe obtenue. Comparer la valeur du coefficient directeur p à ω ² .

- En déduire que a_y = y'' (t) . Donner l'expression de a_y  en fonction du temps.

II- Étude énergétique.

1)- Énergie potentielle élastique.

- L'énergie potentielle élastique d'un ressort de raideur k est donnée par la relation :

2)- Énergie cinétique.

- L'énergie cinétique est donnée par la relation :

3)- Énergie mécanique.

- L'énergie mécanique du système est donnée par la relation : E_t = E_C + E_P

On ne tient pas compte de l'énergie potentielle de pesanteur car le mobile se déplace sur une surface plane et horizontale. 

En conséquence, l'énergie potentielle de pesanteur ne varie pas au cours du mouvement du mobile. 

On choisit comme origine des altitudes la position initiale du mobile.

4)- Travail à faire.

- Faire tracer à l'ordinateur, pour une demi-période, les courbes E_C, E_P et E_t en fonction du temps t .

- Cliquer sur l'icône Échelle / Graphe,

- mettre t en abscisse, E_C en ordonnée 1, E_P en ordonnée 2, E_t en ordonnée 3

- Observations. Conclusions.

III- Application.

1)- Étude d'un point.

- Déterminer, l'ordonnée y_i, la date t_i, la vitesse v_i et l'accélération a_i du point d'indice i.

- Donner les caractéristiques du vecteur vitesse et du vecteur accélération.

2)- Étude dynamique.

- Étudier le système à l'équilibre (bilan des forces) sachant que les deux ressorts, de raideurs respectives k₁ et k₂ sont tendus. 

- En déduire la condition nécessaire à l'équilibre. Il est recommandé de faire un schéma.

- Étudier le système en mouvement. Représenter le système à l'instant t quelconque. 

- Déterminer l'équation différentielle du mouvement à l'aide du théorème du centre d'inertie (2° Loi de Newton).

Animation :