I- Expérience et enregistrement.

1)- Décrire le dispositif utilisé informatique et mécanique.

-  Partie mécanique : on utilise un plan incliné  d’un angle a = 10 ° (environ)et un mobile autoporteur de masse m = 0,536 kg.

-  Partie informatique : on utilise une table à digitaliser munie de son stylet. 

-  Le logiciel DIGINUM 4 permet l’étude du mouvement du mobile. 

-  La table à digitaliser permet de repérer la position d’un point particulier du mobile à intervalle de temps τ.

-  Dans le cas présent : τ = 44,25 ms

-  L’imprimante permet d’obtenir un enregistrement à l’échelle 1.

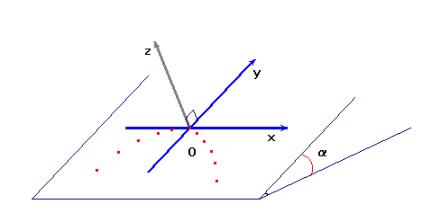
2)- Décrire l'expérience et faire des schémas du dispositif (vue de dessus et de profil).

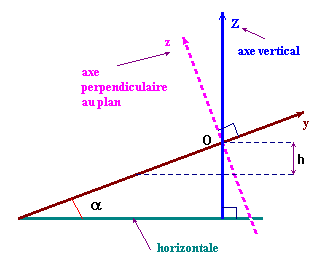
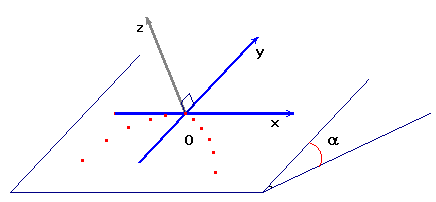
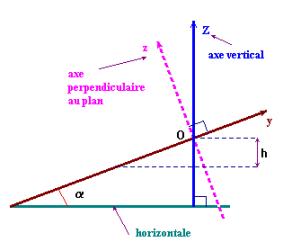
II- Repère d'espace et repère de temps.

1)- Introduction.

L'ordinateur impose le repère d'espace : .

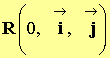On travaille en vraie grandeur. 

L'ordinateur enregistre la position du stylet à intervalles de temps régulier τ.

Cet intervalle de temps est donné par l'ordinateur.

l'ordinateur choisit comme origine des dates, l'instant ou la position du point mobile coïncide avec l'origine des espaces O. 

Le point O correspond au sommet de la trajectoire du point mobile. noter  la valeur de tau : τ  = 44,25 ms

Enregistrement : 

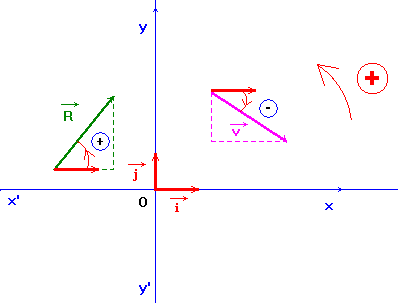
2)- Coordonnées cartésiennes d'un vecteur.

--  Pour connaître les coordonnées cartésiennes d'un vecteur, on projette ce vecteur sur les axes Ox et Oy.

-  

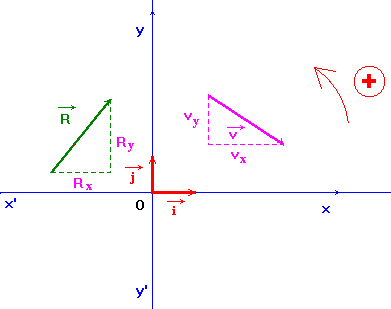
-  Remarque : R_x et R_y sont des grandeurs algébriques.

3)- Le vecteur vitesse.

-  Détermination de la valeur de la vitesse instantanée.

-  Soit i  =  l'indice du point choisi :

-  Les instants t_i–1 et t _i+1 encadrent l'instant t_i.

-  Tableau récapitulatif.

Mesurer la distance parcourue par le mobile : G_{i – 1} G_{i + 1}.

-  Déterminer la durée de parcours Δt.

-  En déduire la valeur de la vitesse v_Gi.

Tracé du vecteur vitesse.

-  Tracer la parallèle issue du point G_i à la droite (G_{i – 1} G_{i + 1}).

-  Donner la longueur du représentant ℓ_vi du vecteur vitesse. 

-  On utilise l'échelle : 0,1 m / s  ↔  1 cm.

-  Idem pour le point d’indice j.

Déterminer les coordonnées cartésiennes de chaque vecteur vitesse. vérifier les valeurs à l'aide de l'ordinateur.

-  Voir les valeurs du tableau au-dessus.

III- Force et variation de vitesse.

1)- bilan des forces extérieures appliquées un solide.

Faire le bilan des forces extérieures appliquées au solide.

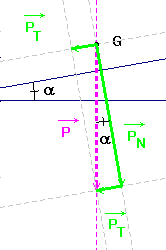
-  Faire un schéma de profil de la situation.

-  schéma de profil de la situation.

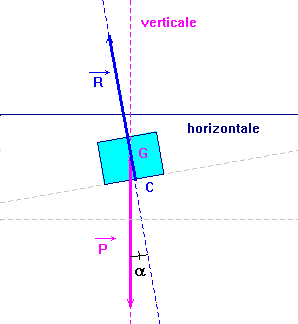
-  Représenter les actions mécaniques à partir du point G. On considère que les frottements sont négligeables.

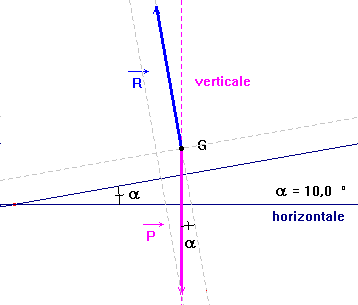
-  Décomposer les actions mécaniques suivant la perpendiculaire au plan incliné et la ligne de plus grande pente du plan incliné.

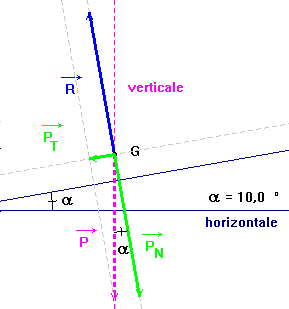
-  Le mouvement a lieu dans le plan incliné, en conséquence, la somme vectorielle des composantes perpendiculaires au plan incliné est nulle. 

-  

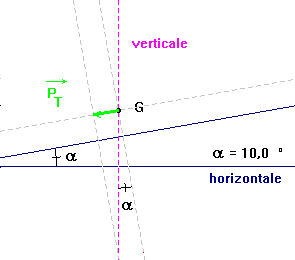
-  Tout se passe comme si le mobile n'était soumis qu'à la seule force   

-  En déduire les caractéristiques de la résultante : 

-  Direction : ligne de plus grande pente du plan incliné ; sens ; orienté vers le bas ; valeur :

-  F_R = m g sin a.

-   .

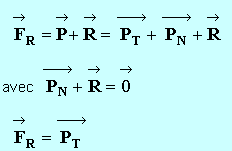-  Donner les coordonnées de  dans le repère :

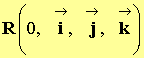
-  Relations :

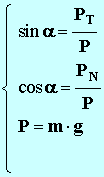
-  coordonnées du vecteur résultante des forces : 

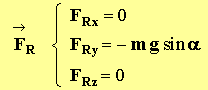
2)- Vecteur variation du vecteur vitesse de G aux temps t₅ et t₁₄.

-  Pour t₅ :

-  Rechercher les valeurs de v_{i –1} et v_{i + 1}  à l'aide de l'ordinateur.

Tracer le vecteur  à partir du point G_i.

-  Que représente ce vecteur ? 

-  Que peut-on dire du vecteur variation du vecteur vitesse de G et de la résultante  des forces extérieures ?

-  Pour t₁₄ : Idem.

-  Pour t₅ :

-  L’ordinateur donne : v₄  ≈ 0,54 m / s et v₆  ≈ 0,39 m / s

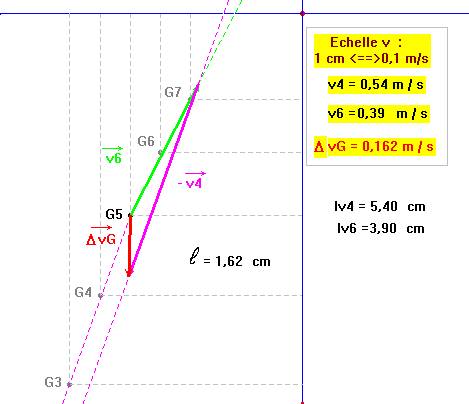
-  Le vecteur  représente la variation du vecteur vitesse pendant un intervalle de temps très court de 2 τ.

-  Il a même direction et même sens que la résultante  des forces extérieures.

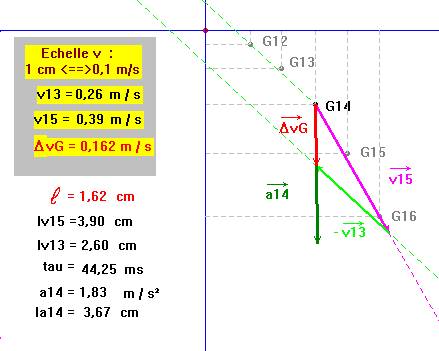
-  Pour t₁₄ :

-  L’ordinateur donne : v₁₃  ≈ 0,26 m / s et v₁₅  ≈ 0,39 m / s

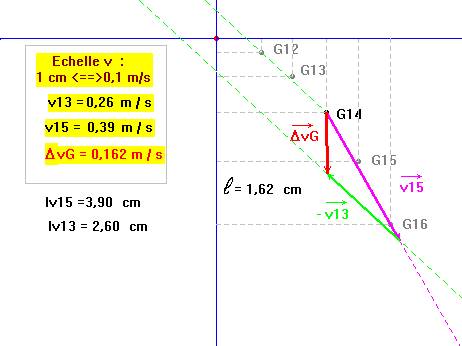
-  Le vecteur  représente la variation du vecteur vitesse pendant un intervalle de temps très court de 2 τ.

-  Il a même direction et même sens que la résultante  des forces extérieures.

IV- Le vecteur accélération.

1)- Introduction.

2)- Détermination de la direction et du sens du vecteur accélération aux temps t₅ et t₁₄.

-  Rechercher les valeurs de v _{i – 1} et v _{i + 1} à l'aide de l'ordinateur.

Tracer le représentant du vecteur à partir du point G_i.

-  Le vecteur accélération a même direction et même sens que le vecteur

3)- Détermination de la valeur a _i du vecteur accélération au temps t  _i.

Mesurer la longueur du représentant de .

-  À l'aide de l'échelle, donner la valeur de Δv_G en m / s.

-  Diviser Δv_G par  Δt  = 2 τ et en  déduire la valeur de l'accélération a_i. Attention aux unités.

-  En quelle unité s’exprime la valeur de l’accélération ?

-  La valeur de Δv_G en m / s :

-  Δv_G  ≈ 0,162 m / s.

-  La valeur de l'accélération a _i :

- 

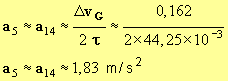
-  La valeur de l’accélération s’exprime en m / s ².

4)- Tracer le vecteur  Échelle : 1 m / s²  ↔ 2 cm.

-  Longueur du représentant : ℓ_a  ≈ 3,66 cm.

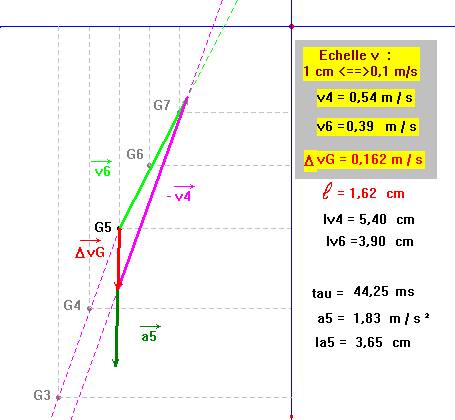
Déterminer les coordonnées cartésiennes du vecteur accélération.

-  Conclusion.

-    

- 

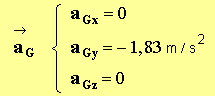
-  Il existe un écart entre la valeur expérimentale de l’accélération et la valeur théorique.

-  Cela provient de la précision sur la valeur de l’angle α.

-  De plus, il est préférable de faire un traitement statistique de l'ensemble des valeurs de l'accélération.

-  On peut remarquer que le vecteur accélération est pratiquement le même au cours du temps.

-  Conclusion :

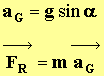
V- Équation des différentes courbes. (si le temps le permet)

1)- équations horaires des coordonnées du vecteur accélération.

-  Étudier les fonctions a_x = f₂ (t) et a_y = g₂ (t).

-  Cliquer sur l'icône  échelle / GRAPHE, mettre t en abscisse, a_x en ordonnée 1 et a_y en ordonnée 2.

-  Faire un traitement statistique (icône ajustement) et donner les relations : a_x = f₂ (t) et a_y = g₂ (t).

-  Lors du traitement statistique, il faut choisir l'intervalle afin d'éliminer les valeurs extrêmes dont le calcul est faux.

-   Coordonnées du vecteur accélération.

-  On travaille dans le repère 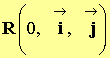car le mouvement du mobile se fait sur le plan incliné :

2)- Équations horaires des coordonnées du vecteur vitesse :  v_x = f₁ (t) et v _y = g₁ (t).

-  Idem.

-   Coordonnées du vecteur vitesse.

3)- Équations horaires des coordonnées du vecteur position : x = f (t) et y = g (t).

-  Idem. Donner l'équation de la trajectoire du point mobile.

-   Coordonnées du vecteur position

Équation de la trajectoire du point mobile.

-   Équation de la trajectoire :  y ≈ – 23,8 x²

-   On peut retrouver ce résultat en exprimant t en fonction de x dans l’expression suivante :

-   x ≈ 0,19 × t => t ≈ (x / 0,19)

-   On remplace dans l’expression de l’ordonnée y :

-   y ≈ – 0,86 × t² => y ≈ – 0,86 × (x / 0,19)²

-   y ≈ – 23,8 × x²