I- But

-  Créer des oscillations dans un circuit R.L.C. Mettre en évidence l’amortissement des oscillations.

II- Le logiciel

- Ouverture du logiciel et paramétrages.

- Démarrer CASSY Lab, activer les voies UA₁ et UB₁.

- Paramètres de mesure : intervalle entre deux mesures 20 µs – nombre de points : 400

- Cocher la case déclenchement et sélectionner la voie UA1 – valeur : 7,0 V et sens descendant.

III- Expérience.

1)- Montage :

-  Vérifier les valeurs des résistances à l’ohmmètre.

- Réaliser le montage, le faire vérifier et raccorder à la carte CASSY Lab (voies UA₁ et UB₁)

- Les composants : bobine : L = 46 mH et r = 8,5 Ω, une boîte de condensateurs et un conducteur ohmique R’ = 18 Ω.

- Réglage de la valeur de la capacité du condensateur :

- Pour commencer, régler la boîte de condensateurs C = 0,50 μF.

2)- Questions préliminaires :

-  Quelle tension visualise-t-on à la voie UA1 ? À la voie UB1 ?

3)- Acquisition :

- Régler la valeur de la tension aux bornes du générateur : E = 10,0 V

- Première étape : Basculer l’interrupteur sur la position 1 pour charger le condensateur.

- Deuxième étape : Réaliser l’acquisition en basculant rapidement l’interrupteur sur la position 2.

- Quel phénomène met-on en évidence ?

IV- Exploitation et Mesures.

1)- Étude quantitative de la courbe : u _AM  = g (t).

-  Visualisation de u_AM = g (t) :

- Adapter les échelles pour une meilleure exploitation des mesures

- Que représente la courbe obtenue ? Expliquer qualitativement cette courbe.

- Déterminer la valeur de la pseudo-période T du phénomène observé.

 2)- Étude de la courbe : i_exp = h (t).

- Créer la nouvelle grandeur i_exp = h (t).

- Visualisation de la courbe : i_exp = h (t). Adapter les échelles pour une meilleure exploitation des mesures

- Expliquer qualitativement cette courbe. Déterminer la valeur de la pseudo-période T du phénomène observé.

- Comparer avec la valeur précédente. Conclusion.

- La courbe rouge représente les variations de l’intensité dans le circuit en fonction du temps : iexp = h (t). - L’amplitude de l’intensité diminue au cours du temps et change de signe. - Le condensateur se décharge, puis se charge.  - Le phénomène est pseudo-périodique. - On trouve la même valeur que précédemment. - Il y a un décalage entre les deux courbes. - Elles sont en quadrature de phase. - Lorsque l’une des courbes est extrémale, l’autre est nulle.

V- Étude énergétique.

1)- Représenter sur un même graphique les variations :

- De l’énergie aux bornes du condensateur,

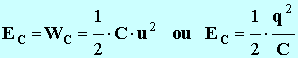
- De l’énergie aux bornes de la bobine,

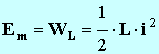
- De l’énergie totale du circuit : E_T = E_m  +  E_c 

-  Pour ce faire créer les nouvelles grandeurs correspondantes ? (Prendre 7 décimales)

Commenter les courbes obtenues.

- Pourquoi l’énergie totale diminue-t-elle au cours du temps ?

- Lorsque l’énergie emmagasinée par le condensateur atteint une valeur maximale, que peut-on dire de la valeur prise par l’énergie emmagasinée par la bobine ? Et inversement ?

- Déterminer au temps t = 0 s, la valeur de l’énergie totale dans le circuit, la valeur de l’énergie emmagasinée dans la bobine et la valeur de l’énergie emmagasinée dans le condensateur.

- Recommencer pour t = 1,0 ms. Quelles remarques peut-on faire ?

2)- Si le temps le permet :

a)-  Déterminer la valeur de la pseudo-période T’ de E_c ou E_L et comparer à la pseudo-période T trouvée au

IV- 1)-

- Refaire l’acquisition pour différentes valeurs de C et compléter le tableau suivant :

?Commenter les résultats du tableau. Comparer T et T₀. Montrer que . Conclusions.