I- Charge d’un condensateur par un courant d’intensité constante.

1)- But :

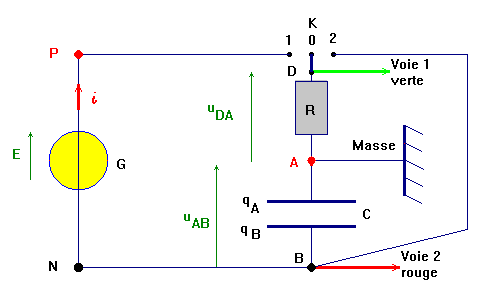
2)- Montage :

-  Le générateur de courant est constitué de la boîte blanche reliée au générateur de tension.

-  L’association délivre une intensité constante I₀.

Réglages : régler la tension aux bornes du générateur de tension U ≈  5,00 V.

-  Décharger le condensateur en reliant les bornes A et B par un fil, l’interrupteur K étant en position 0.

3)- Le Logiciel CONDO.

-  Dans le Fichier Physique, Lancer le Logiciel CONDO  puis appuyer sur une touche.

a)- Sélectionner : � CONNEXION :

-  Relier le point D à la voie 1 (borne verte), le point B à la voie 2 (borne rouge) et le point A à la masse (borne noire) de la carte CANDIBUS

b)- Sélectionner : (2) Paramètres : 

c)- Sélectionner : (3)Acquisitions : choisir �  : U = f (t) c’est-à-dire : u_AB = f (t).

-  Appuyer sur la lettre L de lancer et fermer l’interrupteur.

-  Lorsque l’acquisition est terminée, appuyer sur la lettre M pour revenir au menu précédent.

4)- Exploitation : étude des différentes courbes :  sélectionner (4)

a)- Étude de u_AB = f (t) : sélectionner : �

-  Commenter la courbe obtenue.

-  Donner ses caractéristiques. 

-  Donner la valeur de la tension U aux bornes du condensateur lorsqu’il est chargé. 

-  (on peut utiliser l’outil : POINTEUR)

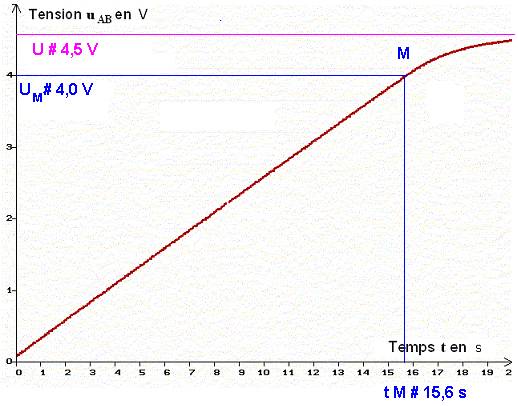
-  La courbe u_AB = f (t)  est pratiquement une droite qui passe par l’origine pour t compris entre 0 et 16 s environ.

-  Pour t > 16 s,  la courbe tend vers une asymptote horizontale.

-  u_AB = = a . t  

-  Détermination de la valeur du coefficient directeur a :

-  

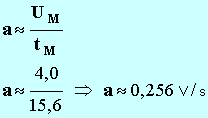
-  Valeur de la tension lorsque le condensateur est chargé : U ≈ 4,5 V.

b)- Étude de q_A = g (t) : sélectionner : (2)

-  Commenter la courbe obtenue. Donner ses caractéristiques. 

-  En déduire une relation simple entre q_A et t.  

-  (on peut utiliser l’outil : courbe de régression et choisir le modèle adapté). 

-  Que représente le rapport : .

-  Donner la valeur de la charge Q aux bornes du condensateur lorsqu’il est chargé. 

-  (on peut utiliser l’outil : POINTEUR) 

-  Que se passe-t-il lorsque le condensateur est chargé ?

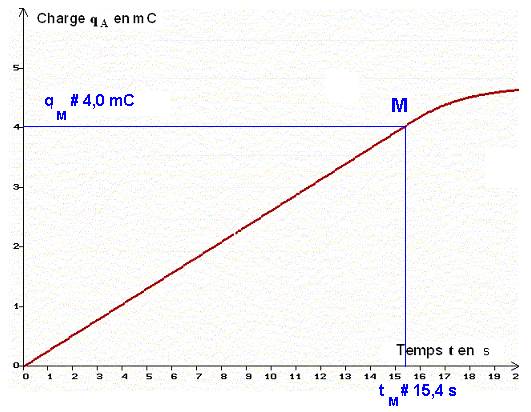
-  La courbe q_A = g (t)  est pratiquement une droite qui passe par l’origine pour t compris entre 0 et 16 s environ.

-  Pour t > 16 s,  la courbe tend vers une asymptote horizontale.

-  q_A = a . t  

-   

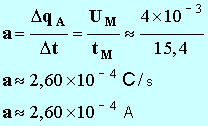
-  Le rapport  donne la valeur de l’intensité du courant constant délivré par le générateur de courant :

- 

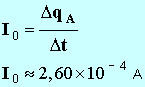
-  Charge du condensateur lorsqu’il est chargé.

-  Lorsque le condensateur est chargé, Q ≈ 4,5 mC.

-  La courbe tend vers une asymptote horizontale et l’intensité du courant dans le circuit tend vers zéro, elle s ‘annule.

c)-     Étude de q_A = h (u_AB) : sélectionner : ƒ

-  Commenter la courbe obtenue. Donner ses caractéristiques. 

-  Quelle conclusion peut-on tirer ?  En déduire une relation simple entre q_A et u_AB. 

-  (on peut utiliser l’outil : courbe de régression et choisir le modèle adapté).

-  Le coefficient trouvé représente la capacité C du condensateur, exprimée en farad (F). 

-  Comparer la valeur trouvée à celle donnée par le constructeur.

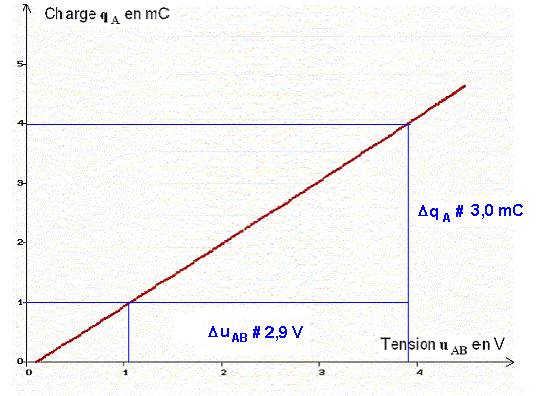
-  La courbe q_A = h (u_AB) est pratiquement une droite qui passe par l’origine.

-  On peut écrire que q_A = a . u_AB 

-  Détermination de la valeur de la constante a :

-  

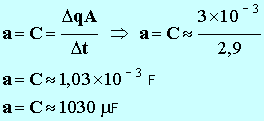
-  Le constructeur annonce une capacité de 1000 µF.

-  

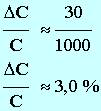
d)-     Étude de i = h (t) : sélectionner : „

-  Commenter la courbe obtenue. Donner ses caractéristiques. 

-  En déduire la valeur de I₀. 

-  Comparer cette valeur à  trouvée au b)-.

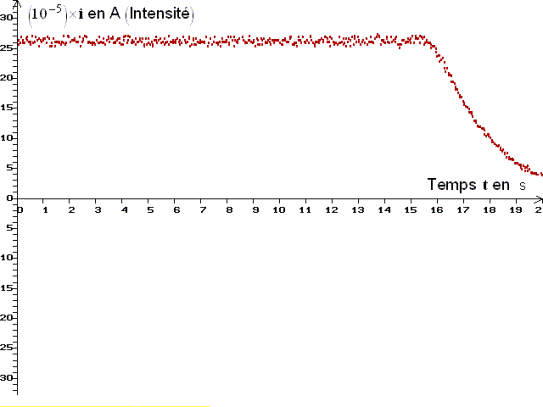
-  Lors de la charge, l’intensité du courant est constante et I₀ ≈ 26 x 10 ^{– 5}  A   ⇒    I₀ ≈ 2,6 x 10 ^{– 4}  A.

-  Lorsque le condensateur est chargé, l’intensité du courant dans le circuit diminue pour s’annuler.

-  Cette valeur est en accord avec celle trouvée à la question b)-.

II- Charge d’un condensateur par un échelon de tension.

1)- But :

2)- Échelon de tension

-  Un échelon de tension E est le passage instantané d'une tension de valeur nulle à une tension de valeur constante E.

-  Représentation :

3)- Montage :

 réaliser le montage suivant : le montage est le même que le précédent.

Réglages : régler la tension aux bornes du générateur de tension : U = E  ≈ 4,00 V.

-  Décharger le condensateur en reliant les bornes A et B par un fil, l’interrupteur K étant en position 0.

4)- Le Logiciel CONDO.

a)-     Sélectionner : � CONNEXION :

-  Relier le point D à la voie 1 (borne verte), le point B à la voie 2 (borne rouge) et le point A à la masse (borne noire) de la carte CANDIBUS.

b)-     Sélectionner : ‚ Paramètres :

c)-     Sélectionner : (3)  Acquisitions : choisir �  : U = f (t) c’est-à-dire : u_AB = f (t).

-  Cliquer sur la lettre L de lancer et fermer l’interrupteur.

-  Lorsque l’acquisition est terminée, appuyer sur la lettre M pour revenir au menu précédent.

5)- Exploitation : étude des différentes courbes :  sélectionner (4)

a)- Étude de q_A = h (u_AB) : sélectionner : (3)

-  Commenter la courbe obtenue. Donner ses caractéristiques. 

-  Quelle conclusion peut-on tirer ?  En déduire une relation simple entre q_A et u_AB. 

-  (on peut utiliser l’outil : courbe de régression et choisir le modèle adapté).

-  Le coefficient trouvé représente la capacité C du condensateur exprimée en farad (F). 

-  Comparer la valeur trouvée à celle donnée par le constructeur.

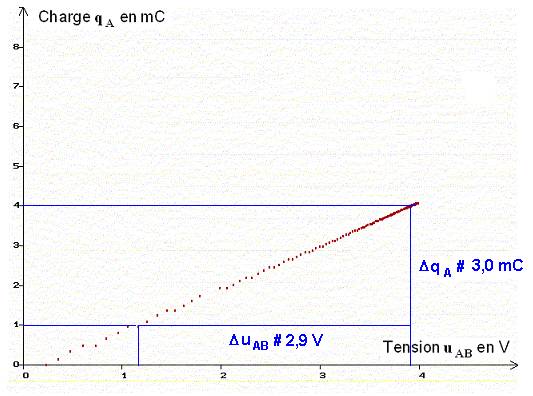
-  La courbe q_A = h (u_AB) est pratiquement une droite qui passe pratiquement par l’origine. 

-  Il y a un décalage qui provient probablement de la synchronisation au départ de l’acquisition.

-  On peut écrire que q_A = a . u_AB 

-  Détermination de la valeur de la constante a :

-  

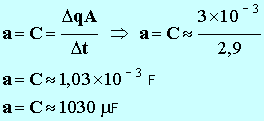
-  Le constructeur annonce une capacité de 1000 μF.

-  

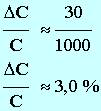
-  La capacité du condensateur  a = C  ≈ 1030 μF

b)-     Étude de u_AB = f (t) : sélectionner : �

-  Commenter la courbe obtenue. Donner ses caractéristiques. 

-  Donner la valeur de la tension U aux bornes du condensateur lorsqu’il est chargé. 

-  (on peut utiliser l’outil : POINTEUR)

-  Déterminer la durée nécessaire τ₁ pour que : .

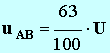-  Sur la courbe, tracer la tangente au point d’abscisse 0 et l’asymptote horizontale. 

-  Déterminer l’abscisse τ₂  de leur point d’intersection.

-  Comparer τ₁ et τ₂ au produit R.C.

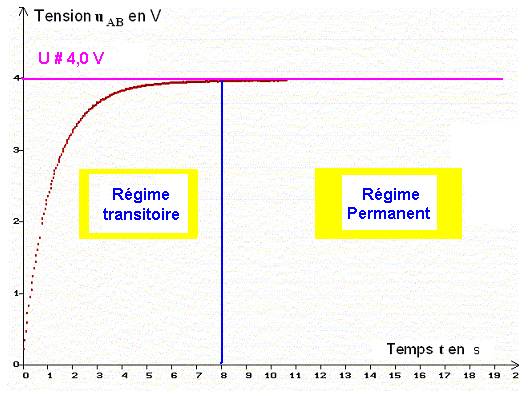
-  La courbe  u_AB = f (t)  est une fonction croissante du temps. 

-  Il existe un régime transitoire (le condensateur se charge) lorsque 0 < t < 8 s. 

-  Un régime permanent (le condensateur est chargé) lorsque t > 8 s.

-  La valeur maximale de la tension lorsque le condensateur est chargé est : U_max ≈ 4,0 V.

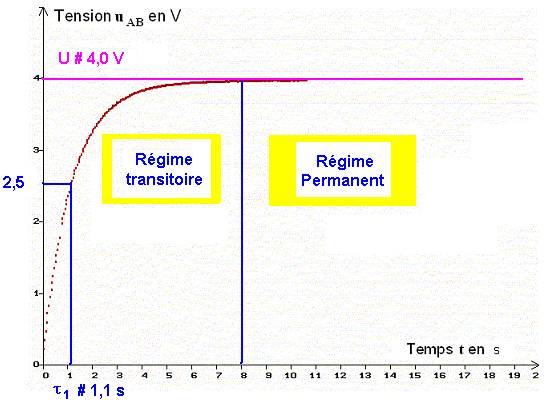
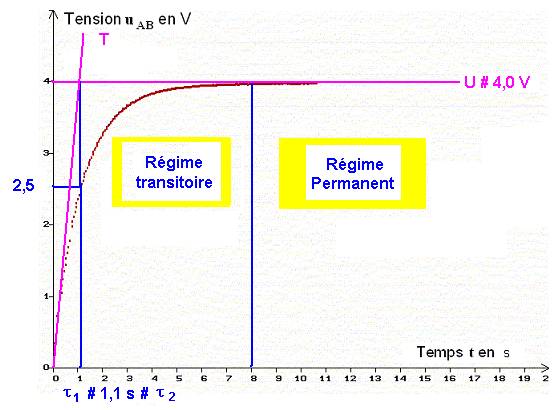
-  Valeur du produit RC : C = 1000 μF, et R =  1000 Ω,

-  Le produit RC est homogène à un temps :

-  RC = 1000 x 1000 x 10 ^{– 6}

-  RC ≈ 1,0 s 

-  De manière graphique, on trouve  : τ₁ ≈ τ ₂ ≈ 1,1 s.

-  L’erreur commise est de l’ordre de 10 %.

c)- Étude de q _AB = g(t) : sélectionner : ‚

-  Commenter la courbe obtenue. Donner ses caractéristiques. 

-  Donner la valeur de la charge Q aux bornes du condensateur lorsqu’il est chargé. 

-  (on peut utiliser l’outil : POINTEUR)

-  La courbe  q_A = g (t)  est une fonction croissante du temps. 

-  Il existe un régime transitoire (le condensateur se charge) lorsque 0 < t < 8 s. 

-  Un régime permanent (le condensateur est chargé) lorsque t > 8 s.

-  Lorsque le condensateur est chargé, Q ≈ 4,0 mC.

d)-     Étude de i = h (t) : sélectionner :

-  Commenter la courbe obtenue. Donner ses caractéristiques. 

-  Déterminer la valeur maximale I_max de l’intensité.

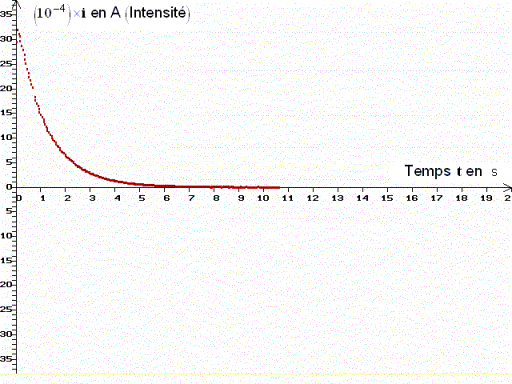
-  L’intensité est une fonction décroissante du temps. 

-  Lorsque le condensateur se charge, l’intensité du courant dans le circuit diminue et s’annule lorsque le condensateur est chargé.

-  Au temps t = 0 s, l’intensité dans le circuit est maximale est : I_max ≈ 32 x 10 ^{– 4}  A.

III- Charge et décharge d’un condensateur : si le temps le permet.

1)- Montage : c’est le même.

2)- Le Logiciel CONDO. Les connexions et les paramètres ne changent pas.

a)-     Sélectionner : (3)  Acquisitions : choisir �  : U = f (t) c’est-à-dire : u_AB = f (t).

-  Appuyer sur la lettre L de lancer et fermer l’interrupteur .

-  Lorsque le condensateur est chargé, basculer rapidement l’interrupteur pour le décharger.

-  Lorsque l’acquisition est terminée, appuyer sur la lettre M pour revenir au menu précédent.

b)-     Étude de u _AB = f(t) : sélectionner : �

-  Commenter la courbe obtenue. Donner ses caractéristiques lors de la charge et lors de la décharge.

-  document qui représente les variations de la tension u_AB en fonction du temps :

-  les deux phases de la charge ou de la décharge du condensateur : régime transitoire et régime permanent.

-  ordonnée de l’asymptote horizontale à la courbe représentant la charge du condensateur :

-  

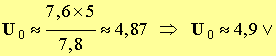
c)-     Étude de i = h(t) : sélectionner : „

-  Commenter les courbes obtenues. Donner ses caractéristiques. 

- Déterminer la valeur maximale I_max de l’intensité pour chaque cas. Conclusion.

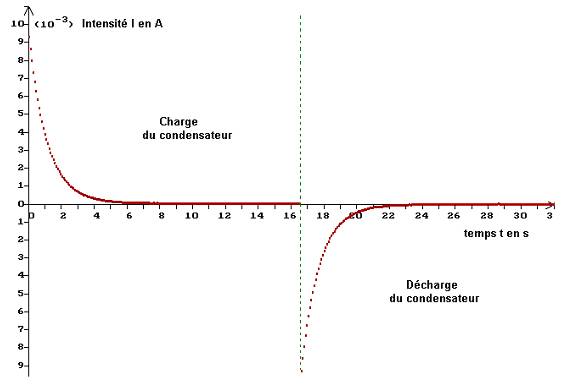
-  Lors de la charge, l’intensité du courant diminue au cours du temps pour s’annuler lorsque le condensateur est chargé.

-  Lors de la décharge, l’intensité du courant change de sens. 

-  Elle diminue en valeur absolue pour s’annuler lorsque le condensateur est déchargé. 

-  L’intensité du courant subit une discontinuée. La tension  ne subit pas de discontinuité.

IV- Les différentes courbes.

1)- Charge à courant constant.

2)- Charge à tension constante.