|
Charge d'un condensateur. Correction |
|
|
I - Présentation du condensateur. II - Charge d’un condensateur par un courant d’intensité constante. |
|
|
|
Matériel : condensateur 1000 μF, condensateur 2200 μF, conducteur ohmique 2,2 kΩ, interrupteur inverseur, plaque de connexions, générateur de tension, générateur de courant, multimètres, fils. |
I- Présentation du condensateur.
1)- Définition.
2)- Le condensateur : un dipôle qui stocke des charges électriques.
a)- Expérience 1.
- Dispositif expérimental :
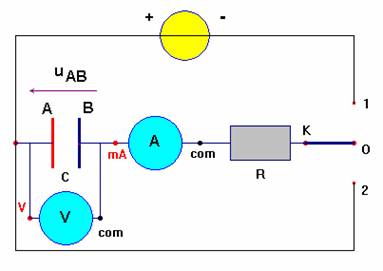
- Observation et interprétation.
b)- Expérience 2.
- Dispositif expérimental.
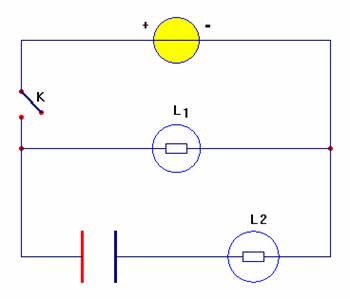
- Observation et interprétation.
II- Charge d’un condensateur par un courant d’intensité constante.
1)- But :
|
Étudier l’évolution en fonction du temps de la tension uAB à ses bornes lors de la charge à intensité constanteI0. Déterminer la valeur de la capacité C d’un condensateur. |
2)- Montage :
réaliser
le montage suivant. Le faire vérifier.
|
Attention, on utilise un condensateur électrochimique. Il est polarisé. Il faut respecter les polarités. |
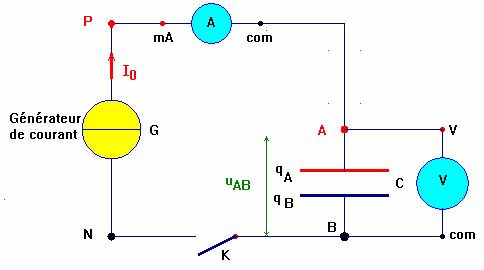
- Le générateur de courant délivre une intensité constante I0.
- Attention : le condensateur est polarisé.
Régler l’intensité du courant à l’aide du potentiomètre à
I0
≈ 200
μA.
3)- Mesures.
- Dans un premier temps, estimer la durée de la charge Δt avec le chronomètre.
- Dans un deuxième temps, décharger le condensateur, puis :
- Charger le condensateur et relever la valeur de la tension uAB toutes les x secondes afin de faire une douzaine de mesures.
|
uAB |
0 |
|
|
|
|
|
|
|
|
|
|
||
|
t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
- Noter la valeur de I0 lors de la charge.
|
- Durée de la charge : environ 1 min 30 s - On peut relever la valeur de la tension toutes les
x
= 10 s. - Valeur de l’intensité :
I0
≈ 204
μA = 0,204 mA - Remarque : Lorsque
t
> 90 s, I0
diminue
rapidement et tend vers 0. |
|
t |
uAB
V |
q
mC |
|
0,0 |
0,00 |
0,00 |
|
10 |
1,01 |
2,04 |
|
20 |
1,81 |
4,08 |
|
30 |
2,72 |
6,12 |
|
40 |
3,67 |
8,16 |
|
50 |
4,60 |
10,20 |
|
60 |
5,50 |
12,24 |
|
70 |
6,43 |
14,28 |
|
80 |
7,35 |
16,32 |
|
90 |
8,24 |
18,36 |
|
100 |
8,24 |
|
|
110 |
8,24 |
18,36 |
|
120 |
8,24 |
18,36 |
4)- Exploitation des mesures.
- Sachant qu’à courant constant, la charge Q du condensateur pendant la durée Δt est donnée par la relation : Q = I0 . Δt
- Représenter graphiquement : Q = f (uAB).
- Commenter la courbe obtenue. Rechercher le coefficient directeur de la droite moyenne et donner son unité.
Cliquer sur l'image pour l'agrandir
|
- Les points sont sensiblement alignés. La courbe moyenne passe par l’origine. - La charge est proportionnelle à l’intensité : q = k . uAB. - La constante k est le coefficient directeur de la droite tracée. - - Avec le tableur Excel, on peut faire une étude statistique des mesures : - On en déduit que : - q ≈ 2,232 . uAB => k ≈ 2,232 mC / V - Avec une bonne adéquation car R² = 0,9999 |
5)- Capacité d‘un condensateur.
- Le coefficient directeur de la droite moyenne est une grandeur caractéristique du condensateur :
- c’est la capacité du condensateur, notée C.
- Elle s’exprime en farad de symbole F.
- Le constructeur annonce une valeur pour C = 2200 μF.
- La valeur trouvée est-elle cohérente ? Justifier.
|
- Le coefficient
k représente la capacité du condensateur dont l’unité est le farad (F) dans le
S.I. - On en déduit que :
C
= k
≈ 2,232 mF = 2232
μF - Précision de la mesure : - - Le résultat est en accord avec l’indication donnée
par le constructeur. |
6)- Si le temps le permet.
- Tracer la courbe uAB = f (t). Commenter la courbe obtenue.
Cliquer sur l'image pour l'agrandir
