I- Étude  des ondes ultrasonores.

1)- Mesure de la longueur d’onde d’une onde ultrasonore.

  Réaliser le montage suivant et le faire vérifier.

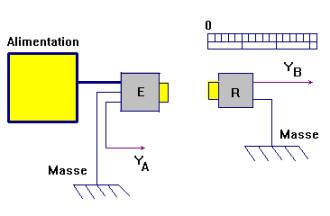
-  Réaliser les réglages afin d’obtenir un oscillogramme exploitable 

-  (il faut régler la durée de balayage pour observer une à deux périodes et la sensibilité verticale pour utiliser les 2/3  de l’écran).

-  Placer l’émetteur E et le récepteur R de façon à ce que les courbes observées à l’oscilloscope soient en phase (R doit être suffisamment proche de E). 

-  Repérer la position initiale de R. déplacer R jusqu’à ce que les courbes se trouvent en phase pour la dixième fois. 

-  On note d le déplacement correspondant du récepteur R.

Quelle relation existe-t-il entre la longueur d’onde λ et la distance d ?

       En déduire la valeur de la longueur d’onde λ de l’onde ultrasonore ?

-  Relation entre la longueur d’onde λ et la distance d. 

-  Comme les courbes sont en phase pour la dixième fois  d = 10 λ

-  Valeur du déplacement d : la mesure donne :   d » 8,8 cm

-  Longueur d’onde de l’onde ultrasonore : λ » 0,88 cm

-  Indiquer les valeurs choisies pour la durée de balayage et la sensibilité verticale.

-  Durée de balayage ou sensibilité horizontale  s = 5,0 μs / div

-  Sensibilité verticale :  Voie A :  k = 2,0 V / div et voie B :  de k = 2,0 V / div  à k = 0,50 V / div

-  Comparer l’allure des deux courbes observées lorsque R s’éloigne de E.

-  Lorsque le récepteur R s’éloigne de l’émetteur E, l’amplitude de la courbe observée à la voie B diminue. 

-  Au cours de la propagation, l’onde sonore est amortie. 

-  De l'énergie est dissipée lors de la propagation. Le récepteur ne reçoit qu’une partie de l’énergie émise par l’émetteur.

-  Déterminer la valeur de la période pour chaque onde. En déduire la valeur de la  fréquence pour chaque onde. 

-  Le constructeur indique que la fréquence de l’onde ultrasonore émise par l’émetteur est f » 40 kHz. 

-  Le résultat est-il compatible avec cette valeur ?

-  Les deux ondes ont la même période T.  

-  T = s . x

-  T = 5,0 × 4,9

-  T » 24,5 μs

-  Fréquence de l’onde ultrasonore :

- 

-  Comparaison :

-  Calculer la célérité v des ondes ultrasonores dans l’air.

- On indique que  ou T représente la température absolue du milieu. 

-  Comparer les valeurs de v et v _son. Conclusion. 

-  L’air est-il un milieu dispersif  pour les ondes sonores ?  

-  Célérité de l‘onde ultrasonore dans l’air à la température θ = 25 ° C.

-  Valeur expérimentale de la vitesse : Relation fondamentale :

- 

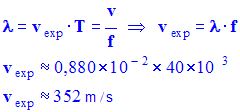
-  Valeur théorique de la vitesse à 25 ° C :

 - 

-  Comparaison :

-  La valeur expérimentale est proche de la valeur théorique. 

-  L’air n’est pas un milieu dispersif pour les ondes

2)- Diffraction des ondes ultrasonores.

  Réaliser le montage 1 :

-  Placer le récepteur R en face de l’émetteur E.

- Déplacer R sur un arc de cercle et mesurer l’amplitude du signal reçu U_m tous les 10 °. 

-  Pour des raisons de symétrie, réaliser les mesures que d’un seul côté.

-  Conclusion.

-  Les ondes ultrasonores sont des ondes directives, elles se déplacent dans un cône étroit.

  Refaire l’expérience (Montage 2) en plaçant une fente devant l’émetteur. 

  Refaire les mesures pour différentes largeurs de la fente (a = 3 cm, a = 1 cm et a = 0,5 cm).

-  Conclusion.

-  Lorsque l’ouverture est de l’ordre de grandeur de la longueur d’onde des ondes ultrasonores, l’onde est diffractée. 

-  Elle subit le phénomène de diffraction. Elle perd sa directivité.

II- Diffraction de la lumière.

1)- Dispositif expérimental. (Vue de dessus)

  Réaliser le montage précédent. Placer l’écran à la distance D = 2,50 m de la fente. 

  Placer la fente d’ouverture a connue. Régler afin d’obtenir une figure de diffraction exploitable. 

  Mesurer la largeur L de la tache centrale de diffraction pour différentes largeurs a de la fente.

2)- Résultats des mesures.

-  Tableau : reproduire et compléter le tableau suivant : 

-  Lors de l'expérience, la distance D = 2,50 m

3)- Exploitation.

-  Tracer la courbe L = f (1/a). Tracer la droite moyenne et calculer le coefficient directeur k de cette droite. Donner son unité dans le S.I.

-  En conséquence la largeur de la tache centrale est inversement proportionnelle à la largeur de la fente :

-   

- k = 320 × 10 ^{- 2} × 10 ^{- 6} m ²

- k » 3,20 × 10 ^{- 6} m ²

-  Exploitation sur le graphe papier :

-  Avec ΔL » 6,4 cm et

-  Valeur de k :  

-  Cette valeur correspond bien à la valeur donnée par le logiciel Excel qui fait une étude statistique (droite de régression).

-  Vérifier que k = 2 λ . D (longueur d’onde dans le vide pour le laser rouge : λ = 632,8 nm)

-  Calcul de k à partir de la formule :  

- k = 2 λ . D

- k = 2 × 632,8 × 10 ^{- 9} × 2,50

- k » 3,16 × 10 ^{- 6} m ²

-  On trouve :

-  On peut en déduire que :  (1)

-  On peut considérer que D >> L / 2, en conséquence ; 

-  l’angle θ (rad) est petit. On peut faire l’approximation des petits angles : tan θ » θ. En déduire la relation liant θ (rad), λ et a.

-  D’autre part :  (2)

-  Comme D >> a, on peut utiliser l’approximation suivante : (3) tan θ » θ.

-  En combinant (1), (2) et (3), on trouve :